ДОНЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к отчету по НИРС на тему
«Применение нейросетей в автоматизации»
Проверил д.т.н., профессор Коцегуб П.Х.
Донецк 1999
РЕФЕРАТ
30 с., 14 рис., 0 табл., 0 приложений, 2 источника.
Объектом исследований данной работы является тиристорный электропривод постоянного тока.
Цель работы – синтез нейроконтроллера, обеспечивающего корректную работу системы регулирования скорости независимо от параметров электропривода, проверка эффективности функционирования разработанных узлов.
Исследования выполнялись на основе теории управления электроприводами, для исследования разработанных схем использовался метод математического моделирования на персональном компьютере с применением программного пакета Matlab 5.3 и приложения Simulink 3.0, предназначенного для моделирования динамических систем.
В результате работы синтезирована систем регулирования скорости спомощью нейроконтроллера ,проанализировано функционирование исследуемой системы при разгоне от задатчика интенсивности. Проведенное моделирование разработанной системы показало эффективность функционирования нейроконтроллера.
ТИРИСТОРНЫЙ ЭЛЕКТРОПРИВОД ПОСТОЯННОГО ТОКА, НЕЙРОКОНТРОЛЛЕР,
ЗАДАТЧИК ИНТЕНСИВНОСТИ, ОБРАТНОЕ РАСПРОСТРАНЕНИЕ ОШИБКИ, ГЕНЕТИЧЕСКИЙ АЛГОРИТМ,
МАТРИЦА ВЕСОВ, АКТИВАЦИОННАЯ ФУНКЦИЯ
СОДЕРЖАНИЕ
Перечень условных обозначений и сокращений
Введение 1Основы
искусственных нейронных сетей 2Процедура
обратного распространения 2.1
Обучающий алгоритм обратного распространения 2.2
Многослойная сеть 3Системы
регулирования скорости в схеме ТП–Д с нейроконтроллером
Заключение Перечень ссылок
Перечень условных обозначений и сокращений ЗИ – задатчик интенсивности;
МР – модальный регулятор;
ТП-Д – тиристорный преобразователь – двигатель;
ТП – тиристорный преобразователь;
а.е. – абсолютные единицы;
о.е. – относительные единицы.
C – конструктивная постоянная двигателя;
ЕД – ЭДС двигателя;
EП – ЭДС преобразователя;
I – ток якорной цепи;
IКЗ, MКЗ – ток и момент короткого
замыкания;
M, MC – электромагнитный и статический
моменты;
RЯ – активное сопротивление якорной
цепи системы ТП-Д;
TЯ, TM – электромагнитная
и электромеханическая постоянные времени привода;
W(p) – передаточная функция;
k1a, k2a, k3a
– коэффициенты МР;
kП, T? – коэффициент усиления
и постоянная времени ТП;
uБ, yБ – базовые значения
входной и выходной величин;
y*, u* – выходная и входная
величины в относительных единицах;
? – угловая скорость двигателя;
?0, E0 – скорость и ЭДС в
режиме холостого хода; S?
суммирующий блок; W - маттрица весов; X – входная матрица нейроконтроллера; Y
– выходная матрица нейроконтроллера; NET –
выход суммирующего блока; OUT
– выход нейрона; F(x)
– активационная функция; $ - покомпонентное произведение векторов; ?
- коэффициент скорости обучения, служащий для управления средней величиной
изменения веса.
ВВЕДЕНИЕ После двух десятилетий почти полного забвения интерес
к искусственным нейронным сетям быстро вырос за последние несколько лет.
Специалисты из таких далеких областей, как техническое конструирование,
философия, физиология и психология, заинтригованы возможностями, предоставляемыми
этой технологией, и ищут приложения им внутри своих дисциплин.
Это возрождение интереса было вызвано как теоретическими,
так и прикладными достижениями. Неожиданно открылись возможности использования
вычислений в сферах, до этого относящихся лишь к области человеческого
интеллекта, возможности создания машин, способность которых учиться и запоминать
удивительным образом напоминает мыслительные процессы человека, и наполнения
новым значительным содержанием критиковавшегося термина “искусственный
интеллект”.
Искусственные нейронные сети индуцированы биологией,
так как они состоят из элементов, функциональные возможности которых аналогичны
большинству элементарных функций биологического нейрона. Эти элементы затем
организуются по способу, который может соответствовать (или не соответствовать)
анатомии мозга. Несмотря на такое поверхностное сходство, искусственные
нейронные сети демонстрируют удивительное число свойств присущих мозгу.
Например, они обучаются на основе опыта, обобщают предыдущие прецеденты
на новые случаи и извлекают существенные свойства из поступающей информации,
содержащей излишние данные.
Несмотря на такое функциональное сходство, даже
самый оптимистичный их защитник не предположит, что в скором будущем искусственные
нейронные сети будут дублировать функции человеческого мозга. Реальный
“интеллект”, демонстрируемый самыми сложными нейронными сетями, находится
ниже уровня дождевого червя, и энтузиазм должен быть умерен в соответствии
с современными реалиями. Однако равным образом было бы неверным игнорировать
удивительное сходство в функционировании некоторых нейронных сетей с человеческим
мозгом. Эти возможности, как бы они ни были ограничены сегодня, наводят
на мысль, что глубокое проникновение в человеческий интеллект, а также
множество революционных приложений, могут быть не за горами.
Людей всегда интересовало их собственное мышление.
Это самовопрошение, думание мозга о себе самом является, возможно, отличительной
чертой человека. Имеется множество размышлений о природе мышления, простирающихся
от духовных до анатомических. Обсуждение этого вопроса, протекавшее в горячих
спорах философов и теологов с физиологами и анатомами, принесло мало пользы,
так как сам предмет весьма труден для изучения. Те, кто опирался на самоанализ
и размышление, пришли к выводам, не отвечающим уровню строгости физических
наук. Экспериментаторы же нашли, что мозг труден для наблюдения и ставит
в тупик своей организацией. Короче говоря, мощные методы научного исследования,
изменившие наш взгляд на физическую реальность, оказались бессильными в
понимании самого человека.
Нейробиологи и нейроанатомы достигли значительного
прогресса. Усердно изучая структуру и функции нервной системы человека,
они многое поняли в “электропроводке” мозга , но мало узнали о его функционировании.
В процессе накопления ими знаний выяснилось, что мозг имеет ошеломляющую
сложность. Сотни миллиардов нейронов, каждый из которых соединен с сотнями
или тысячами других, образуют систему, далеко превосходящую наши самые
смелые мечты о суперкомпьютерах. Тем не менее мозг постепенно выдает свои
секреты в процессе одного из самых напряженных и честолюбивых исследований
в истории человечества.
Лучшее понимание функционирования нейрона и картины
его связей позволило исследователям создать математические модели для проверки
своих теорий. Эксперименты теперь могут проводиться на цифровых компьютерах
без привлечения человека или животных, что решает многие практические и
морально-этические проблемы. В первых же работах выяснилось, что эти модели
не только повторяют функции мозга, но и способны выполнять функции, имеющие
свою собственную ценность. Поэтому возникли и остаются в настоящее время
две взаимно обогащающие друг-друга цели нейронного моделирования: первая
– понять функционирование нервной системы человека на уровне физиологии
и психологии и вторая – создать вычислительные системы (искусственные нейронные
сети), выполняющие функции, сходные с функциями мозга. Именно эта последняя
цель и находится в центре внимания этой книги.
Параллельно с прогрессом в нейроанатомии и нейрофизиологии
психологами были созданы модели человеческого обучения. Одной из таких
моделей, оказавшейся наиболее плодотворной, была модель Д. Хэбба, который
в 1949г. предложил закон обучения, явившийся стартовой точкой для алгоритмов
обучения искусственных нейронных сетей. Дополненный сегодня множеством
других методов он продемонстрировал ученым того времени, как сеть нейронов
может обучаться.
В пятидесятые и шестидесятые годы группа исследователей,
объединив эти биологические и физиологические подходы, создала первые искусственные
нейронные сети. Выполненные первоначально как электронные сети, они были
позднее перенесены в более гибкую среду компьютерного моделирования, сохранившуюся
и в настоящее время. Первые успехи вызвали взрыв активности и оптимизма.
Минский, Розенблатт, Уидроу и другие разработали сети, состоящие из одного
слоя искусственных нейронов. Часто называемые персептронами, они были использованы
для такого широкого класса задач, как предсказание погоды, анализ электрокардиограмм
и искусственное зрение. В течение некоторого времени казалось, что ключ
к интеллекту найден и воспроизведение человеческого мозга является лишь
вопросом конструирования достаточно большой сети.
Но эта иллюзия скоро рассеялась. Сети не могли
решать задачи, внешне весьма сходные с теми, которые они успешно решали.
С этих необъяснимых неудач начался период интенсивного анализа. Минский,
используя точные математические методы, строго доказал ряд теорем, относящихся
к функционированию сетей.
Его исследования привели к написанию книги, в которой
он вместе с Пайпертом доказал, что используемые в то время однослойные
сети теоретически неспособны решить многие простые задачи, в том числе
реализовать функцию “Исключающее ИЛИ”. Минский также не был оптимистичен
относительно потенциально возможного здесь прогресса:
Персептрон показал себя заслуживающим изучения,
несмотря на жесткие ограничения (и даже благодаря им). У него много привлекательных
свойств: линейность, занимательная теорема об обучении, простота модели
параллельных вычислений. Нет оснований полагать, что эти достоинства сохраняться
при переходе к многослойным системам. Тем не менее мы считаем важной задачей
для исследования подкрепление (или опровержение) нашего интуитивного убеждения,
что такой переход бесплоден.
Возможно, будет открыта какая-то мощная теорема
о сходимости или найдена глубокая причина неудач дать интересную “теорему
обучения” для многослойных машин.
Блеск и строгость аргументации Минского, а также
его престиж породили огромное доверие к книге – ее выводы были неуязвимы.
Разочарованные исследователи оставили поле исследований ради более обещающих
областей, а правительства перераспределили свои субсидии, и искусственные
нейронные сети были забыты почти на два десятилетия.
Тем не менее несколько наиболее настойчивых ученых,
таких как Кохонен, Гроссберг, Андерсон продолжили исследования. Наряду
с плохим финансированием и недостаточной оценкой ряд исследователей испытывал
затруднения с публикациями. Поэтому исследования, опубликованные в семидесятые
и начале восьмидесятых годов, разбросаны в массе различных журналов, некоторые
из которых малоизвестны. Постепенно появился теоретический фундамент, на
основе которого сегодня конструируются наиболее мощные многослойные сети.
Оценка Минского оказалась излишне пессимистичной, многие из поставленных
в его книге задач решаются сейчас сетями с помощью стандартных процедур.
За последние несколько лет теория стала применяться
в прикладных областях и появились новые корпорации, занимающиеся коммерческим
использованием этой технологии. Нарастание научной активности носило взрывной
характер. В 1987 г. было проведено четыре крупных совещания по искусственным
нейронным сетям и опубликовано свыше 500 научных сообщений – феноменальная
скорость роста.
Урок, который можно извлечь из этой истории, выражается
законом Кларка, выдвинутым писателем и ученым Артуром Кларком. В нем утверждается,
что, если крупный уважаемый ученый говорит, что нечто может быть выполнено,
то он (или она) почти всегда прав. Если же ученый говорит, что это не может
быть выполнено, то он (или она) почти всегда не прав. История науки является
летописью ошибок и частичных истин. То, что сегодня не подвергается сомнениям,
завтра отвергается. Некритическое восприятие “фактов” независимо от их
источника может парализовать научный поиск. С одной стороны, блестящая
научная работа Минского задержала развитие искусственных нейронных сетей.
Нет сомнений, однако, в том, что область пострадала вследствие необоснованного
оптимизма и отсутствия достаточной теоретической базы. И возможно, что
шок, вызванный книгой “Персептроны”, обеспечил необходимый для созревания
этой научной области период.
1ОСНОВЫ ИСКУССТВЕННЫХ НЕЙРОННЫХ
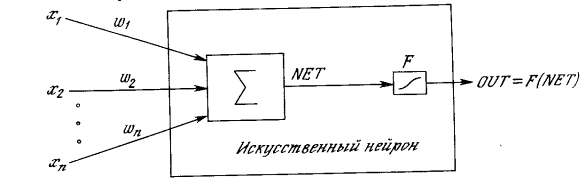
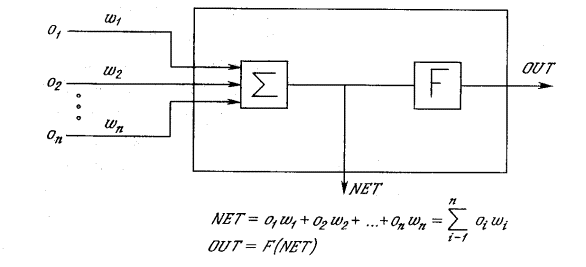
СЕТЕЙ Искусственный нейрон имитирует в первом приближении
свойства биологического нейрона. На вход искусственного нейрона поступает
некоторое множество сигналов, каждый из которых является выходом другого
нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической
силе, и все произведения суммируются, определяя уровень активации нейрона.
Хотя сетевые парадигмы весьма разнообразны, в основе почти всех их лежит
эта конфигурация. Здесь множество входных сигналов, обозначенных x1, x2,…, xn,
поступает на искусственный нейрон. Эти входные сигналы, в совокупности
обозначаемые вектором X, соответствуют сигналам, приходящим в синапсы биологического
нейрона. Каждый сигнал умножается на соответствующий вес w1, w2,…,wn,
и поступает на суммирующий блок, обозначенный ?.
Каждый вес соответствует “силе” одной биологической синаптической связи.
(Множество весов в совокупности обозначается вектором W.) Суммирующий блок,
соответствующий телу биологического элемента, складывает взвешенные входы
алгебраически, создавая выход, который мы будем называть NET.
В векторных обозначениях это может быть компактно записано следующим образом:
NET = XW.(1.1)
Сигнал NET
далее, как правило, преобразуется активационной функцией F и дает выходной
нейронный сигнал OUT.
Активационная функция может быть обычной линейной функцией
OUT = K(NET),(1.2)
где К – постоянная, пороговой функции
OUT = 1, если
NET > T (1.3)
OUT
= 0 в остальных случаях,
где Т – некоторая постоянная пороговая величина,
или же функцией, более точно моделирующей нелинейную передаточную характеристику
биологического нейрона и представляющей нейронной сети большие возможности.
Рисунок 1.2 – Искусственный нейрон с активационной
функцией На рис. 1.2 блок, обозначенный F,
принимает сигнал NET
и выдает сигнал OUT.
Если блок F сужает диапазон изменения величины NET
так, что при любых значениях NET
значения OUT
принадлежат некоторому конечному интервалу, то F называется “сжимающей”
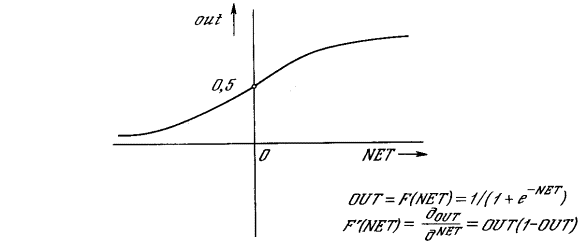
функцией. В качестве “сжимающей” функции часто используется логистическая
или “сигмоидальная” (S-образная) функция, показанная на рис. 1.3а. Эта
функция математически выражается как F(x)
= 1/(1 + е-x).
Таким образом,
По аналогии с электронными системами активационную
функцию можно считать нелинейной усилительной характеристикой искусственного
нейрона. Коэффициент усиления вычисляется как отношение приращения величины OUT
к вызвавшему его небольшому приращению величины NET.
Он выражается наклоном кривой при определенном уровне возбуждения и изменяется
от малых значений при больших отрицательных возбуждениях (кривая почти
горизонтальна) до максимального значения при нулевом возбуждении и снова
уменьшается, когда возбуждение становится большим положительным. Гроссберг
(1973) обнаружил, что подобная нелинейная характеристика решает поставленную
им дилемму шумового насыщения. Каким образом одна и та же сеть может обрабатывать
как слабые, так и сильные сигналы? Слабые сигналы нуждаются в большом сетевом
усилении, чтобы дать пригодный к использованию выходной сигнал. Однако
усилительные каскады с большими коэффициентами усиления могут привести
к насыщению выхода шумами усилителей (случайными флуктуациями), которые
присутствуют в любой физически реализованной сети. Сильные входные сигналы
в свою очередь также будут приводить к насыщению усилительных каскадов,
исключая возможность полезного использования выхода. Центральная область
логистической функции, имеющая большой коэффициент усиления, решает проблему
обработки слабых сигналов, в то время как области с падающим усилением
на положительном и отрицательном концах подходят для больших возбуждений.
Таким образом, нейрон функционирует с большим усилением в широком диапазоне
уровня входного сигнала.
а) Другой широко используемой активационной функцией
является гиперболический тангенс. По форме она сходна с логистической функцией
и часто используется биологами в качестве математической модели активации
нервной клетки. В качестве активационной функции искусственной нейронной
сети она записывается следующим образом:
OUT = th(x).(1.5)
б) Рисунок 1.3 – Активационные функции:
Подобно логистической функции гиперболический тангенс
является S-образной функцией, но он симметричен относительно начала координат,
и в точке NET
= 0 значение выходного сигнала OUT
равно нулю (см. рис. 1.3б). В отличие от логистической функции гиперболический
тангенс принимает значения различных знаков, что оказывается выгодным для
ряда сетей.
Рассмотренная простая модель искусственного нейрона
игнорирует многие свойства своего биологического двойника. Например, она
не принимает во внимание задержки во времени, которые воздействуют на динамику
системы. Входные сигналы сразу же порождают выходной сигнал. И, что более
важно, она не учитывает воздействий функции частотной модуляции или синхронизирующей
функции биологического нейрона, которые ряд исследователей считают решающими.
Несмотря на эти ограничения, сети, построенные
из этих нейронов, обнаруживают свойства, сильно напоминающие биологическую
систему. Только время и исследования смогут ответить на вопрос, являются
ли подобные совпадения случайными или следствием того, что в модели верно
схвачены важнейшие черты биологического нейрона.
Хотя один нейрон и способен выполнять простейшие
процедуры распознавания, сила нейронных вычислений проистекает от соединений
нейронов в сетях.
Рисунок 1.5 – Двухслойная нейронная сеть Многослойные сети могут образовываться каскадами
слоев. Выход одного слоя является входом для последующего слоя. Подобная
сеть показана на рис. 1.5 и снова изображена со всеми соединениями.
Многослойные сети не могут привести к увеличению
вычислительной мощности по сравнению с однослойной сетью лишь в том случае,
если активационная функция между слоями будет нелинейной. Вычисление выхода
слоя заключается в умножении входного вектора на первую весовую матрицу
с последующим умножением (если отсутствует нелинейная активационная функция)
результирующего вектора на вторую весовую матрицу.
(XW1)W2
Так как умножение матриц ассоциативно, то
X(W1W2).
Это показывает, что двухслойная линейная сеть эквивалентна
одному слою с весовой матрицей, равной произведению двух весовых матриц.
Следовательно, любая многослойная линейная сеть может быть заменена эквивалентной
однослойной сетью. Таким образом, для расширения возможностей сетей по
сравнению с однослойной сетью необходима нелинейная активационная функция.
У сетей, рассмотренных до сих пор, не было обратных
связей, т. е. соединений, идущих от выходов некоторого слоя к входам этого
же слоя или предшествующих слоев. Этот специальный класс сетей, называемых
сетями без обратных связей или сетями прямого распространения, представляет
интерес и широко используется. Сети более общего вида, имеющие соединения
от выходов к входам, называются сетями с обратными связями. У сетей без
обратных связей нет памяти, их выход полностью определяется текущими входами
и значениями весов. В некоторых конфигурациях сетей с обратными связями
предыдущие значения выходов возвращаются на входы; выход, следовательно,
определяется как текущим входом, так и предыдущими выходами. По этой причине
сети с обратными связями могут обладать свойствами, сходными с кратковременной
человеческой памятью, сетевые выходы частично зависят от предыдущих входов.
2Процедура обратного распространения Долгое время не было теоретически обоснованного
алгоритма для обучения многослойных искусственных нейронных сетей. А так
как возможности представления с помощью однослойных нейронных сетей оказались
весьма ограниченными, то и вся область в целом пришла в упадок.
Разработка алгоритма обратного распространения
сыграла важную роль в возрождении интереса к искусственным нейронным сетям.
Обратное распространение – это систематический метод для обучения многослойных
искусственных нейронных сетей. Он имеет солидное математическое обоснование.
Несмотря на некоторые ограничения, процедура обратного распространения
сильно расширила область проблем, в которых могут быть использованы искусственные
нейронные сети, и убедительно продемонстрировала свою мощь.
Рисунок 2.1 – Искусственный нейрон с активационнной функцией На рис. 2.1 показан нейрон, используемый в качестве
основного строительного блока в сетях обратного распространения. Подается
множество входов, идущих либо извне, либо от предшествующего слоя. Каждый
из них умножается на вес, и произведения суммируются. Эта сумма, обозначаемая NET,
должна быть вычислена для каждого нейрона сети. После того, как величина NET
вычислена, она модифицируется с помощью активационной функции и получается
сигнал OUT.
Рисунок 2.2 – Сигмоидальная активационная функция На рис. 2.2 показана активационная функция, обычно
используемая для обратного распространения.
Как показывает уравнение (2.2), эта функция, называемая
сигмоидом, весьма удобна, так как имеет простую производную, что используется
при реализации алгоритма обратного распространения.
Сигмоид, который иногда называется также логистической,
или сжимающей функцией, сужает диапазон изменения NET
так, что значение OUT
лежит между нулем и единицей. Как указывалось выше, многослойные нейронные
сети обладают большей представляющей мощностью, чем однослойные, только
в случае присутствия нелинейности. Сжимающая функция обеспечивает требуемую
нелинейность.
В действительности имеется множество функций, которые
могли бы быть использованы. Для алгоритма обратного распространения требуется
лишь, чтобы функция была всюду дифференцируема. Сигмоид удовлетворяет этому
требованию. Его дополнительное преимущество состоит в автоматическом контроле
усиления. Для слабых сигналов (величина NET
близка к нулю) кривая вход-выход имеет сильный наклон, дающий большое усиление.
Когда величина сигнала становится больше, усиление падает. Таким образом,
большие сигналы воспринимаются сетью без насыщения, а слабые сигналы проходят
по сети без чрезмерного ослабления.
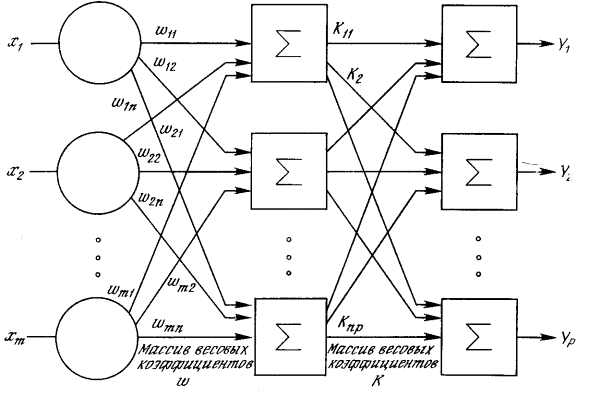
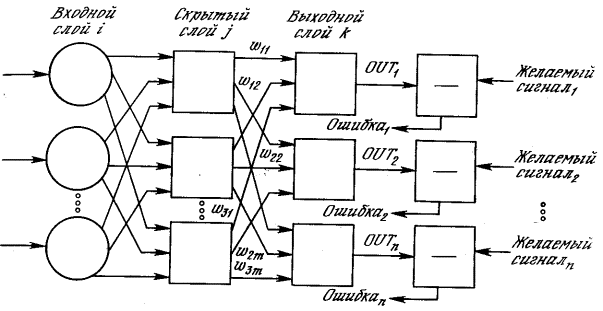
2.2 Многослойная сеть На рис. 2.3 изображена многослойная сеть, которая
может обучаться с помощью процедуры обратного распространения. Первый слой
нейронов (соединенный с входами) служит лишь в качестве распределительных
точек, суммирования входов здесь не производится. Входной сигнал просто
проходит через них к весам на их выходах. А каждый нейрон последующих слоев
выдает сигналы NET
и OUT, как
описано выше.
Рисунок 2.3 – Двухслойная сеть обратного распространения
В литературе нет единообразия относительно того,
как считать число слоев в таких сетях. Одни авторы используют число слоев
нейронов (включая несуммирующий входной слой), другие – число слоев весов.
Так как последнее определение функционально описательное, то оно будет
использоваться на протяжении книги. Согласно этому определению, сеть на
рис. 2.3 рассматривается как двухслойная. Нейрон объединен с множеством
весов, присоединенных к его входу. Таким образом, веса первого слоя оканчиваются
на нейронах первого слоя. Вход распределительного слоя считается нулевым
слоем.
Процедура обратного распространения применима к
сетям с любым числом слоев. Однако для того, чтобы продемонстрировать алгоритм,
достаточно двух слоев. Сейчас будут рассматриваться лишь сети прямого действия,
хотя обратное распространение применимо и к сетям с обратными связями.
Эти случаи будут рассмотрены в данной главе позднее.
Целью обучения сети является такая подстройка ее
весов, чтобы приложение некоторого множества входов приводило к требуемому
множеству выходов. Для краткости эти множества входов и выходов будут называться
векторами. При обучении предполагается, что для каждого входного вектора
существует парный ему целевой вектор, задающий требуемый выход. Вместе
они называются обучающей парой. Как правило, сеть обучается на многих парах.
Например, входная часть обучающей пары может состоять из набора нулей и
единиц, представляющего двоичный образ некоторой буквы алфавита.
Перед началом обучения всем весам должны быть присвоены
небольшие начальные значения, выбранные случайным образом. Это гарантирует,
что в сети не произойдет насыщения большими значениями весов, и предотвращает
ряд других патологических случаев. Например, если всем весам придать одинаковые
начальные значения, а для требуемого функционирования нужны неравные значения,
то сеть не сможет обучиться.
Обучение сети обратного распространения требует
выполнения следующих операций:
Выбрать очередную обучающую пару из обучающего
множества; подать входной вектор на вход сети.
Вычислить выход сети.
Вычислить разность между выходом сети и требуемым
выходом (целевым вектором обучающей пары).
Подкорректировать веса сети так, чтобы минимизировать
ошибку.
Повторять шаги с 1 по 4 для каждого вектора обучающего
множества до тех пор, пока ошибка на всем множестве не достигнет приемлемого
уровня.
Операции, выполняемые шагами 1 и 2, сходны с теми,
которые выполняются при функционировании уже обученной сети, т. е. подается
входной вектор и вычисляется получающийся выход. Вычисления выполняются
послойно. На рис. 2.3 сначала вычисляются выходы нейронов слояj,
затем они используются в качестве входов слоя k,
вычисляются выходы нейронов слоя k, которые и образуют выходной вектор
сети.
На шаге 3 каждый из выходов сети, которые на рис.
2.3 обозначены OUT,
вычитается из соответствующей компоненты целевого вектора, чтобы получить
ошибку. Эта ошибка используется на шаге4
для коррекции весов сети, причем знак и величина изменений весов определяются
алгоритмом обучения (см. ниже).
После достаточного числа повторений этих четырех
шагов разность между действительными выходами и целевыми выходами должна
уменьшиться до приемлемой величины, при этом говорят, что сеть обучилась.
Теперь сеть используется для распознавания и веса не изменяются.
На шаги 1 и 2 можно смотреть как на «проход вперед»,
так как сигнал распространяется по сети от входа к выходу. Шаги 3, 4 составляют
«обратный
проход», здесь вычисляемый сигнал ошибки распространяется обратно по сети
и используется для подстройки весов. Эти два прохода теперь будут детализированы
и выражены в более математической форме.
Проход вперед. Шаги 1 и 2 могут быть выражены в
векторной форме следующим образом: подается входной вектор Х и на выходе
получается вектор Y.
Векторная пара вход-цель Х и Т берется из обучающего множества. Вычисления
проводятся над вектором X, чтобы получить выходной вектор Y.
Как мы видели, вычисления в многослойных сетях
выполняются слой за слоем, начиная с ближайшего к входу слоя. Величина NET
каждого нейрона первого слоя вычисляется как взвешенная сумма входов нейрона.
Затем активационная функция F
«сжимает» NET
и дает величину OUT
для каждого нейрона в этом слое. Когда множество выходов слоя получено,
оно является входным множеством для следующего слоя. Процесс повторяется
слой за слоем, пока не будет получено заключительное множество выходов
сети.
Этот процесс может быть выражен в сжатой форме
с помощью векторной нотации. Веса между нейронами могут рассматриваться
как матрица W.
Например, вес от нейрона8
в слое2 к нейрону5
слоя3 обозначается w8,5.
Тогда NET-вектор слоя N может быть выражен не как сумма произведений, а
как произведение Х и W. В векторном обозначении N = XW.
Покомпонентным применением функции F к NET-вектору N получается выходной
вектор О. Таким образом, для данного слоя вычислительный процесс описывается
следующим выражением:
О = F(XW).(2.3)
Выходной вектор одного слоя является входным вектором
для следующего, поэтому вычисление выходов последнего слоя требует применения
уравнения (2.3) к каждому слою от входа сети к ее выходу.
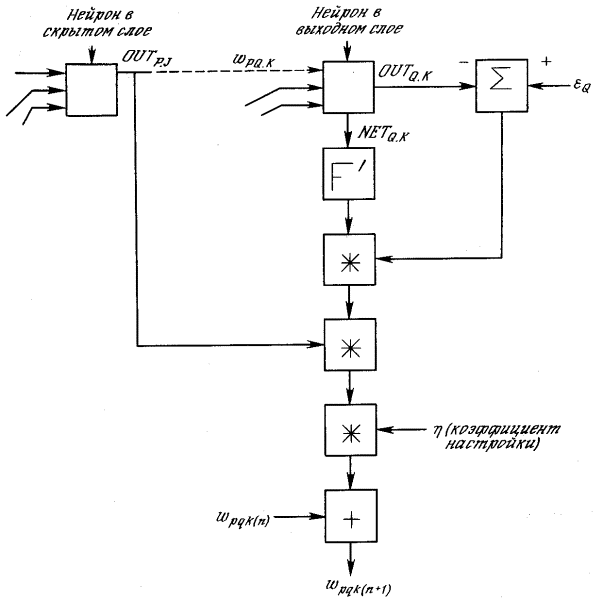
Обратный проход. Подстройка весов выходного слоя.
Так как для каждого нейрона выходного слоя задано целевое значение, то
подстройка весов легко осуществляется с использованием модифицированного
дельта-правила. Внутренние слои называют «скрытыми слоями», для их выходов
не имеется целевых значений для сравнения. Поэтому обучение усложняется.
На рис. 2.5 показан процесс обучения для одного
веса от нейрона р в скрытом слое j
к нейрону q
в выходном слое k.
Выход нейрона слоя k,
вычитаясь из целевого значения (Target),
дает сигнал ошибки. Он умножается на производную сжимающей функции [OUT(1
– OUT)], вычисленную
для этого нейрона слоя k, давая, таким образом, величину ?.
? = OUT(1
– OUT)(Target – OUT)(2.4)
Затем ?
умножается на величину OUT
нейрона j, из которого выходит рассматриваемый вес. Это произведение в
свою очередь умножается на коэффициент скорости обучения ?
(обычно от 0,01 до 1,0), и результат прибавляется к весу. Такая же процедура
выполняется для каждого веса от нейрона скрытого слоя к нейрону в выходном
слое.
Следующие уравнения иллюстрируют это вычисление:
?wpq,k
= ? ?q,k OUT(2.5)
wpq,k(n+1)
= wpq,k(n) + ?wpq,k(2.6)
где wpq,k(n) – величина веса от нейрона p
в скрытом слое к нейрону q
в выходном слое на шаге n (до коррекции); отметим, что индекс k относится
к слою, в котором заканчивается данный вес, т. е., согласно принятому в
этой книге соглашению, с которым он объединен; wpq,k(n+1) –
величина веса на шаге n
+ 1 (после коррекции); ?q,k–величина ?
для нейрона q, в выходном слое k; OUTp,j
– величина OUT
для нейрона р в скрытом слое j.
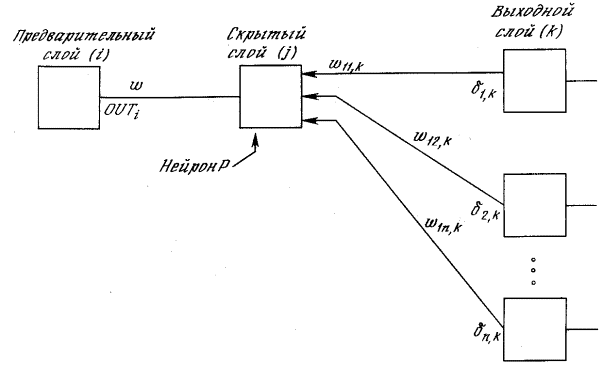
Подстройка весов скрытого слоя. Рассмотрим один
нейрон в скрытом слое, предшествующем выходному слою. При проходе вперед
этот нейрон передает свой выходной сигнал нейронам в выходном слое через
соединяющие их веса. Во время обучения эти веса функционируют в обратном
порядке, пропуская величину ?
от выходного слоя назад к скрытому слою. Каждый из этих весов умножается
на величину ?
нейрона, к которому он присоединен в выходном слое. Величина ?,
необходимая для нейрона скрытого слоя, получается суммированием всех таких
произведений и умножением на производную сжимающей функции:
(см. рис. 2.6). Когда значение ?
получено, веса, питающие первый скрытый уровень, могут быть подкорректированы
с помощью уравнений (2.5) и (2.6), где индексы модифицируются в соответствии
со слоем.
Рисунок2.5
– Настройка веса в выходном слое .Для каждого нейрона в данном скрытом слое должно
быть вычислено ? и подстроены все веса, ассоциированные с этим слоем. Этот
процесс повторяется слой за слоем по направлению к входу, пока все веса
не будут подкорректированы.
С помощью векторных обозначений операция обратного
распространения ошибки может быть записана значительно компактнее. Обозначим
множество величин ? выходного слоя через Dk
и множество весов выходного слоя как массив Wk.
Чтобы получить Dj,?-вектор
выходного слоя, достаточно следующих двух операций:
Умножить о-вектор выходного слоя Dk
на транспонированную матрицу весов W’k Умножить каждую компоненту полученного произведения
на производную сжимающей функции соответствующего нейрона в скрытом слое.
Рисунок2.6
– Настройка веса в скрытом слое В символьной записи
Dj
= DkW’k $[0j $(I – 0j)],(2.8)
где оператор $ обозначает покомпонентное произведение
векторов, Оj
– выходной вектор слоя j
и I – вектор,
все компоненты которого равны 1.
Добавление нейронного смещения. Во многих случаях
желательно наделять каждый нейрон обучаемым смещением. Это позволяет сдвигать
начало отсчета логистической функции, давая эффект, аналогичный подстройке
порога персептронного нейрона, и приводит к ускорению процесса обучения.
Эта возможность может быть легко введена в обучающий алгоритм с помощью
добавляемого к каждому нейрону веса, присоединенного к +1. Этот вес обучается
так же, как и все остальные веса, за исключением того, что подаваемый на
него сигнал всегда равен +1, а не выходу нейрона предыдущего слоя.
Метод ускорения обучения для алгоритма обратного
распространения, увеличивающий также устойчивость процесса, названный импульсом,
заключается в добавлении к коррекции веса члена, пропорционального величине
предыдущего изменения веса. Как только происходит коррекция, она «запоминается»
и служит для модификации всех последующих коррекций.Уравнения
коррекции модифицируются следующим образом:
?wpq,k(n+1)=
? ?q,k OUTp,j + a?wpq,k(n)(2.9)
wpq,k(n+1)
= wpq,k(n) + ?wpq,k(n+1)(2.10)
где (a
– коэффициент импульса, обычно устанавливается около 0,9.
Используя метод импульса, сеть стремится идти по
дну узких оврагов поверхности ошибки (если таковые имеются), а не двигаться
от склона к склону. Этот метод, по-видимому, хорошо работает на некоторых
задачах, но дает слабый или даже отрицательный эффект на других.
Сходный метод, основанный на экспоненциальном сглаживании,
который может иметь преимущество в ряде приложений:
?wpq,k(n+1)=
(1-a)
?q,k OUTp,j + a?wpq,k(n)(2.9)
Затем вычисляется изменение веса
wpq,k(n+1)
= wpq,k(n) + ??wpq,k(n+1),(2.10)
где a
коэффициент сглаживания, варьируемый и диапазоне от 0,0 до 1,0. Если a
равен 1,0, то новая коррекция игнорируется и повторяется предыдущая. В
области между 0 и 1 коррекция веса сглаживается величиной, пропорциональной a.
По-прежнему, ?
является коэффициентом скорости обучения, служащим для управления средней
величиной изменения веса.
3СИСТЕМЫ РЕГУЛИРОВАНИЯ СКОРОСТИ
В качестве базовой была принята система регулирования
скорости по схеме “тиристорный преобразователь – двигатель” с модальным
регулятором без компенсации противоЭДС, работающая от задатчика интенсивности
ЗИ. Сам модальный регулятор (в дальнейшем МР) был рассчитан при помощи
распределения Баттерворта. Схема ТП-Д-МР представлена на рис.3.1. Переходные
процессы, реализуемые этой схемой, приведены на рис.3.2.
Рисунок 3.1-Система ТП-Д-МР Таким образом, нейроконтроллер должен заставить
систему без регуляторов реализовать такие же переходные процессы, как и
система ТП-Д с МР.
В качестве входной матрицы нейроконтроллера используем
сигнал задания на скорость, а также сигналы обратных связей по трем координатам
системы-скорости двигателя, тока якоря двигателя и выходной ЭДС преобразователя.
Так как мы используем в качестве обучающего алгоритма
алгоритм обратного распространения ошибки, нам также необходимо знать выходную
матрицу нейроконтроллера (т.е. напряжение задания, поступающее на ТП).
Ее мы берем из разомкнутой системы ТП-Д-МР.
На вход нейроконтроллера поступает четыре координаты
(т.е. четыре входа), поэтому во входном слое нейроконтроллера ставим четыре
нейрона. Выход из нейроконтроллера только один, поэтому в выходном слое
нейроконтроллера ставим один нейрон.
Рисунок 3.2 – Переходные процессы в системе ТП-Д-МР
Для более точной реализации переходных процессов
в скрытом слое нейроконтроллера ставим десять нейронов.
В качестве активационных функций выбираем:для первого
слоя-logsig(x);
для скрытого слоя-tansig(x);
для выходного слоя-purelin(x).
Построенный таким образом нейроконтроллер тренируем
с помощью алгоритма обратного распространения ошибки. Критерием тренировки
служит минимум интегрально-квадратичной ошибки. Вид изменения ошибки приведен
на рис.3.3.
Рисунок 3.3 – Зависимостьизменения
интегрально-квадратичной ошибки
Рисунок 3.4 – Схема регулирования скорости в системе ТП-Д
Система регулирования скорости в схеме ТП-Д с нейроконтроллером
без компенсации противоЭДС, работающая от задатчика интенсивности ЗИ, приведена
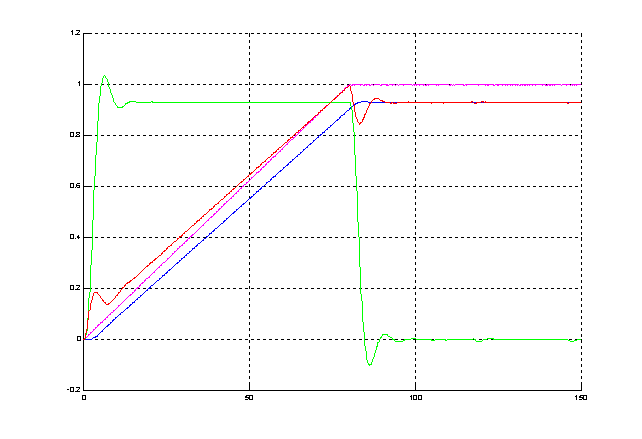
на рис.3.4.Переходные процессы, реализуемые этой схемой, показаны на рис.3.5.
Как видим, схема с нейроконтроллером реализует
такие же переходные процессы, как и схема с МР.
Рисунок 3.5 – Переходные процессы в схеме с нейроконтроллером
ЗАКЛЮЧЕНИЕ Применение нейросетей для управления электромеханической
системой наиболее целесообразно, когда неизвестна передаточная функция
объекта, либо в ней имеются сложные нелинейные зависимости.
Обратное распространение обладает преимуществом
прямого поиска, т. е. веса всегда корректируются в направлении, минимизирующем
функцию ошибки. Хотя время обучения и велико, оно существенно меньше, чем
при случайном поиске, когда находится глобальный минимум, но многие шаги
выполняются в неверном направлении, что отнимает много времени.
Несмотря на мощь, продемонстрированную методом
обратного распространения, при его применении возникает ряд трудностей,
часть из которых, однако, облегчается благодаря использованию нового алгоритма.
Сходимость. Доказательство сходимости дается на
языке дифференциальных уравнений в частных производных, что делает его
справедливым лишь в том случае, когда коррекция весов выполняется с помощью
бесконечно малых шагов. Так как это ведет к бесконечному времени сходимости,
то оно теряет силу в практических применениях. В действительности нет доказательства,
что обратное распространение будет сходиться при конечном размере шага.
Эксперименты показывают, что сети обычно обучаются, но время обучения велико
и непредсказуемо.
Локальные минимумы. В обратном распространении
для коррекции весов сети используется градиентный спуск, продвигающийся
к минимуму в соответствии с локальным наклоном поверхности ошибки. Он хорошо
работает в случае сильно изрезанных невыпуклых поверхностей, которые встречаются
в практических задачах. В одних случаях локальный минимум является приемлемым
решением, в других случаях он неприемлем.
Даже после того как сеть обучена, невозможно сказать,
найден ли с помощью обратного распространения глобальный минимум. Если
решение неудовлетворительно, приходится давать весам новые начальные случайные
значения и повторно обучать сеть без гарантии, что обучение закончится
на этой попытке или что глобальный минимум вообще будет когда либо найден.
Паралич. При некоторых условиях сеть может при
обучении попасть в такое состояние, когда модификация весов не ведет к
действительным изменениям сети. Такой «паралич сети» является серьезной
проблемой: один раз возникнув, он может увеличить время обучения на несколько
порядков.
Паралич возникает, когда значительная часть нейронов
получает веса, достаточно большие, чтобы дать большие значения NET.
Это приводит к тому, что величина OUT
приближается к своему предельному значению, а производная от сжимающей
функции приближается к нулю. Как мы видели, алгоритм обратного распространения
при вычислении величины изменения веса использует эту производную в формуле
в качестве коэффициента. Для пораженных параличом нейронов близость производной
к нулю приводит к тому, что изменение веса становится близким к нулю.
Если подобные условия возникают во многих нейронах
сети, то обучение может замедлиться до почти полной остановки.
Нет теории, способной предсказывать, будет ли сеть
парализована во время обучения или нет. Экспериментально установлено, что
малые размеры шага реже приводят к параличу, но шаг, малый для одной задачи,
может оказаться большим для другой. Цена же паралича может быть высокой.
При моделировании многие часы машинного времени могут уйти на то, чтобы
выйти из паралича.
Для избежания подобных недостатков представляется
возможным использование стохастических методов тренировки нейросетей, таких
как генетический алгоритм, которые позволяют тренировать нейроконтроллер,
не зная его выходной матрицы. В данном случае необходимо знать только желаемый
выход электромеханической системы.
Однако, несмотря на все выше перечисленные недостатки
алгоритма обратного распространения ошибки, его можно широко применять
для тренировки нейросетей при решении задач управления электромеханическими
системами, что и было продемонстрировано в данной работе.
![]() .(1.4)
.(1.4)
![]() .
.
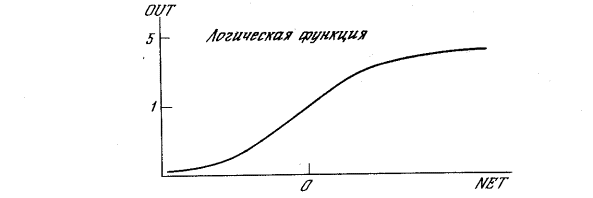
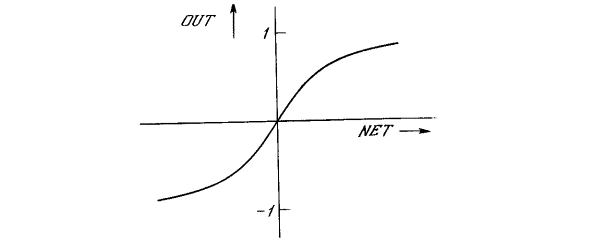
а – сигмоидальная логистическая; б – гиперболического тангенса
![]() .(2.1)
.(2.1)
![]() .(2.2)
.(2.2)
(e
– желаемый сигнал)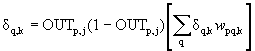 (2.7)
(2.7)
В СХЕМЕ ТП-Д С НЕЙРОКОНТРОЛЛЕРОМ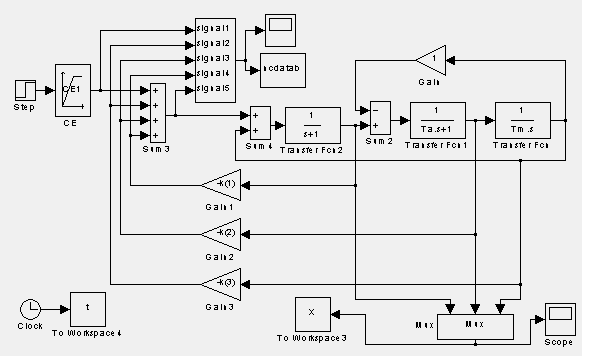
с задатчиком интенсивности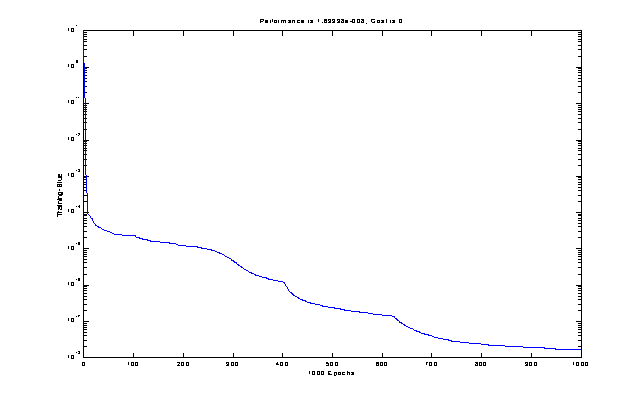
от количества эпох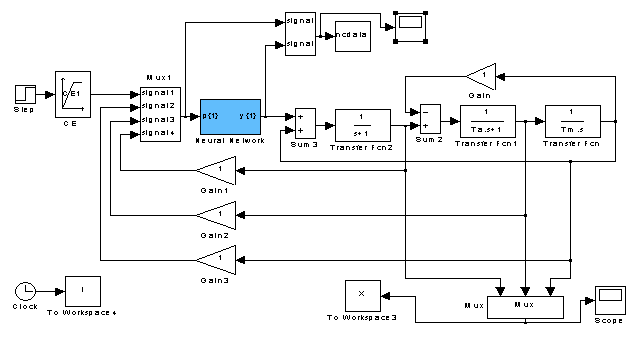
с нейроконтроллером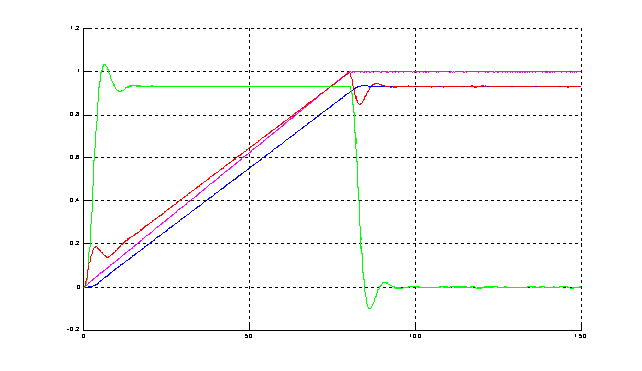
© Поляков В.А., 2000