На главную

---

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Васяева Татьяна Александровна Тема диссертации: "Разработка специализированной компьютерной системы на базе нейронных сетей для диагностики онкологических заболеваний кроветворных ткаеней." Специальность: 7.091505 "Компьютерные системы медицинской и технической диагностики." Автореферат магистерской выпускной работы Научный руководитель: д.т.н. профессор Скобцов Ю.А.

---

Актуальность.

Весь мир обеспокоен значительным ростом онкологических заболеваний. Украина не стала исключением. Oни занимают второе место в списке причин смертности (после сердечно-сосудистых). На сегодняшний день результатом лечения онкологических заболеваний кроветворных тканей отечественными методами лечения, является большое число рецидивов. Поэтому большинство наших онкологов относятся к этим болезням (в частности к лимфогранулематозу или Болезни Ходжкина) как в целом не излечимым заболеваниям, что не соответствует реальности. При достоверной диагностики, качественно и в срок проведенном стадировании, адекватной терапии семь из десяти первичных пациентов с Болезнью Ходжкина полностью излечиваются. По мировой статистике неудачи составляют 25-30% пациентов, большинство из которых по каким-либо причинам не прошли полный курс лечения.

Целью данной работы является достоверная диагностика и стадирование Болезни Ходжкина. Подбор схемы лечения и расчет необходимых доз препаратов, учитывая индивидуальные особенности пациента.

Принципы постановки диагноза.

Лимфогранулематоз - это опухолевое заболевание, при котором первично поражается лимфатическая система.

Опухолевым субстратом лимфогранулематоза является гигантская клетка Березовского-Штернберга.

Рис.1- Гистологический снимок лимфаузла. В центре гигантская клетка Березовского-Штернберга.

Диагноз лимфогранулематоза и стадирование производится один раз на протяжении всего курса лечения (и лечения рецидивов при их возникновении). Поэтому очень важно правильно поставить диагноз. Для установления максимально точного диагноза и стадии необходимо придерживаться единого плана обследования, который включает:

1. уточнение наличия у больного симптомов интоксикации (повышение температуры тела, профузный пот, похудание);
2. тщательный осмотр больного, включая пальпацию всех периферических лимфатических узлов (в том числе подключичных, локтевых и подколенных), пальпацию брюшной полости, в том числе печени, селезенки и области забрюшинных и подвздошных лимфатических узлов;
3. пункцию, а затем обязательную адекватную биопсию лимфатического узла. Для полноценной гистологической и иммунологической диагностики лимфатический узел необходимо представить в лабораторию целиком.
4. из лабораторных тестов обязательными являются: а) полный клинический анализ крови с определением числа лейкоцитов и лейкоцитарной формулы, уровня гемоглобина, тромбоцитов и СОЭ, б) биохимические пробы - исследование уровня щелочной фосфатазы, функции печени и почек, а также по возможности определение признаков биологической активности (содержание ?2-глобулина, фибриногена, гаптоглобина и церулоплазмина);
5. всем больным показано рентгенографическое исследование грудной клетки.
6. ультразвуковое исследование печени, селезенки, забрюшинных и внутрибрюшных лимфатических узлов, почек помогает исключить (или подтвердить) поражение этих органов.

Диагноз подтверждается только на основании гистологического заключения:

• Удаляется самый большой лимфатического узел;
• Делаются срезы по малой оси лимфатического узла;
• Производится фиксация в 10% растворе формалина;
• Выполняется обезвоживание в спиртах с постепенным увеличением концентрации;
• Уплотняется срез в парафине;
• Получают срезы с парафиновых блоков;
• Окрашивают;
• Заключение. (Диагноз ставится гистологом, при анализе образца с помощью микроскопа).

На основе гистологического анализа утверждена следующая классификация;

• лимфоидное преобладание;
• нодулярный (узловатый) склероз;
• смешанно-клеточный вариант;
• лимфоидное истощение.

Стадирование:

Стадия I	Вовлечение лимфатических узлов одного региона или одной лимфоидной структуры.
Стадия II	Вовлечение лимфатических узлов двух и более регионов по одну сторону диафрагмы.
Стадия III	Вовлечение лимфатических узлов регионов или структур по обе стороны диафрагмы.
Стадия IV	Вовлечение нелимфатического органа.

Каждая стадия может протекать с наличием А или Б симптомов.

А -	без симптомов интоксикации
В -	лихорадка, профузная потливость, потеря в весе.

При компьютерном анализе необходимо:

• распознать клетку Березовского-Штенберга по специфическим признакам и установить наличие клеток Ходжкина.
• Проанализировать состояние лимфатических узлов.
• Выявить симптомы интоксикации
• Проанализировать клинический анализ крови
• Установить диагноз, стадию, вариант
• Рекомендация схемы лечения и расчет доз.

Реализация поставленной задачи:

1. Прежде всего необходимо получить снимок гистологического образца. Для этого рекомендуется использовать световой микроскоп и цифровой фотоаппарат (например фирмы OLIMPYS), что позволит получить изображение в цифровой форме. Далее изображение анализируется. Учитываются следующие признаки: размер, форма, количество ядер, количество ядрышек.
2. На вход нейронной сети подается ряд признаков: анализ цифровой обработки, наличие симптомов интоксикации, показатели крови. На выходе получаем диагноз, определяем стадию и гистологический вариант.
3. По результатам диагноза и индивидуальным особенностям пациента подбирается схема лечения и рассчитываются дозы препаратов. Все данные хранятся в базе данных.

Основные положения нейронных сетей.

Как работает мозг.

Нервная система и мозг человека состоят из нейронов, соединенных между собой нервными волокнами. Нервные волокна способны передавать электрические импульсы между нейронами. Все процессы передачи раздражений от нашей кожи, ушей и глаз к мозгу, процессы мышления и управления действиями - все это реализовано в живом организме как передача электрических импульсов между нейронами.
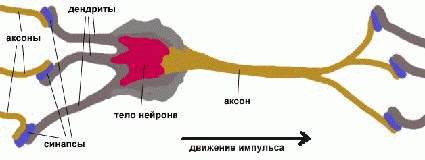
Рассмотрим строение биологического нейрона. Каждый нейрон имеет отростки нервных волокон двух типов - дендриты, по которым принимаются импульсы, и единственный аксон, по которому нейрон может передавать импульс. Аксон контактирует с дендритами других нейронов через специальные образования - синапсы, которые влияют на силу импульса.

Можно считать, что при прохождении синапса сила импульса меняется в определенное число раз, которое мы будем называть весом синапса. Импульсы, поступившие к нейрону одновременно по нескольким дендритам, суммируются. Если суммарный импульс превышает некоторый порог, нейрон возбуждается, формирует собственный импульс и передает его далее по аксону. Важно отметить, что веса синапсов могут изменяться со временем, а значит, меняется и поведение соответствующего нейрона.

Нетрудно построить математическую модель описанного процесса. На рисунке изображена модель нейрона с тремя входами (дендритами), причем синапсы этих дендритов имеют веса w₁, w₂, w₃. Пусть к синапсам поступают импульсы силы x₁, x₂, x₃ соответственно, тогда после прохождения синапсов и дендритов к нейрону поступают импульсы w₁x₁, w₂x₂, w_3>x₃. Нейрон преобразует полученный суммарный импульс x=w₁x₁+ w₂x₂+ w₃x₃ в соответствии с некоторой передаточной функцией f(x). Сила выходного импульса равна y=f(x)=f(w₁x₁+ w₂x₂+ w₃x₃).
Таким образом, нейрон полностью описывается своими весами w_k и передаточной функцией f(x). Получив набор чисел (вектор) x_k в качестве входов, нейрон выдает некоторое число y на выходе.

Что такое нейросеть

Как работает нейросеть

Искусственная нейронная сеть(ИНС, нейросеть) - это набор нейронов, соединенных между собой. Как правило, передаточные функции всех нейронов в сети фиксированы, а веса являются параметрами сети и могут изменяться. Некоторые входы нейронов помечены как внешние входы сети, а некоторые выходы - как внешние выходы сети. Подавая любые числа на входы сети, мы получаем какой-то набор чисел на выходах сети. Таким образом, работа нейросети состоит в преобразовании входного вектора в выходной вектор, причем это преобразование задается весами сети.
    Практически любую задачу можно свести к задаче, решаемой нейросетью. В этой таблице показано, каким образом следует сформулировать в терминах нейросети задачу распознавания рукописных букв.

  Поясним, зачем требуется выбирать выход с максимальным уровнем сигнала. Дело в том, что уровень выходного сигнала, как правило, может принимать любые значения из какого-то отрезка. Однако, в данной задаче нас интересует не аналоговый ответ, а всего лишь номер категории (номер буквы в алфавите). Поэтому используется следующий подход - каждой категории сопоставляется свой выход, а ответом сети считается та категория, на чьем выходе уровень сигнала максимален. В определенном смысле уровень сигнала на выходе "А" - это достоверность того, что на вход была подана рукописная буква "A".     Задачи, в которых нужно отнести входные данные к одной из известных категорий, называются задачами классификации. Изложенный подход - стандартный способ классификации с помощью нейронных сетей.

Как построить сеть

Теперь, когда стало ясно, что именно мы хотим построить, мы можем переходить к вопросу "как строить такую сеть". Этот вопрос решается в два этапа:

1. Выбор типа (архитектуры) сети.
2. Подбор весов (обучение) сети.

На первом этапе следует выбрать следующее:

• какие нейроны мы хотим использовать (число входов, передаточные функции);
• каким образом следует соединить их между собой;
• что взять в качестве входов и выходов сети.

Эта задача на первый взгляд кажется необозримой, но, к счастью, нам необязательно придумывать нейросеть "с нуля" - существует несколько десятков различных нейросетевых архитектур, причем эффективность многих из них доказана математически. Наиболее популярные и изученные архитектуры - это многослойный перцептрон, нейросеть с общей регрессией, сети Кохонена и другие. Про все эти архитектуры скоро можно будет прочитать в специальном разделе этого учебника.

На втором этапе нам следует "обучить" выбранную сеть, то есть подобрать такие значения ее весов, чтобы сеть работала нужным образом. Необученная сеть подобна ребенку - ее можно научить чему угодно. В используемых на практике нейросетях количество весов может составлять несколько десятков тысяч, поэтому обучение - действительно сложный процесс. Для многих архитектур разработаны специальные алгоритмы обучения, которые позволяют настроить веса сети определенным образом. Наиболее популярный из этих алгоритмов - метод обратного распространения ошибки (Error Back Propagation), используемый, например, для обучения перцептрона.

Обучение нейросети

  Обучить нейросеть - значит, сообщить ей, чего мы от нее добиваемся. Этот процесс очень похож на обучение ребенка алфавиту. Показав ребенку изображение буквы "А", мы спрашиваем его: "Какая это буква?" Если ответ неверен, мы сообщаем ребенку тот ответ, который мы хотели бы от него получить: "Это буква А". Ребенок запоминает этот пример вместе с верным ответом, то есть в его памяти происходят некоторые изменения в нужном направлении. Мы будем повторять процесс предъявления букв снова и снова до тех пор, когда все 33 буквы будут твердо запомнены. Такой процесс называют "обучение с учителем".
    При обучении сети мы действуем совершенно аналогично. У нас имеется некоторая база данных, содержащая примеры (набор рукописных изображений букв). Предъявляя изображение буквы "А" на вход сети, мы получаем от нее некоторый ответ, не обязательно верный. Нам известен и верный (желаемый) ответ - в данном случае нам хотелось бы, чтобы на выходе с меткой "А" уровень сигнала был максимален. Обычно в качестве желаемого выхода в задаче классификации берут набор (1, 0, 0, ...), где 1 стоит на выходе с меткой "А", а 0 - на всех остальных выходах. Вычисляя разность между желаемым ответом и реальным ответом сети, мы получаем 33 числа -вектор ошибки. Алгоритм обратного распространения ошибки - это набор формул, который позволяет по вектору ошибки вычислить требуемые поправки для весов сети. Одну и ту же букву (а также различные изображения одной и той же буквы) мы можем предъявлять сети много раз. В этом смысле обучение скорее напоминает повторение упражнений в спорте - тренировку.

Оказывается, что после многократного предъявления примеров веса сети стабилизируются, причем сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что "сеть выучила все примеры", " сеть обучена", или "сеть натренирована". В программных реализациях можно видеть, что в процессе обучения величина ошибки (сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда величина ошибки достигает нуля или приемлемого малого уровня, тренировку останавливают, а полученную сеть считают натренированной и готовой к применению на новых данных.
    Важно отметить, что вся информация, которую сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обучения сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу. Так, например, бессмысленно использовать сеть для предсказания финансового кризиса, если в обучающей выборке кризисов не представлено. Считается, что для полноценной тренировки требуется хотя бы несколько десятков (а лучше сотен) примеров.
Повторим еще раз, что обучение сети - сложный и наукоемкий процесс. Алгоритмы обучения имеют различные параметры и настройки, для управления которыми требуется понимание их влияния. Об этих тонкостях и о теоретических основах работы нейросетей скоро можно будет прочесть в специальном разделе этого учебника "Теория нейросетей".

Применение нейросети

Области применения нейросетей

Классификация

  Отметим, что задачи классификации (типа распознавания букв) очень плохо алгоритмизуются. Если в случае распознавания букв верный ответ очевиден для нас заранее, то в более сложных практических задачах обученная нейросеть выступает как эксперт, обладающий большим опытом и способный дать ответ на трудный вопрос.

Примером такой задачи служит медицинская диагностика, где сеть может учитывать большое количество числовых параметров (энцефалограмма, давление, вес и т.д.). Конечно, "мнение" сети в этом случае нельзя считать окончательным.

Классификация предприятий по степени их перспективности - это уже привычный способ использования нейросетей в практике западных компаний. При этом сеть также использует множество экономических показателей, сложным образом связанных между собой.

  Нейросетевой подход особенно эффективен в задачах экспертной оценки по той причине, что он сочетает в себе способность компьютера к обработке чисел и способность мозга к обобщению и распознаванию. Говорят, что у хорошего врача способность к распознаванию в своей области столь велика, что он может провести приблизительную диагностику уже по внешнему виду пациента. Можно согласиться также, что опытный трейдер чувствует направление движения рынка по виду графика. Однако в первом случае все факторы наглядны, то есть характеристики пациента мгновенно воспринимаются мозгом как "бледное лицо", "блеск в глазах" и т.д. Во втором же случае учитывается только один фактор, показанный на графике - курс за определенный период времени. Нейросеть позволяет обрабатывать огромное количество факторов (до нескольких тысяч), независимо от их наглядности - это универсальный "хороший врач", который может поставить свой диагноз в любой области.

Кластеризация и поиск зависимостей

Помимо задач классификации, нейросети широко используются для поиска зависимостей в данных и кластеризации.

Например, нейросеть на основе методики МГУА (метод группового учета аргументов) позволяет на основе обучающей выборки построить зависимость одного параметра от других в виде полинома. Такая сеть может не только мгновенно выучить таблицу умножения, но и найти сложные скрытые зависимости в данных (например, финансовых), которые не обнаруживаются стандартными статистическими методами.

Кластеризация - это разбиение набора примеров на несколько компактных областей (кластеров), причем число кластеров заранее неизвестно. Кластеризация позволяет представить неоднородные данные в более наглядном виде и использовать далее для исследования каждого кластера различные методы. Например, таким образом можно быстро выявить фальсифицированные страховые случаи или недобросовестные предприятия.

Прогнозирование

Задачи прогнозирования особенно важны для практики, в частности, для финансовых приложений, поэтому поясним способы применения нейросетей в этой области более подробно.

Рассмотрим практическую задачу, ответ в которой неочевиден - задачу прогнозирования курса акций на 1 день вперед.
    Пусть у нас имеется база данных, содержащая значения курса за последние 300 дней. Простейший вариант в данном случае - попытаться построить прогноз завтрашней цены на основе курсов за последние несколько дней. Понятно, что прогнозирующая сеть должна иметь всего один выход и столько входов, сколько предыдущих значений мы хотим использовать для прогноза - например, 4 последних значения. Составить обучающий пример очень просто - входными значениями будут курсы за 4 последовательных дня, а желаемым выходом - известный нам курс в следующий день за этими четырьмя.

  Если нейросеть совместима с какой-либо системой обработки электронных таблиц (например, Excel), то подготовка обучающей выборки состоит из следующих операций:

1. Скопировать столбец данных значений котировок в 4 соседних столбца.
2. Сдвинуть второй столбец на 1 ячейку вверх, третий столбец - на 2 ячейки вверх и т.д.

Смысл этой подготовки легко увидеть на рисунке - теперь каждая строка таблицы представляет собой обучающий пример, где первые 4 числа - входные значения сети, а пятое число - желаемое значение выхода. Исключение составляют последние 4 строки, где данных недостаточно - эти строки не учитываются при тренировке. Заметим, что в четвертой снизу строке заданы все 4 входных значения, но неизвестно значение выхода. Именно к этой строке мы применим обученную сеть и получим прогноз на следующий день.

Как видно из этого примера, объем обучающей выборки зависит от выбранного нами количества входов. Если сделать 299 входов, то такая сеть потенциально могла бы строить лучший прогноз, чем сеть с 4 входами, однако в этом случае мы имеем всего 1 обучающий пример, и обучение бессмысленно. При выборе числа входов следует учитывать это, выбирая разумный компромисс между глубиной предсказания (число входов) и качеством обучения (объем тренировочного набора).

Литература

• В.С. Медведев, В.Г. Потемкин Нейронные сети Matlab6.
• Владимир Дьяков, Владимир Круглов Математические пакеты расширения MATLAB Специальный справочник.
• Владимир Дьяконов, Ирина Абраменкова MATLAB Обработка сигналов и изображений.
• Руководство по гематологии. Том 1.
• Патолого-анатомическая диагностика опухолей человека.

Электронная библиотека	Cсылки и рез-ты поиска в Internet