ПРИМЕНЕНИЕ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕТОВ В НЕСТАЦИОНАРНОЙ ЗАДАЧЕ ТЕПЛОПРОВОДНОСТИ

Кравцов В.В. Шарай С.Я. Волкова О.Г.  Якубцов А.В.

Всегда для решения какой-то сложной задачи прибегают к некоторым упрощениям и допущениям. Какая-то реальная модель заменяется упрощённой, эквивалентной данной, которая позволяет не нарушить физический смысл рассматриваемых процессов в пределах каких-то погрешностей. Так в задаче нагрева тел неправильной формы успешно пользовались заменой их телами элементарной формы (цилиндр, параллелепипед…) Для таких тел была разработана методика расчёта при помощи критериев подобия и для облегчения расчётов составлены критериальные графики (Fo=(Bi,q)) Этот метод прост, но не учитывает зависимости физических свойств тела (l, с, r, а) от температуры. Естественно, что этот метод даёт очень приближённое решение.

С развитием вычислительной техники появилась возможность выполнения больших объёмов вычислений в за короткое время. Это дало толчок развитию математических методов, позволяющих более точно описать физические процессы в рассматриваемой задаче. Так в 60-х годах был разработан и эффективно использовался метод конечных разностей (МКР), который предполагает в себе разбиение тела сеткой и замены непрерывного функции конечными разностями. МКР – это большой шаг вперёд для решения задачи нагрева тел. Он уже позволил нестационарные задачи ( t=var ) с учётом изменения физических свойств тела в зависимости от температуры. Этот метод идеально подходит для тел элементарной формы и со значительной погрешностью может реализовать решение задачи нагрева для тела неправильной формы.

Подпись: а) б) Рисунок 1 – Разбиение тел неправильной формы сеткой конечных разностей (а) и сеткой конечных элементов (б) В 80-х годах появился и стал успешно использоваться метод конечных элементов (МКЭ). Он разрабатывался в США под руководством NASA и представлял собой стратегический объект развития государства. Этот метод более сложен, требующий значительных затрат на разработку приложений реализующих его и достаточно мощных вычислительных ресурсов. Сейчас МКЭ узко представлен в учебной литературе, только в отдельных изданиях, и не является легко доступным для специалистов отдельных областей наук.

Метод конечных элементов основан на идее аппроксимации непрерывной функции (в физической интерпретации - температуры, давления, перемещения и т.д.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых конечными элементами. Исследуемая геометрическая область разбивается на элементы таким образом, чтобы на каждом из них неизвестная функция аппроксимировалась пробной функцией (как правило, полиномом). Причем эти пробные функции должны удовлетворять граничным условиям непрерывности, совпадающим с граничными условиями, налагаемыми самой задачей. Выбор для каждого элемента аппроксимирующей функции будет определять соответствующий тип элемента.

В данной работе рассматривается вычислительный алгоритм метода конечных элементов в формулировке, основанной на процедуре минимизации функционала, соответствующего решаемой непрерывной задаче [1]. В результате выполнения указанной процедуры происходит замещение уравнения или системы уравнений в частных производных системой недифференциальных уравнений, имеющих в качестве коэффициентов аппроксимирующие функции, которые фактически являются значениями искомой функции в вершинах разбиения.

Метод конечных разностей (МКР) предоставил возможность заменить форму тела приближённой и произвести необходимые расчеты (рисунок 1 а)). Как шаг вперёд был разработан Метод конечных элементов (МКЭ), который позволяет разбить тело сеткой, практически повторяющей неправильную форму тела, другими словами, этот метод с большей степенью аппроксимирует форму тела, а значит и при решении задачи даёт меньшую погрешность. МКЭ предполагает работу с очень большими объёмами данных, что раньше затрудняло его применение, но теперь, мощность вычислительной техники позволяет его эффективно использовать для решения поставленных задач.

В качестве функции элемента приняли полином вида:

Некоторая область разбивается на конечные элементы (треугольники), каждый из которых описывается своим полиномом. В результате получаем аппроксимацию рассматриваемой области.

При разбиении области сеткой элементов следует придерживаться следующих правил:

1)     в местах с большим градиентом сетка должна быть меньше;

2)     Подпись: Рисунок 2 – Треугольный элемент элементы не должны иметь тупых углов (отображается на точности решения);

3)     необходимо выбрать абсолютную среднюю величину элемента, так как величина элемента влияет на точность решения задачи.

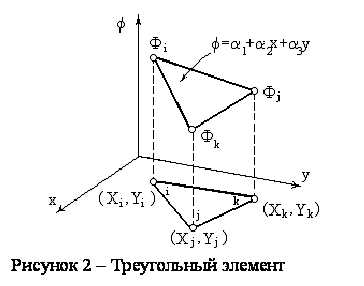
Рассмотрим один из элементов (рисунок 2). Это треугольник с прямолинейными сторонами и тремя узлами, в каждой вершине, причём нумерация узлов в каждом элементе проводится против часовой стрелки. Узловые значения некой величины  (в нашем случае это температура) обозначаются через  , а координаты трёх узлов – через (Х1;Y1), (X2;Y2), (X3;Y3). В узлах элемента выполняются условия:

 при ;

 при ;

 при .

Подстановка этих условий в формулу (1) приводит к системе уравнений:

æ ;

           í ;       (2)

è ;

Решая которую получаем :

 (3)

Здесь А – это площадь треугольника, связанная с определителем системы (2) соотношением :

Подставляя значения  в формулу (1) можно преобразовать выражение  к виду :

    (4)

Где

æ

 и í

è

æ

 и í

è

æ

 и í

è

Видно, что при определённых узловых значениях (с известными координатами узлов) можно определить значение полинома в любой точке, принадлежащей данному элементу. Функции  называют функциями формы.

Таким образом, совокупность конечных элементов (каждый из которых имеет строго определённое место в рассматриваемой области и свой полином) описывает температурное поле в этой области. В общей форме интерполяционный полином имеет вид :

æö

 íý       (5)

èø

(e) – означает, что уравнение относится к одному элементу. Суммируя уравнения для отдельных элементов, получаем :

     (6)

Где Е – число элементов. Это уравнение определяет область в целом.

В нашем случае рассматривается задача двумерного переноса тепла в сечении садки нагреваемого металла. Процесс нагрева описывается уравнением Фурье :

    (7)

qv – тепло, выделяемое внутренними источниками.

Пусть есть точное решение уравнения (7). При его подстановке в это уравнение получим тождество 0=0. Пусть  - приближённое решение уравнения, при подстановке которого получим не тождество, а некоторую невязку  отличную от нуля. Согласно методу Галёркина невязка будет минимальной при :

    (8)

Где  - некоторая система весовых функций.

    (9)

Так как область V разбита на конечные элементы, которые стыкуются между собой лишь на границах, то для обеспечения непрерывности функции  при переходе от элемента к элементу необходимо, чтобы вторая производная функции  существовала и была ограничена. При численном решении уравнения (7) это очень сильное условие. Учитывая это путём математических преобразований уравнение (9) примет вид :

       (10)

Это уравнение справедливо для i-того конечного элемента. Для всей области V будет справедлива сумма таких уравнений для всех элементов. Первые два интеграла – объёмные, а третий – поверхностный по площади S треугольника, в котором n – нормаль к поверхности S.

Согласно метода Галёркина невязка будет минимальна, если в качестве весовых функций выбрать функции формы , то есть

Выполним следующие преобразования согласно (5)

    (11)

Аналогично                            

Пользуясь:      и      преобразуем (10)

   (12)

Рассмотрим

Этот интеграл содержит в себе граничные условия :

1)                в случае ГУ 2-го рода он видоизменяется в : 

2)                в случае ГУ 3-го рода : 

где   - эквивалентный коэффициент теплоотдачи.

Здесь первый интеграл характеризует ГУ, а второй содержит в себе

То есть .  Тогда (12) примет вид :

   (13)

В сокращённом виде можно записать

Здесь [K] – матрица теплопроводности, которая учитывает физические свойства материала;

     [F] – вектор столбец нагрузки;

     {Ф} – искомый вектор столбец значений в узлах сетки.

Мы получили систему уравнений, которая описывает стационарную задачу распространения тепла, а для нестационарной решение уравнения будем искать в виде .

В результате в минимизируемый функционал добавляется ещё одно слагаемое, определяющее температурное поле (узловые значения) :

    (15)

Зная, что Wi=Ni и 

  (16)

Таким образом в уравнение (14) добавляется ещё одно слагаемое определяемое уравнением (16)

  (17)

Где [C] – матрица демпфирования, которая учитывает изменение температуры во времени.

Эффективность МКЭ можно улучшить повышая степень полинома элемента, увеличивая число узлов в элементе, или разбивать тело криволинейными элементами, что позволяет более точно аппроксимировать рассматриваемое тело.

При выполнении работы столкнулись с проблемой абсолютной величины конечного элемента, напрямую влияющего на точность получаемых результатов (пользуясь тем же сравнением с МКР). Установлено, что отклонения результатов напрямую зависят от абсолютной величины элемента.

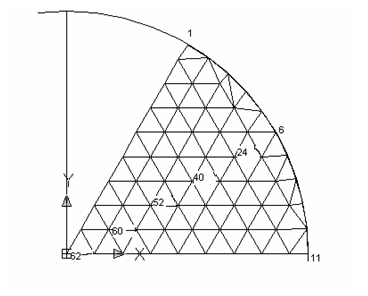Подпись: Таким образом, в результате проведенной работы была создана и опробована математическая модель нестационарной задачи и программа, реализующая расчёт нагрева тела методом конечных элементов. Программа тестировалась на примере нагрева бесконечно длинного цилиндра (сегмент цилиндра с сеткой разбиения изображён на рисунке 4), результаты расчетов проверялись в сравнении с результатами расчетов того же цилиндра методом конечных разностей неявной схемой (абсолютно устойчивая модель), для которого это одномерная задача. Сравнение результатов представлены на диаграмме (рисунок 5).

 

 

 

Список используемой литературы :

1. Зенкевич О. Метод конечных элементов в технике. -М.: Мир, 1975. - 318 с.

2. Сегерлинд Л. Применение метода конечных элементов. - М.:Мир, 1979. -392 с.