
Группа ПО-99а
Автореферат выпускной магистерской работы
Краткий обзор средств черчения в AutoCad
Знаменитый продукт компании Autodesk - AutoCAD является одной из самых популярных систем автоматизированного проектирования.
Система AutoCAD вычерчивает неоднородные рациональные В-сплайны (NURBS-кривые). Сплайны могут быть двумерными и трехмерными объектами, которые строятся на множестве точек.
Команды вычерчивания окружностей, эллипсов и их дуг включают:
В системе AutoCAD имеются команды генерации текста для нанесения однострочных текстов на чертежах (Text) и многострочных (Mtext).
Возможности языка AutoLisp
Встроенный в САПР AutoCAD интерпретатор языка AutoLISP (Автолисп) представляет собой конкретную реализацию функционального языка Лисп. Выбор столь экзотического языка в качестве встроенного для столь популярной САПР вызван тем, что список - оптимальный способ представления графической информации, а также легкостью реализации и небольшими размерами интерпретатора [7].
Где бы AutoCAD не запрашивал некий ввод (например, точку или масштабный фактор) для достижения необходимого значения могут быть использованы выражения AutoLISP этого типа или функции AutoLISP, возвращающие результат этого типа.
Начертательная геометрия: задачи и методы решения
1. Комплексный чертеж в прямоугольных проекциях
Начертательная геометрия - раздел геометрии, научные основы которого были разработаны французским математиком и физиком Г. Монжем для решения задач, связанных с определением размеров, форм и положения в пространстве линий, поверхностей, тел и их пересечений, при помощи построения их изображений на плоскости. Свойства геометрических фигур исследуются по их ортогональным проекциям, как правило, на три взаимно перпендикулярные плоскости, а геометрические построения в пространстве заменяются более доступными геометрическими построениями на соответствующих проекциях [9].
Для отображения вида сбоку (профильная проекция) проецирование осуществляется на третью плоскость, перпендикулярную П1 и П2 , обозначаемую П3.
2. Виды задач начертательной геометрии
Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических объектов. В связи с этим все многообразие задач может быть отнесено к двум группам:
В начертательной геометрии задачи решаются графически. Количество и характер геометрических построений при этом определяются не только сложностью задачи, но и в значительной степени зависит от того, с какими проекциями (удобными или неудобными) приходится иметь дело. При этом наиболее выгодным частным положением геометрического объекта следует считать:
При решении метрических задач, связанных с определением истинных размеров изображенных на эпюре фигур, могут встретиться значительные трудности, если заданные проекции не подвергнуть специальным преобразованиям [8].
3. Преобразование чертежа
Для упрощения решения метрических и позиционных задач инженерной графики применяются различные методы преобразования ортогональных проекций. После таких преобразований новые проекции позволяют решать задачу минимальными графическими средствами.
3.1 Замена плоскостей проекций
Метод замены плоскостей проекции основан на преобразовании проекций с помощью замены основных плоскостей проекций новыми, которые выбираются так, чтобы объект проецирования или его элементы изобразились на них в удобном для решения положении. При этом должно сохраниться ортогональное проецирование на взаимно перпендикулярные плоскости. Для решения той или иной задачи необходимо заменять одну, либо обе плоскости проекций.
3.2 Вращение вокруг линий уровня
Рассмотрим метод преобразования комплексного чертежа вращением вокруг линии уровня, который, в частности, может быть применим для решения метрической задачи нахождения натуральной величины треугольника.
Разработка алгоритмов автоматического решения задач начертательной геометрии
Существуют различные виды и методы решения задач начертательной геометрии. Создание универсального
алгоритма автоматического решения различных видов задач усложняется разнообразием подходов
к решению, вариантов конкретных методов, необходимостью учитывать частные случаи расположения
геометрических фигур в пространстве. Для решения же задач начертательной геометрии в системе AutoCAD существует множество инструментов,
с помощью которых можно решить поставленную задачу начертательной геометрии выбранным методом.
Ход построений, производимых пользователем, является, как правило, уникальным (выбор команд,
применяемая их последовательность, особенности построений выбранного метода).
Дальнейшее исследование и разработки будут направлены на реализацию автоматического решения некоторых
метрических задач методом замены плоскостей проекций.
Пример реализации решения задачи нахождения натуральной величины треугольника методом вращения
вокруг горизонтали
Обучение с использованием современных информационных технологий позволяет экономить силы и время при поиске
и передаче информации, при осуществлении инженерных расчетов, создании документов, рисунков, чертежей,
дает больше возможностей в повышении профессиональных качеств в целом.
Начертательная геометрия является одной из сложных дисциплин, изучаемых в техническом вузе.
Преподавание и изучение данной дисциплины традиционными методами является трудоемким и малоэффективным,
тем более что использование персональных компьютеров позволяет упростить этот процесс.
В мировой и отечественной практике широкое распространение получила система
автоматизированного проектирования AutoCAD.
Во многих вузах Украины базовым средством для освоения CAD является AutoCAD, его изучают даже школьники
в профильных учебных центрах [16]. В отдельных вузах СНГ при подготовке
инженерно-технических работников используют систему КОМПАС-ГРАФИК и другие [17].
Использование САПР позволяет оптимизировать работу инженера, но процесс ее выполнения
в среде САПР имеет свои особенности мышления [14]. Возникает необходимость подготовки
инженерно-технических работников, конструкторов-проектировщиков, умеющих работать в соответствии с
современными требованиями представления чертежей, выполнения конструкторской документации с помощью САПР.
Поэтому целесообразно использовать AutoCAD как наиболее распространенную САПР при изучении графических дисциплин
в вузах, начиная с основ начертательной геометрии.
Отметим, что в ДонНТУ для обучения начертательной геометрии применяются в основном
традиционные методы, но на кафедре ПМИ ДонНТУ лабораторные работы по начертательной
геометрии выполняются только в системе AutoCAD средствами точного построения. Курс "Инженерная графика" изучается для формирования умения читать графические документы и создавать чертежи и геометрические модели реальных или проектируемых объектов. В программе курса инженерной графики для направления подготовки "Компьютерные науки" предусматривается в основном изучение начертательной геометрии [1, 2].
На кафедре Прикладной математики и информатики ведется работа по подготовке учебно-методического материала,
представленного в виде электронных пособий и программных продуктов по изучению начертательной геометрии.
Для обучения студентов решению задач начертательной геометрии с использованием системы AutoCAD, а также для оценки их знаний в рамках решения той или иной задачи, появляется необходимость в создании специальной обучающей системы.
Была поставлена задача разработки системы, позволяющей автоматически решать задачи начертательной геометрии в среде AutoCADа. Такое автоматическое решение задач с разными условиями должно быть реализовано как для демонстрации решения, так и для проверки правильности решения при произвольных условиях (как "эталон для сравнения" [1]).
Такая обучающая система может использоваться как специальное средство дистанционного обучения начертательной геометрии.
В комплексе с электронным учебником по начертательной геометрии обучаемый сможет получить и теоретические основы,
и практические навыки. Основу образовательного процесса при дистанционном обучении составляет виртуальная форма обучения, т.е. самостоятельная работа обучаемого, который может учиться в удобном для себя месте, по индивидуальному расписанию [11].
Обратная же связь при этом осуществляется, прежде всего, в виде самоконтроля
обучаемых (при тестировании, при сравнении собственных построений и реализованных обучающей программой в режиме демонстрации), а также
посредством контроля преподавателя за процессом обучения (в том числе и с помощью функции тестирования).
Достоинством дистанционного обучения графическим дисциплинам есть также преобразование структуры операционного мышления, отношения к пространству чертежа,
получение необходимых навыков при решении задач, улучшение пространственного восприятия [12].
В рамках темы "Автоматическое решение задач начертательной геометрии" практическая часть магистерской работы будет заключаться в создании программного продукта, реализующего функции обучения и тестирования знаний средствами AutoCAD для целого класса задач одним или двумя методами решения задач начертательной геометрии.
Особенностью же автоматического решения задач является то, что система AutoCAD позволяет
реализовывать решение задач начертательной геометрии координатно-графическими методами.
Удобным инструментом решения задачи может служить язык AutoLISP, позволяющий осуществлять
операции с графическими объектами AutoCADа [1]. С помощью AutoLisp возможен доступ к базе
данных AutoCAD, к свойствам графических объектов.
Графический пользовательский интерфейс AutoCAD является понятным и удобным. В системе AutoCAD существуют различные возможности ввода команд: использование системного и контекстных меню, диалоговых окон, панелей инструментов и командной строки.
В AutoCAD можно задавать абсолютные и относительные прямоугольные и полярные координаты. Полярный и ортогональный режимы допускают перемещение графического курсора в различных направлениях по установленным пользователем углам. Шаговая привязка ограничивает перемещение курсора по узлам воображаемой сетки, интервал между которыми можно настраивать. Объектная привязка позволяет связывать точки построения новых элементов чертежа с существующими. Режим AutoSnap дает дополнительную возможность проверить и подтвердить отбор действий, выполняемых системой.
Шаблоны являются очень удобным средством стандартизации чертежей. В шаблоне содержится информация о таких параметрах, как размеры рабочего поля (лимиты чертежа), единицы измерения (десятичные или архитектурные) и др. Зачастую в шаблонах содержатся не только параметры настройки чертежа, но и стандартные фрагменты, например титульный блок - рамка и штамп с заготовкой основной надписи.
Базой, на которой строится создание чертежа, являются команды для построения геометрических примитивов.
Такие базовые команды группируются в меню Draw. К ним относятся команды вычерчивания линий:
- вычерчивание линий заданной толщины, состоящей из непрерывной последовательности отрезков прямых линий и дуг окружностей (Pline);
- вычерчивание гладких волнистых линий, линий обрыва или линий разграничения вида и разреза (Spline);
- вычерчивание луча, использующееся при выполнении дополнительных построений как база при вычерчивании контурных линий (Ray);
- вычерчивание прямой бесконечной линии, использующееся при выполнении дополнительных построений как база при вычерчивании контурных линий (Xline) [3].
Команды вычерчивания многоугольников включают:
- вычерчивание прямоугольников (Rectangle) [3].
- вычерчивание окружностей (Circle);
- вычерчивание эллипсов и эллиптических дуг (Ellipse).
Для нанесения штриховок различных образцов и параметров на чертежах используется специальные команды (Hatch, Вhatch).
Для создания из существующих объектов полилинии или области имеется команда Boundary.
Видоизменять чертеж, усложнять его, удалять ненужные или ошибочные элементы, редактировать тексты и образцы штриховок, пользователь может, используя команды меню Modify.
Свойства объектов редактируются с помощью команды Properties. Возможны разные операции над элементами чертежа: масштабирование, перенос, поворот, копирование, усечение, удлинение, сопряжение и пр.
AutoLisp является очень простым для изучения и очень мощным. Встроенный в AutoCad интерпретатор Лиспа позволяет вводить текст на языке AutoLisp в командной строке или загружать программы на AutoLisp из внешних файлов.
Зная AutoLisp, пользователь может вводить команды AutoLisp напрямую, получать к ним доступ, модифицировать и создавать объекты в графической базе данных, добавлять специфические возможности в AutoCad.
Некоторые стандартные команды AutoCad - в действительности "приложения" AutoLisp.
Visual Lisp обеспечивает 3 формата файлов для AutoLisp приложений: *.lsp
(Ascii файл текста программы на AutoLisp), *.fas (компилированная версия .lsp), *.vlx
(1 или несколько компилированных файлов *.lsp и DCL - dialog control language). Так как AutoCad может читать AutoLisp напрямую, то компиляция не нужна.
Сердцем интерпретатора Lisp является вычислитель. Вычислитель берет строку, введенную пользователем, вычисляет ее, и возвращает некий результат. Списки вычисляются в зависимости от первого элемента списка [6].
При вводе выражения AutoLISP в ответ на запрос "Command:" /команда:/, AutoLISP вычислит выражение и выведет результат на экран. Запрос AutoCAD "Command:" повторится. Если некорректное выражение набрано с клавиатуры или считано из файла, AutoLISP может выдать подсказку или сообщение об ошибке.
AutoLISP поддерживает несколько различных типов данных: списки, символы, строковые константы, действительные числа, целые числа, файловый дескриптор (описатель файлов), "имена" примитивов AutoCAD, наборы AutoCAD, встроенные функции. Диапазон целых 16-битовые чисел находится в пределах от -32768 до +32767. Действительные числа представлены как числа с плавающей запятой двойной точности. Строковые константы могут быть любой длины, память для них распределяется динамически. Однако существует максимальная длина для строковых констант, равная 100 символам.
При работе с координатами соблюдаются следующие соглашения:
Kаждая функция вызывается как список, первым элементом которого является имя функции (набранное в верхнем или нижнем регистре), а остальными - аргументы этой функции (если они есть) [6].
При построении чертежа могут использоваться различные функции языка AutoLisp. Рассмотрим некоторые из них.
Функция (command <аргумент>...) выполняет команды AutoCADа в AutoLISP и всегда возвращает nil. Аргументы представляют собой команды AutoCAD и их подкоманды; каждый аргумент вычисляется и посылается в AutoCAD, как ответ на соответствующий запрос. Kомандные имена и опции представляются как строковые константы, двумерные точки - как списки из двух действительных чисел, трехмерные точки - как списки из трех действительных чисел. Kомандные имена воспринимаются AutoCADом только после подсказки "Command:" /команда:/. Hапример:
(setq pt1 '(1.45 3.23))
(setq pt2 (getpoint "Enter a point: "))
(command "line" pt1 pt2)
(command "") [6].
Для работы со списками предусмотрено множество функций. Для создания списка используется функция setq, для доступа к элементам списка служат функции car, cdr и различные их комбинации (в виде cadr, caddr, cdar и пр.).
Арифметические функции суммы, вычитания, умножения, деления записываются в списковой форме вида: (<оператор> <число> <число>...). Наример, функция (+ <число> <число>...) возвращает сумму всех <чисел>.
Для организации ввода пользователем данных может использоваться функция (getint [<подсказка>]). Эта функция ожидает ввода пользователем целого числа и возвращает его. <Подсказка> - факультативная запись для высвечивания на экране в качестве подсказки.
Функция (getpoint [<точка>] [<подсказка>]) запрашивает от пользователя точку <точка>. Факультативный аргумент - базовая [<точка>] и [<подсказка>]. Можно ввести точку путем указания ее на экране или записав координаты в текущих единицах измерения. Обычно, getpoint возвращает двухмерную точку.
Функция (angle <точ1> <точ2>) возвращает угол (в радианах) между 2-мя лучами, направленными из 2-х мерной <точ1>. Первый - вдоль оси Х в сторону положительного направления, второй - в сторону двухмерной <точ2>, где двухмерная точка - список двух действительных чисел.
Функция (distance <точка1> <точка2>) возвращает расстояние между двухмерными точками <точка1> <точка2>.
Функция (inters <точка1> <точка2> <точка3> <точка4> []) проверяет два отрезка на пересечение и возвращает точку пересечения или nil, если они не пересекаются. <Точка1> и <точка2> крайние точки первого отрезка, <точка3> <точка4> - крайние точки второго отрезка. Если факультативный аргумент присутствует и является nil, то отрезки будут восприниматься бесконечной длины, и inters будет возвращать точку пересечения даже, если она находится за крайними точками одного или обоих отрезков. Если же аргумент отсутствует или не является nil, то точка пересечения должна находится на обоих отрезках, или inters вернет nil.
Имеются логические функции (and, or), перехода по условию (if), цикла (while) и прочие.
Для вывода данных на экран служат функции print, princ, prin1.
Чертежи должны быть по возможности наглядными, обратимыми, т.е. давать возможность точно воспроизводить форму и размеры предмета, обладать простотой построения. Черчение является интернациональным графическим языком, а грамматикой этого языка является начертательная геометрия [10].
Для отображения объектов на чертеже ставится задача определить проекции точек объекта на заданную плоскость. Существуют различные способы проецирования (центральное, косоугольное и прямоугольное (ортогональное)) и в зависимости от положения центров проецирования и плоскостей проекций могут быть получены различные проекционно-изобразительные системы. Наиболее распространенной системой является система прямоугольных (ортогональных) проекций, или метод Монжа.
Совокупность двух или более взаимосвязанных ортогональных проекций геометрической фигуры называется комплексным чертежом. Метод комплексного чертежа в прямоугольных проекциях называется методом Монжа [4].
Суть способа ортогонального проецирования заключается в том, что через каждую точку геометрической фигуры проводится проецирующая прямая, перпендикулярная плоскости проекций, и точка пересечения ее с этой плоскостью принимается за ортогональную проекцию точки.
В методе Монжа плоскости проекций П1 и П2 взаимно перпендикулярны, а центры проецирования удалены в бесконечность по направлениям, перпендикулярным к плоскостям проекций.
На рис. 1 плоскости проекций показаны сбоку по направлению их линии пересечения x12. Как видно из рисунка, неограниченные плоскости проекций П1 и П2 делят пространство на четыре четверти, показанные римскими цифрами. Для того, чтобы проекции точки получить на одной плоскости (плоскости чертежа), достаточно горизонтальную плоскость проекций П1 совместить с фронтальной плоскостью проекций П2 вращением вокруг линии их пересечения x12, или провести биссекторную плоскость К между П1 и П2, точку проецировать на эту плоскость в вертикальном направлении, а затем перепроецировать на фронтальную плоскость П1 (рис.2) [4].
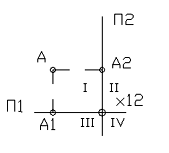
Рисунок 1 - Плоскости проекций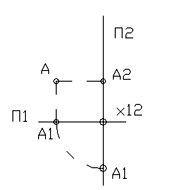
а)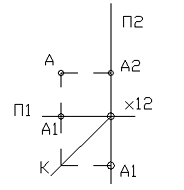
б)
Рисунок 2 - Получение проекций точки на одной плоскости чертежа:
а) совмещением П1 с П2 вращением вокруг линии их пересечения x12;
б) проецирование с помощью биссекторной плоскости К между П1 и П2
Введем некоторые понятия.
Изображение, получаемое при совмещении плоскостей проекций, называется "эпюр" [5].
Прямой уровня называется прямая, параллельная какой-либо одной плоскости проекций. Горизонталь - прямая, параллельная П1. Фронталь - прямая, параллельная П2. Профиаль - прямая, параллельная П3.
Проецирующие прямые - это такие прямые, которые перпендикулярны какой-либо одной плоскости проекций. Горизонтально-проецирующая прямая - прямая, перпендикулярная плоскости П1. Фронтально-проецирующая прямая - прямая, перпендикулярная плоскости П2. Профильно-проецирующая прямая - прямая, перпендикулярная плоскости П3.
Плоскости частного положения - это плоскости уровня и плоскости проецирующие. Плоскость уровня - это плоскость, параллельная одной из плоскостей проекций. Проецирующая плоскость - это плоскость, перпендикулярная какой-либо одной плоскости проекций. В зависимости от того, какой плоскости она перпендикулярна, ее называют фронтально- проецирующей, горизонтально- проецирующей и профильно-проецирующей.
К свойствам ортогонального проецирования относятся:
- положение, параллельное по отношению к плоскости проекций (при решении метрических задач).
Методы преобразования основываются, как правило, на двух принципах:
1) изменение взаимного положения объекта проецирования и плоскостей проекций;
2) изменение направления проецирования.
Первый принцип может быть реализован путем выбора новых плоскостей проекций при неподвижном положении объекта проецирования (метод замены плоскостей проекций) или перемещением объекта в новое положение относительно неподвижных плоскостей проекций (метод плоскопараллельного перемещения и метод вращения вокруг различных осей). Отмеченные методы используются в основном для решения метрических задач.
Метод преобразования проекций, основанный на изменении направления проецирования относительно неизменных плоскостей проекций (косоугольное вспомогательное проецирование), используется преимущественно для решения позиционных задач.
Существует еще ряд методов преобразования проекций, которые подробно рассматриваются в специальной литературе по начертательной геометрии [4].
Рассмотрим метод замены плоскостей проекций и метод вращения вокруг линии уровня.
Пусть задана система взаимно перпендикулярных плоскостей проекций П2/П1, точка А и ее проекции - в этой системе (А1; А2).
Пусть фронтальная плоскость проекции П2 заменена новой фронтальной плоскостью проекций П4 (новые фронтальные плоскости
проекций обычно обозначают четным цифровым индексом: П4; П6 и т. д., а горизонтальные - нечетным: П5; П7 и т.д. (плоскость П3 -
профильная плоскость проекций). Плоскость П4 проведена под произвольным углом к плоскости П2, но обязательно под прямым углом
к плоскости проекций П1. Горизонтальный след этой плоскости представляет собой новую ось проекций х14. Таким образом, от системы
плоскостей проекций П2/П1 мы перешли к системе П4/П1. Ортогонально спроецируем точку А на новую плоскость проекций П4 и получим
новую фронтальную проекцию А4 точки А. Расстояние от новой проекции точки до новой оси (А4А14) равно расстоянию от замененной
(старой) проекции точки до старой оси (А2А12), т. е. А4А14 = А2А12. Это и является инвариантом метода замены плоскостей проекции. В
новой системе плоскостей проекций П4/П1 получим пару проекций А1 и А4, которые также однозначно определяют положение точки А в
пространстве.
Для получения комплексного чертежа новой системы плоскостей проекций плоскость П4 вращением вокруг оси х14 совмещаем с плоскостью П1.
Тогда проекции А1 и А4 будут принадлежать линии связи, перпендикулярной к оси х14. Расстояние от А4 до оси х14 равно расстоянию
от А2 до оси х12 (рис. 3).
При замене горизонтальной плоскости проекций П1 на новую плоскость П5 получаем новую проекцию точки А5. И здесь расстояние от новой
проекции А5 до новой оси х25 (А5А25) равно расстоянию от заменяемой проекции А1 до старой оси х12 (А1А12): А1А12 = А5А25. Комплексный
чертеж новой системы получим, совместив плоскость П5 вращением вокруг оси х25 с плоскостью проекций П2. Проекции точки А2 и А5 также
располагаются на линии связи, перпендикулярной к оси х25 (рис. 4), а расстояние от А5 до оси х25 равно расстоянию от А1 до оси х12.
Замена двух плоскостей проекций выполняется последовательно: сначала заменяется одна плоскость (П2/П1 = П4/П1 или П2/П1 = П2/П5),
а затем в промежуточной системе вторая плоскость заданной системы (П4/П1= П4/П5 или П2/П5 = П4/П5). При второй замене (рис. 5)
плоскости проекций расстояние от новой проекции А5 точки А до новой оси х45 (А5А45) также равно расстоянию от заменяемой
проекции А1 до промежуточной (старой) оси х14 : А5А45 = А1А14 [4].
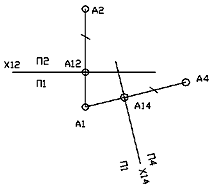
Рисунок 3 - Замена фронтальной плоскости проекций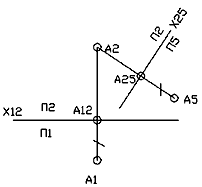
Рисунок 4 - Замена горизонтальной плоскости проекций
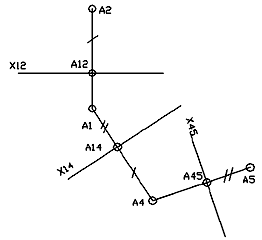
Рисунок 5 - Замена плоскостей проекций
Если вращать плоскость общего положения вокруг ее горизонтали или фронтали, то можно добиться, чтобы плоскость стала соответственно горизонтальной или фронтальной. При вращении вокруг горизонтали h (рис. 6) точка А описывает окружность, плоскость которой перпендикулярна к оси вращения h. Горизонтальная проекция траектории вращения точки изобразится прямой, проходящей через горизонтальную проекцию А1 точки, перпендикулярной к горизонтальной проекции горизонтали h1. Горизонтальная проекция центра вращения точки изобразится точкой О1. Отрезок А1О1 - это горизонтальная проекция радиуса вращения точки А. Точка А после поворота окажется лежащей в одной горизонтальной плоскости с горизонталью h, если радиус ее вращения на горизонтальной плоскости проекций изобразится в натуральную величину. Натуральная величина радиуса вращения АО определена способом прямоугольного треугольника как гипотенуза прямоугольного треугольника, один катет которого - отрезок А1О1, а второй равен разности координат концов z отрезка AO (zA - z0). Если от точки O1 на проекции траектории вращения точки А отложить в одну или другую сторону от проекции горизонтали натуральную величину радиуса вращения точки А, получим новую повернутую проекцию А11.
Если осью вращения будет фронталь f, то при вращении точка А описывает окружность, фронтальная проекция которой изобразится прямой, перпендикулярной к f2 (рис. 7). Определив натуральную величину радиуса вращения способом прямоугольного треугольника (O2A2 - величина одного катета, а разность координат (уА - у0) концов отрезка - величина второго), и отложив эту величину по одну и другую сторону f2 , получим повернутое положение А21 точки А [4].
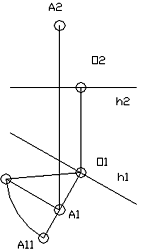
Рисунок 6 - Вращение вокруг горизонтали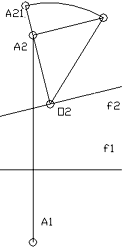
Рисунок 7 - Вращение вокруг фронтали
Поэтому задача исследования в рамках темы магистерской работы
сводится к поиску и классификации общих моментов в алгоритмах автоматического решения задач.
Следует отметить, что преподавателями и студентами многих вузов создаются электронные учебники [8, 10],
электронные задачники [15], а также обучающе-контролирующие программные комплексы по курсу начертательной геометрии.
В подобных разработках контроль знаний осуществляется в виде тестов "вопрос-ответ", теоретический материал
по курсу представлен статическими рисунками, а также с помощью мультимедиа средств.
Отметим, что описание функций модулей программного комплекса для постановки и решения задач по
начертательной геометрии [18], разработанного в МИФИ (Россия), в общем похоже на функции разрабатываемого
автором продукта, однако данный комплекс был выполнен на языке Turbo Pascal в операционной среде DOS,
что не соответствует современным требованиям к ПО.
Однако решения задачи в постановке, аналогичной теме данной магистерской работы,
при поиске в Интернет встречено не было. Преимуществом разрабатываемого продукта
является то, что обучение проходит в той же среде - в среде AutoCAD, в которой требуется от студентов
выполнение лабораторных работ. Контроль знаний предполагает проверку практического решения
конкретной задачи. При этом преподавателю нет необходимости самостоятельно проверять точность построений,
поскольку это сделает программа и выдаст результат.
При разработке алгоритмов и реализации системы обучения предусматриваются следующие
элементы:
При этом осуществляется ввод начала системы координат и исходных данных, проверка корректности ввода. Производится прорисовка осей координат и вывод соответствующих исходных данных в виде эпюра (фронтальная и горизонтальная проекция геометрических фигур).
Установлено, что графика, предъявленная в динамике, понимается и запоминается на
30-40% лучше, чем предъявленная в статике, и ЭВМ позволяет использовать это преимущество
динамической графики в интерактивном режиме. Этап материального действия должен постоянно сопровождаться ознакомлением
с действием [13].
В связи с этим пошаговая демонстрация геометрических построений
с комментариями облегчает понимание и запоминание.
Алгоритм демонстрации решения задачи может предусматривать запрос точки нового начала системы
координат, отличной от введенной при вводе исходных данных задачи. Это удобно, так как построения
не будут проводиться многократно на одном месте, кроме того, пользователь может параллельно отслеживать
построения, проводимые вызванной функцией, и анализировать собственные построения.
При разработке алгоритмов решения задач начертательной геометрии интересно также предусмотреть возможность
предварительной экспертной оценки задачи, подсказки пользователю элементов ее решения на отдельных
этапах.
Кроме того, планируется реализовать 3D-демонстрацию решения задач для
повышения понимания решения задач с помощью пространственного представления построений.
На данный момент реализован алгоритм решения задачи нахождения натуральной величины треугольника
методом вращения вокруг линии уровня.
Исходные данные задачи: А (18,30,5), В (10,10,12), С (15,15,20).
Демонстрация решения приведена на рис. 1 - 7. Анимация построения приведена на рис. 8.
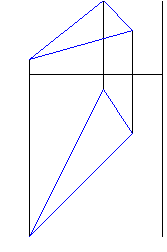
Рисунок 1 - Фронтальная и горизонтальная проекции треугольника |
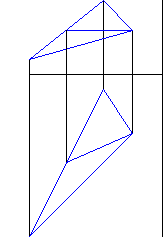
Рисунок 2 - Построение фронтальной и горизонтальной проекции горизонтали треугольника |
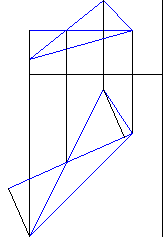 Рисунок 3 - Построение перпендикуляров к фронтальной и горизонтальной проекции горизонтали треугольника, опущенных из проекций вершин треугольника (кроме "средней") |
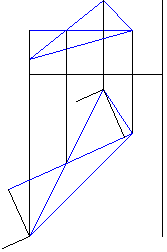 Рисунок 4 - Построение отрезков длинами перпендикуляров, опущенных из фронтальных проекций двух вершин треугольника (кроме "средней") к фронтальной проекции горизонтали, параллельно горизонтальной проекции горизонтали из соответствующих горизонтальных проекций точек " |
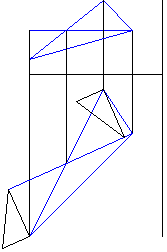 Рисунок 5 - Построение радиусов вращения вершин треугольника в натуральную величину |
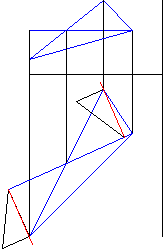 Рисунок 6 - Построение повернутых вокруг горизонтали проекций вершин треугольника |
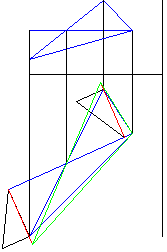 Рисунок 7 - Построение натуральной величины сторон треугольника |
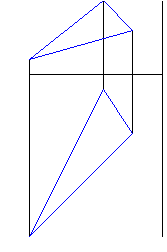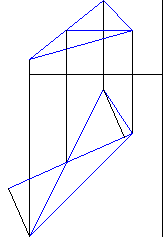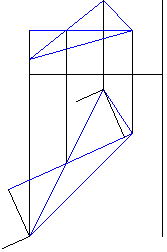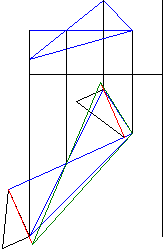 Рисунок 8 - Анимация построения натуральной величины треугольника (рис. 1-7) |
Литература
- Карабчевский В.В. Автоматическая генерация решения задач начертательной геометрии как средство формирования эталонов в подсистеме тестирования. // Научные труды Донецкого национального технического университета. Серия "Проблемы моделирования и автоматизации проектирования динамических систем" (МАП-2002). Выпуск 52: Донецк: ДонНТУ, 2002 г. - 248 с.
- Карабчевский В.В. Мультимедийный учебник по начертательной геометрии. // Образование и виртуальность-2002. Сборник научных трудов 6-й Международной ВИРТ-2003 конференции Украинской ассоциации дистанционного образования. Харьков-Ялта: УАДО, 2002 г.– с. 198 – 203.
- Федоренков А., Кимаев А. AutoCAD 2002: практический курс. - Москва: "ДЕСС КОМ", 2002 г. - 576 с., илл.
- Михайленко В.Е., Пономарев А.М. Инженерная графика: учебник для вузов.- 2-е изд., перераб. и доп. - К.: Вища шк. Голов. изд-во, 1985 г.- 295 с.
- Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. - М.: Наука, 1965 г., - 360 с., илл.
- Электронный учебник по языку AutoLisp
www.codenet.ru/progr/alisp - Троицкий Д.И. Программирование на AutoLisp: курс лекций. Тульский государственный университет, 1997-1999.
http://www.cad.dp.ua/kurs/ - Электронный учебник по начертательной геометрии.
http://www.propro.ru/bcad/graphbook/graphbook/book/soderzhanie.htm - Энциклопедия "Кругосвет". Начертательная геометрия.
http://krugosvet.ru - Лекции по начертательной геометрии.
http://yar-var.chat.ru/ingraph.htm - Кухаренко М.А., Олейник Т.А., Рыбалко Е.В., Савченко А.А. О некоторых аспектах развития информационно-образовательных технологий., Харьков.
users.kpi.kharkov.ua/lre/MicroCAD/mcad99/POLYTECH.htm - Сиротенко Н.Г., Филиппов В.В., Небратенко Ю.О. Дистанционное обучение: пути развития и совершенствования. Харьков, Украина.
users.kpi.kharkov.ua/lre/MicroCAD/mcad99/fil1.htm - Зиновченко А.Н. Психологические аспекты работы пользователя с обучающими программами.
users.kpi.kharkov.ua/lre/zin0209.html - Патраков А.Г. Сравнение методов выполнения конструкторской документации традиционным способом и с применением средств САПР.
Внедрение САПР в процесс обучения инженерной графике в вузах. (Московский государственный авиационный институт). Школа-семинар, Судак. 2001 г.
nit.itsoft.ru - Иванов А.В., Родионов В.В., Лысенко К.Н., Бочков А.М. Электронный задачник по начертательной геометрии. Пензенский технологический институт.
www.nocnit.ru/2st/materials/Ivanov.html - Мельник Александр. С AutoCAD по жизни. Компьютерное Обозрение, #12, 28 марта - 3 апреля 2001 г.
itc.ua - Харах М.М., Козлова И.А. Решение задач начертательной геометрии на основе информационных технологий. Астраханский государственный технический университет.
GraphiCon'2001, Нижний Новгород.
www.graphicon.ru/2001/pdf/Harah_Kozlova.pdf - Кисляков В.В., Осовец С.В. Программный комплекс для постановки и решения задач по начертательной геометрии.
ОТИ МИФИ. Электронная конференция ЭНИТ-2000, 17-19 мая, Ульяновск (Россия).
enit.ulsu.ru/d/003/