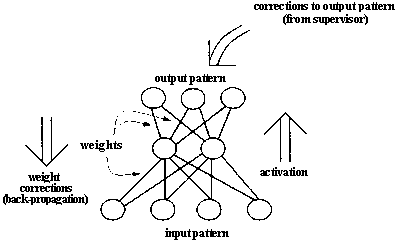
Neural networks are biologically motivated approaches to machine learning, inspired by ideas from neuroscience. Recently some efforts have been made to use genetic algorithms to evolve aspects of neural networks. Figure 2.16 A schematic diagram of a simple feedforward neural network and the back-propagation process by which weight values are adjusted.
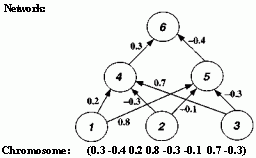
After activation has spread through a feedforward network, the resulting activation pattern on the output units encodes the network's "answer" to the input (e.g., a classification of the input pattern as the letter A). In most applications, the network learns a correct mapping between input and output patterns via a learning algorithm. Typically the weights are initially set to small random values. Then a set of training inputs is presented sequentially to the network. In the back-propagation learning procedure (Rumelhart, Hinton, and Williams 1986), after each input has propagated through the network and an output has been produced, a "teacher" compares the activation value at each output unit with the correct values, and the weights in the network are adjusted in order to reduce the difference between the network's output and the correct output. Each iteration of this procedure is called a "training cycle," and a complete pass of training cycles through the set of training inputs is called a "training epoch." (Typically many training epochs are needed for a network to learn to successfully classify a given set of training inputs.) This type of procedure is known as "supervised learning," since a teacher supervises the learning by providing correct output values to guide the learning process. In "unsupervised learning" there is no teacher, and the learning system must learn on its own using less detailed (and sometimes less reliable) environmental feedback on its performance. (For overviews of neural networks and their applications, see Rumelhart et al. 1986, McClelland et al. 1986, and Hertz, Krogh, and Palmer 1991.) Figure 2.17 Illustration of Montana and Davis's encoding of network weights into a list that serves as a chromosome for the GA. The units in the network are numbered for later reference. The real-valued numbers on the links are the weights.
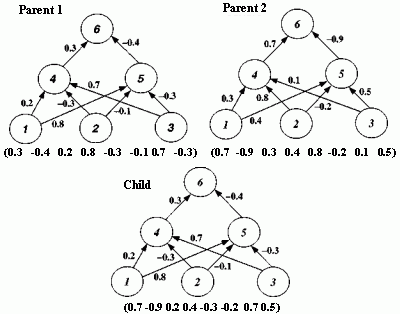
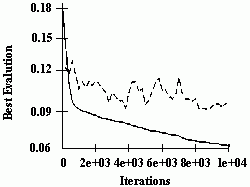
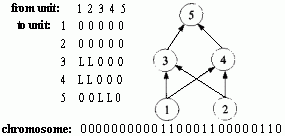
Figure 2.18 Illustration of Montana and Davis's mutation method. Here the weights on incoming links to unit 5 are mutated. Figure 2.19 Illustration of Montana and Davis's crossover method. The offspring is created as follows: for each non-input unit, a parent is chosen at random and the weights on the incoming links to that unit are copied from the chosen parent. In the child network shown here, the incoming links to unit 4 come from parent 1 and the incoming links to units 5 and 6 come from parent 2. Figure 2.20 Montana and Davis's results comparing the performance of the GA with back-propagation. The figure plots the best evaluation (lower is better) found by a given iteration. Solid line: genetic algorithm. Broken line: back-propagation. (Reprinted from Proceedings of the International Joint Conference on Artificial Intelligence; © 1989 Morgan Kaufmann Publishers, Inc. Reprinted by permission of the publisher.) Figure 2.21 An illustration of Miller, Todd, and Hegde's representation scheme. Each entry in the matrix represents the type of connection on the link between the "from unit" (column) and the "to unit" (row). The rows of the matrix are strung together to make the bit-string ' encoding of the network, given at the bottom, of the figure. The resulting network is shown at the right. (Adapted from Miller, Todd, and Hegde 1989.) Figure 2.22 Illustration of the use of Kitano's "graph generation grammar" to produce a network to solve the XOR problem, (a) Grammatical rules, (b) A connection matrix is produced from the grammar, (c) The resulting network. (Adapted from Kitano 1990.)
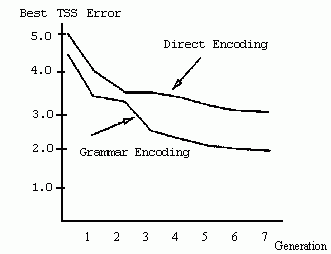
Figure 2.23 Illustration of a chromosome encoding a grammar. Figure 2.24 Results from Kitano's experiment comparing the direct and grammatical encoding methods. Total sum squared (TSS) error for the average best individual (over 20 runs) is plotted against generation. (Low TSS is desired.) (Reprinted from Kitano 1990 by permission of the publisher. © 1990 Complex Systems.) Figure 2.25 Illustration of the methd for encoding the kms in Chalmers's system.
In its simplest "feedforward" form (figure 2.16), a neural network is a collection of connected activa table units ("neurons") in which the connections are weighted, usually with real-valued weights. The network is presented with an activation pattern on its input units, such a set of numbers representing features of an image to be classified (e.g., the pixels in an image of a handwritten letter of the alphabet). Activation spreads in a forward direction from the input units through one or more layers of middle ("hidden") units to the output units over the weighted connections. Typically, the activation coming into a unit from other units is multiplied by the weights on the links over which it spreads, and then is added together with other incoming activation. The result is typically thresholded (i.e., the unit "turns on" if the resulting activation is above that unit's threshold). This process is meant to roughly mimic the way activation spreads through networks of neurons in the brain. In a feedforward network, activation spreads only in a forward direction, from the input layer through the hidden layers to the output layer. Many people have also experimented with "recurrent" networks, in which there are feedback connections as well as feedforward connections between layers.
There are many ways to apply GAs to neural networks. Some aspects that can be evolved are the weights in a fixed network, the network architecture (i.e., the number of units and their interconnections can change), and the learning rule used by the network. Here I will describe four different projects, each of which uses a genetic algorithm to evolve one of these aspects. (Two approaches to evolving network architecture will be described.) (For a collection of papers on various combinations of genetic algorithms and neural networks, see Whitley and Schaffer 1992.)
Evolving Weights in a Fixed Network
David Montana and Lawrence Davis (1989) took the first approach- evolving the weights in a fixed network. That is, Montana and Davis were using the GA instead of back-propagation as a way of finding a good set of weights for a fixed set of connections. Several problems associated with the back-propagation algorithm (e.g., the tendency to get stuck at local optima in weight space, or the unavailability of a "teacher" to supervise learning in some tasks) often make it desirable to find alternative weight-training schemes.
Montana and Davis were interested in using neural networks to classify underwater sonic "lofargrams" (similar to spectrograms) into two classes: "interesting" and "not interesting." The overall goal was to "detect and reason about interesting signals in the midst of the wide variety of acoustic noise and interference which exist in the ocean." The networks were to be trained from a database containing lofargrams and classifications made by experts as to whether or not a given lofargram is "interesting." Each network had four input units, representing four parameters used by an expert system that performed the same classification. Each network had one output unit and two layers of hidden units (the first with seven units and the second with ten units). The networks were fully connected feedforward networks-that is, each unit was connected to every unit in the next higher layer. In total there were 108 weighted connections between units. In addition, there were 18 weighted connections between the non-input units and a "threshold unit" whose outgoing links implemented the thresholding for each of the non-input units, for a total of 126 weights to evolve.
The GA was used as follows. Each chromosome was a list (or "vector") of 126 weights. Figure 2.17 shows (for a much smaller network) how the encoding was done: the weights were read off the network in a fixed order (from left to right and from top to bottom) and placed in a list. Notice that each "gene" in the chromosome is a real number rather than a bit. To calculate the fitness of a given chromosome, the weights in the chromosome were assigned to the links in the corresponding network, the network was run on the training set (here 236 examples from the database of lofargrams), and the sum of the squares of the errors (collected over all the training cycles) was returned. Here, an "error" was the difference between the desired output activation value and the actual output activation value. Low error meant high fitness.
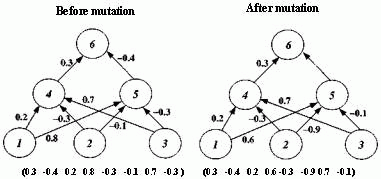
An initial population of 50 weight vectors was chosen randomly, with each weight being between -1.0 and +1.0. Montana and Davis tried a number of different genetic operators in various experiments. The mutation and crossover operators they used for their comparison of the GA with back-propagation are illustrated in figures 2.18 and 2.19. The mutation operator selects n non-input units and, for each incoming link to those units, adds a random value between -1.0 and +1.0 to the weight on the link. The crossover operator takes two parent weight vectors and, for each non-input unit in the offspring vector, selects one of the parents at random and copies the weights on the incoming links from that parent to the offspring. Notice that only one offspring is created.
The performance of a GA using these operators was compared with the performance of a back-propagation algorithm. The GA had a population of 50 weight vectors, and a rank-selection method was used. The GA was allowed to run for 200 generations (i.e., 10,000 network evaluations). The back-propagation algorithm was allowed to run for 5000 iterations, where one iteration is a complete epoch (a complete pass through the training data). Montana and Davis reasoned that two network evaluations under the GA are equivalent to one back-propagation iteration, since back-propagation on a given training example consists of two parts- the forward propagation of activation (and the calculation of errors at the output units) and the backward error propagation (and adjusting of the weights). The GA performs only the first part. Since the second part requires more computation, two GA evaluations takes less than half the computation of a single back-propagation iteration.
The results of the comparison are displayed in figure 2.20. Here one back-propagation iteration is plotted for every two GA evaluations. The x axis gives the number of iterations, and the у axis gives the best evaluation (lowest sum of squares of errors) found by that time. It can be seen that the GA significantly outperforms back-propagation on this task, obtaining better weight vectors more quickly.
This experiment shows that in some situations the GA is a better training method for networks than simple back-propagation. This does not mean that the GA will outperform back-propagation in all cases. It is also possible that enhancements of back-propagation might help it overcome some of the problems that prevented it from performing as well as the GA in this experiment. Schaffer, Whitley, and Eshelman (1992) point out that the GA has not been found to outperform the best weight-adjustment methods (e.g., "quickprop") on supervised learning tasks, but they predict that the GA will be most useful in finding weights in tasks where back-propagation and its relatives cannot be used, such as in unsuper-vised learning tasks, in which the error at each output unit is not available to the learning system, or in situations in which only sparse reinforcement is available. This is often the case for "neurocontrol" tasks, in which neural networks are used to control complicated systems such as robots navigating in unfamiliar environments.
Evolving Network Architectures
Montana and Davis's GA evolved the weights in a fixed network. As in most neural network applications, the architecture of the network-the number of units and their interconnections-is decided ahead of time by the programmer by guesswork, often aided by some heuristics (e.g., "more hidden units are required for more difficult problems") and by trial and error. Neural network researchers know all too well that the particular architecture chosen can determine the success or failure of the application, so they would like very much to be able to automatically optimize the procedure of designing an architecture for a particular application. Many believe that GAs are well suited for this task. There have been several efforts along these lines, most of which fall into one of two categories: direct encoding and grammatical encoding. Under direct encoding, a network architecture is directly encoded into a GA chromosome. Under grammatical encoding, the GA does not evolve network architectures; rather, it evolves grammars that can be used to develop network architectures.
Direct Encoding
The method of direct encoding is illustrated in work done by Geoffrey Miller, Peter Todd, and Shailesh Hegde (1989), who restricted their initial project to feedforward networks with a fixed number of units for which the GA was to evolve the connection topology. As is shown in figure 2.21, the connection topology was represented by an N x N matrix (5 x 5 in figure 2.21) in which each entry encodes the type of connection from the "from unit" to the "to unit." The entries in the connectivity matrix were either "0" (meaning no connection) or "L" (meaning a "learnable" connection-i.e., one for which the weight can be changed through learning). Figure 2.21 also shows how the connectivity matrix was transformed into a chromosome for the GA ("0" corresponds to 0 and "L" to 1) and how the bit string was decoded into a network. Connections that were specified to be learnable were initialized with small random weights. Since Miller, Todd, and Hegde restricted these networks to be feedforward, any connections to input units or feedback connections specified in the chromosome were ignored.
Miller, Todd, and Hegde used a simple fitness-proportionate selection method and mutation (bits in the string were flipped with some low probability). Their crossover operator randomly chose a row index and swapped the corresponding rows between the two parents to create two offspring. The intuition behind that operator was similar to that behind Montana and Davis's crossover operator-each row represented all the incoming connections to a single unit, and this set was thought to be a functional building block of the network. The fitness of a chromosome was calculated in the same way as in Montana and Davis's project: for a given problem, the network was trained on a training set for a certain number of epochs, using back-propagation to modify the weights. The fitness of the chromosome was the sum of the squares of the errors on the training set at the last epoch. Again, low error translated to high fitness.
Miller, Todd, and Hegde tried their GA on three tasks:
XOR: The single output unit should turn on (i.e., its activation should be above a set threshold) if the exclusive-or of the initial values (1 - on and 0 = off) of the two input units is 1.
Four Quadrant: The real-valued activations (between 0.0 and 1.0) of the two input units represent the coordinates of a point in a unit square. All inputs representing points in the lower left and upper right quadrants of the square should produce an activation of 0.0 on the single output unit, and all other points should produce an output activation of 1.0.
Encoder/Decoder (Pattern Copying): The output units (equal in number to the input units) should copy the initial pattern on the input units. This would be trivial, except that the number of hidden units is smaller than the number of input units, so some encoding and decoding must be done.
These are all relatively easy problems for multi-layer neural networks to learn to solve under back-propagation. The networks had different numbers of units for different tasks (ranging from 5 units for the XOR task to 20 units for the encoder/decoder task); the goal was to see if the GA could discover a good connection topology for each task. For each run the population size was 50, the crossover rate was 0.6, and the mutation rate was 0.005. In all three tasks, the GA was easily able to find networks that readily learned to map inputs to outputs over the training set with little error. However, the three tasks were too easy to be a rigorous test of this method-it remains to be seen if this method can scale up to more complex tasks that require much larger networks with many more interconnections. I chose the project of Miller, Todd, and Hegde to illustrate this approach because of its simplicity. For several examples of more sophisticated approaches to evolving network architectures using direct encoding, see Whitley and Schaffer 1992.
Grammatical Encoding
The method of grammatical encoding can be illustrated by the work of Hiroaki Kitano (1990), who points out that direct-encoding approachs become increasingly difficult to use as the size of the desired network increases. As the network's size grows, the size of the required chromosome increases quickly, which leads to problems both in performance (how high a fitness can be obtained) and in efficiency (how long it takes to obtain high fitness). In addition, since direct-encoding methods explicitly represent each connection in the network, repeated or nested structures cannot be represented efficiently, even though these are common for some problems.
The solution pursued by Kitano and others is to encode networks as grammars; the GA evolves the grammars, but the fitness is tested only after a "development" step in which a network develops from the grammar. That is, the "genotype" is a grammar, and the "phenotype" is a network derived from that grammar.
A grammar is a set of rules that can be applied to produce a set of structures (e.g., sentences in a natural language, programs in a computer language, neural network architectures). A simple example is the following grammar:
S ->aSb,
S->e
Here S is the start symbol and a nonterminal, a and b are terminals, and e is the empty-string terminal. (S ->o e means that S can be replaced by the empty string.) To construct a structure from this grammar, start with S, and replace it by one of the allowed replacements given by the right-hand sides (e.g., S -> aSb). Now take the resulting structure and replace any nonterminal (here S) by one of its allowed replacements (e.g., aSb -> aaSbb). Continue in this way until no nonterminals are left (e.g., aaSbb - >o aabb, using S -> e). It can easily be shown that the set of structures that can be produced by this grammar are exactly the strings a"b" consisting of the same number of as and bs with all the as on the left and all the bs on the right.
Kitano applied this general idea to the development of neural networks using a type of grammar called a "graph-generation grammar," a simple example of which is given in figure 2.22a. Here the right-hand side of each rule is a 2 x 2 matrix rather than a one-dimensional string. Capital letters are nonterminals, and lower-case letters are terminals. Each lower-case letter from a through p represents one of the 16 possible 2x2 arrays of ones and zeros. In contrast to the grammar for a"b" given above, each nonterminal in this particular grammar has exactly one right-hand side, so there is only one structure that can be formed from this grammar: the 8 x 8 matrix shown in figure 2.22b. This matrix can be interpreted as a connection matrix for a neural network: a 1 in row i and column i means that unit i is present in the network and a 1 in row i and column j, i Ф j, means that there is a connection from unit i to unit j . (In Kitano's experiments, connections to or from nonexistent units and recurrent connections were ignored.) The result is the network shown in figure 2.22c, which, with appropriate weights, computes the Boolean function XOR.
Kitano's goal was to have a GA evolve such grammars. Figure 2.23 illustrates a chromosome encoding the grammar given in figure 2.22a. The chromosome is divided up into separate rules, each of which consists of five loci. The first locus is the left-hand side of the rule; the second through fifth loci are the four symbols in the matrix on the right-hand side of the rule. The possible alleles at each locus are the symbols A-Z and a-p. The first locus of the chromosome is fixed to be the start symbol, S; at least one rule taking S into a 2 x 2 matrix is necessary to get started in building a network from a grammar. All other symbols are chosen at random. A network is built applying the grammar rules encoded in the chromosome for a predetermined number of iterations. (The rules that take a-p to the 162x2 matrices of zeros and ones are fixed and are not represented in the chromosome.) In the simple version used by Kitano, if a nonterminal (e.g., A) appears on the left-hand side in two or more different rules, only the first such rule is included in the grammar (Hiroaki Kitano, personal communication).
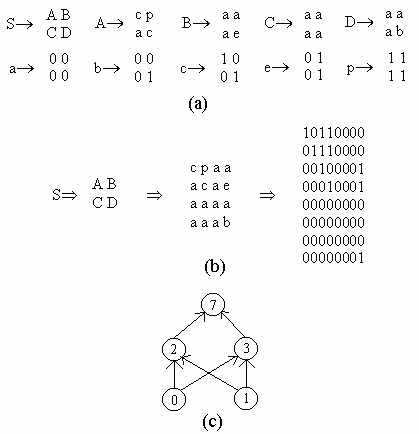

The fitness of a grammar was calculated by constructing a network from the grammar, using back-propagation with a set of training inputs to train the resulting network to perform a simple task, and then, after training, measuring the sum of the squares of the errors made by the network on either the training set or a separate test set. (This is similar to the fitness measure used by Montana and Davis and by Miller, Todd, and Hegde.) The GA used fitness-proportionate selection, multi-point crossover (crossover was performed at one or more points along the chromosome), and mutation. A mutation consisted of replacing one symbol in the chromosome with a randomly chosen symbol from the A-Z and a-p alphabets. Kitano used what he called "adaptive mutation": the probability of mutation of an offspring depended on the Hamming distance (number of mismatches) between the two parents. High distance resulted in low mutation, and vice versa. In this way, the GA tended to respond to loss of diversity in the population by selectively raising the mutation rate.
Kitano (1990) performed a series of experiments on evolving networks for simple "encoder/decoder" problems to compare the grammatical and direct encoding approaches. He found that, on these relatively simple problems, the performance of a GA using the grammatical encoding method consistently surpassed that of a GA using the direct encoding method, both in the correctness of the resulting neural networks and in the speed with which they were found by the GA. An example of Kitano's results is given in figure 2.24, which plots the error rate of the best network in the population (averaged over 20 runs) versus generation. In the grammatical encoding runs, the GA found networks with lower error rate, and found the best networks more quickly, than in the direct encoding runs. Kitano also discovered that the performance of the GA scaled much better with network size when grammatical encoding was used-performance decreased very quickly with network size when direct encoding was used, but stayed much more constant with grammatical encoding.
What accounts for the grammatical encoding method's apparent superiority? Kitano argues that the grammatical encoding method can easily create "regular," repeated patterns of connectivity, and that this is a result of the repeated patterns that naturally come from repeatedly applying grammatical rules. We would expect grammatical encoding approaches to perform well on problems requiring this kind of regularity. Grammatical encoding also has the advantage of requiring shorter chromosomes, since the GA works on the instructions for building the network (the grammar) rather than on the network structure itself. For complex networks, the latter could be huge and intractable for any search algorithm.
Although these attributes might lend an advantage in general to the grammatical encoding method, it is not clear that they accounted for the grammatical encoding method's superiority in the experiments reported by Kitano (1990). The encoder/decoder problem is one of the simplest problems for neural networks; moreover, it is interesting only if the number of hidden units is smaller than the number of input units. This was enforced in Kitano's experiments with direct encoding but not in his experiments with grammatical encoding. It is possible that the advantage of grammatical encoding in these experiments was simply due to the GA's finding network topologies that make the problem trivial; the comparison is thus unfair, since this route was not available to the particular direct encoding approach being compared.
Kitano's idea of evolving grammars is intriguing, and his informal arguments are plausible reasons to believe that the grammatical encoding method (or extensions of it) will work well on the kinds of problems on which complex neural networks could be needed. However, the particular experiments used to support the arguments are not convincing, since the problems may have been too simple. An extension of Kitano's initial work, in which the evolution of network architecture and the setting of weights are integrated, is reported in Kitano 1994. More ambitious approaches to grammatical encoding have been tried by Gruau (1992) and Belew (1993).
Evolving a Learning Rule
David Chalmers (1990) took the idea of applying genetic algorithms to neural networks in a different direction: he used GAs to evolve a good learning rule for neural networks. Chalmers limited his initial study to fully connected feedforward networks with input and output layers only, no hidden layers. In general a learning rule is used during the training procedure for modifying network weights in response to the network's performance on the training data. At each training cycle, one training pair is given to the network, which then produces an output. At this point the learning rule is invoked to modify weights. A learning rule for a single-layer, fully connected feedforward network might use the following local information for a given training cycle to modify the weight on the link from input unit i to output unit j:
aj: the activation of input unit i
oj : the activation of output unit j
tj. the training signal (i.e., correct activation, provided by a teacher) on output unit j
wij: the current weight on the link from i to j.
The change to make in weight to wij,del(wij) is a function of these values:
del(wij)=f(ai,oj,tj,wij)
The chromosomes in the GA population encoded such functions.
Chalmers made the assumption that the learning rule should be a linear function of these variables and all their pairwise products. That is, the general form of the learning rule was
del(wij) = k0(k1wij + k2ai + k3oj + k4tj + k5wijai + k6wijoj+k7wijtj+k8aioj+k9aiti+k10ojtj).
The km (1 <= m <= 10) are constant coefficients, and kg is a scale parameter that affects how much the weights can change on any one cycle, (ko is called the "learning rate.") Chalmers's assumption about the form of the learning rule came in part from the fact that a known good learning rule for such networks - the "Widrow-Hoff " or "delta" rule - has the form
del(wij)=n(tjoj-aioj)
(Rumelhart et al. 1986), where n is a constant representing the learning rate. One goal of Chalmers's work was to see if the GA could evolve a rule that performs as well as the delta rule.
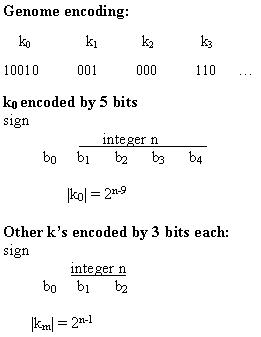
The task of the GA was to evolve values for the km's. The chromosome encoding for the set of km's is illustrated in figure 2.25. The scale parameter k0 is encoded as five bits, with the zeroth bit encoding the sign (1 encoding + and 0 encoding -) and the first through fourth bits encoding an integer n: k0 = 0 if n = 0; otherwise |k0| = 2n-9. Thus k0 can take on the values 0, ±1/256, ±1/128, . . ., ±32, ±64. The other coefficients km are encoded by three bits each, with the zeroth bit encoding the sign and the first and second bits encoding an integer n. For i = 1...10, km = 0 if n = 0; otherwise |km| = 2n-1.
It is known that single-layer networks can learn only those classes of input-output mappings that are "linearly separable" (Rumelhart et al. 1986). As an "environment" for the evolving learning rules, Chalmers used 30 different linearly separable mappings to be learned via the learning rules. The mappings always had a single output unit and between two and seven input units.
The fitness of each chromosome (learning rule) was determined as follows. A subset of 20 mappings was selected from the full set of 30 mappings. For each mapping, 12 training examples were selected. For each of these mappings, a network was created with the appropriate number of input units for the given mapping (each network had one output unit). The network's weights were initialized randomly. The network was run on the training set for some number of epochs (typically 10), using the learning rule specified by the chromosome. The performance of the learning rule on a given mapping was a function of the network's error on the training set, with low error meaning high performance. The overall fitness of the learning rule was a function of the average error of the 20 networks over the chosen subset of 20 mappings - low average error translated to high fitness. This fitness was then transformed to be a percentage, where a high percentage meant high fitness.
Using this fitness measure, the GA was run on a population of 40 learning rules, with two-point crossover and standard mutation. The crossover rate was 0.8 and the mutation rate was 0.01. Typically, over 1000 generations, the fitness of the best learning rales in the population rose from between 40% and 60% in the initial generation (indicating no significant learning ability) to between 80% and 98%, with a mean (over several runs) of about 92%. The fitness of the delta rule is around 98%, and on one out of a total of ten runs the GA discovered this rule. On three of the ten runs, the GA discovered slight variations of this rule with lower fitness.
These results show that, given a somewhat constrained representation, the GA was able to evolve a successful learning rule for simple single-layer networks. The extent to which this method can find learning rules for more complex networks (including networks with hidden units) remains an open question, but these results are a first step in that direction. Chalmers suggested that it is unlikely that evolutionary methods will discover learning methods that are more powerful than back-propagation, but he speculated that the GA might be a powerful method for discovering learning rules for unsupervised learning paradigms (e.g., reinforcement learning) or for new classes of network architectures (e.g., recurrent networks).
Chalmers also performed a study of the generality of the evolved learning rules. He tested each of the best evolved rules on the ten mappings that had not been used in the fitness calculation for that rule (the "test set"). The mean fitness of the best rules on the original mappings was 92%, and Chalmers found that the mean fitness of these rules on the test set was 91.9%. In short, the evolved rules were quite general.
Chalmers then looked at the question of how diverse the environment has to be to produce general rules. He repeated the original experiment, varying the number of mappings in each original environment between 1 and 20. A rule's evolutionary fitness is the fitness obtained by testing a rule on its original environment. A rule's test fitness is the fitness obtained by testing a rule on ten additional tasks not in the original environment. Chalmers then measured these two quantities as a function of the number of tasks in the original environment. The two curves are the mean evolutionary fitness and the mean test fitness for rules that were tested in an environment with the given number of tasks. This plot shows that while the evolutionary fitness stays roughly constant for different numbers of environmental tasks, the test fitness increases sharply with the number of tasks, leveling off somewhere between 10 and 20 tasks. The conclusion is that the evolution of a general learning rule requires a diverse environment of tasks. (In this case of simple single-layer networks, the necessary degree of diversity is fairly small.)
 To the library
To the library