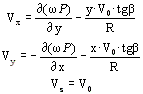
Суть винтовой экструзии заключается в продавливании призматической заготовки через
матрицу с винтовым каналом. Матрица состоит из 3 участков: заходной, винтовой,
калибрующий. Подвергая заготовку многократной экструзии (это возможно благодаря тому, что
конечная форма обрабатываемого металла такая же как и исходная) можно накапливать
деформацию, существенно изменяя структуру обрабатываемого металла. Это выполняется
с целью получения нанокристаллической структуры металла (размер структурного элемента
порядка 10-100 нм), которая обладает уникальными характеристиками по сравнению с металлом,
подвергнутому традиционной обработке.
На основании трех условий (граничных, несжимаемости металла, непроницаемости
инструмента) было предложено кинематически-возможное поле скоростей:
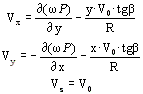
где w - так называемая функция формы канала, удовлетворяющая следующим
условиям: на стенках канала w=0,
внутри канала w>0, вне канала w<0.
P - произвольная функция (в даной работе Р(z)).
V0 - скорость прессования.
b - угол наклона винтовой линии к оси экструзии.
R - радиус канала матрицы.
В приведенном кинематически-возможном поле скоростей функция P(z) предназначена для учета
зон интенсивной деформации в начале и в конце очага деформации (винтового канала матрицы).
Для того, чтобы определить кинематически-возможное поле скоростей, решили воспользоваться
расчетно-экспериментальным методом. На основе этого подготовлен и проведен эксперимент: в
призматической заготовке просверлены 9 отверстий диаметром 1.2 мм, в них вставлена проволока 1 мм;
далее для того, чтобы закрепить метки произвели редуцирование заготовки с диаметром 29 до 27.5 мм.
Далее проводили непосредственно винтовую экструзию до того момента, когда образец заполнил
собой винтовую часть канала. После этого матрицу разобрали, извлекли образец, и с шагом 1 мм
перпендикулярно его продольной оси выполнили шлифование, каждое полученное сечение сканировалось.
Потом с помощью пакета Autocad определены координаты всех меток в каждом сечении и построены
кривые течения меток.
.gif)
Рисунок 1 – Скелет функции P(z); A, B, C1 и C2 – варьируемые параметры.
По координатам меток, полученным в результате эксперимента, и координатам, рассчитанным с помощью
вышеописанного поля, определяли суммарную невязку, представляющую собой сумму квадратов расстояний
теоретических меток от экспериментальных. Варьируемые параметры A, B, C1, C2 определялись путем
минимизации невязки с помощью пакета MathCad.
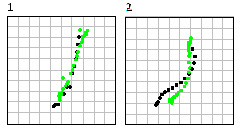
Расчетные и экспериментальные кривые движения меток 1 и 2
(зеленые экспериментальные, черные расчетные)
Соответствие вполне удовлетворительное. Некоторое расхождение экспериментально определенных и расчетных
координат точек, по-видимому, объясняется тем, что приведенное плоское кинематически-возможное поле
скоростей не позволяет учитывать происходящую при винтовой экструзии депланацию поперечных сечений.