Научно-практический журнал "Exponenta Pro. Математика в приложениях". Вышел 2/2004 номер журнала


Использование пакета Statistica 5.0 для статистической обработки опытных данных
С.В. Кабанов

Проведение регрессионного анализа при помощи модуля Multiple Regressions

В стартовом диалоговом окне этого модуля (рис. 27.) при помощи кнопки Variables указываются зависимая (dependent) и независимые (ая) (independent) переменные. В поле Input file указывается тип файла с данными:
Raw Date - данные в виде строчной таблицы;
Correlation Matrix - данные в виде корреляционной матрицы.
Рис.27 . Стартовое диалоговое окно модуля Multiple Regressions
В поле MD deletion указывается способ исключения из обработки недостающих данных:
casewise - игнорируется вся строка, в которой есть хотя бы одной пропущенное значение;
mean Substitution - взамен пропущенных данных подставляются средние значения переменных;
pairwise - попарное исключение данных с пропусками из тех переменных, корреляция которых вычисляется.
В поле Mode указывается тип регрессионной модели:
Standard - стандартная линейная модель вида:
Y = a1 + a2X1 + a3X2 + a3X3 + ... + anXn
Fixed non linear - фиксированная нелинейная, т.е. нелинейная модель, но которая может быть приведена к линейному виду путем преобразования переменных.
Рассмотрим проведение регрессионного анализа на примере. Имеются данные обмера и таксации 380 модельных деревьев различных древесных пород. В файле данных (рис. 30) 10 переменных:
1 PORODA Древесня порода (d- дуб, lp- липа, k- клен, o - осина)
2 A Возраст дерева, лет
3 D Таксационный диаметр ствола дерева в коре, см
4 H Высота дерева, м
5 VK Объем ствола в коре, куб.м
6 V Объем ствола без коры, куб.м
7 Q2 Второй коэффициент формы
8 L Длина кроны дерева, м
9 DKR Диаметр кроны дерева, м
10 F Старое видовое число

Рис.30. Вид окна с файлом данных
Найдем параметры регрессионного уравнения линейной связи объема ствола дуба в коре (переменная VK) от диаметра (D) и высоты (H) ствола. Вид уравнения: VK = a1 + a2D + a3H.
Выставим опции стартового окна регрессионного анализа (рис.29):
Variables: зависимая (dependent) переменная - VK; независимые (independent) - D,H (рис. 31); Input file - Raw Date (данные файла в виде строчной таблицы); MD deletion - pairwise; Mode - Standard.
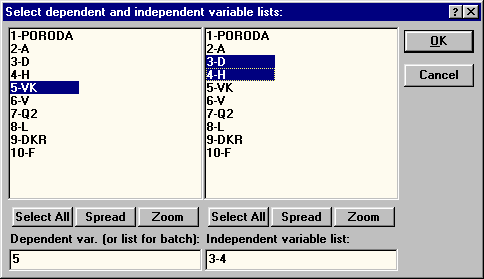Рис. 31. Выбор зависимой и независимых переменных
Так как в файле данных содержится информация о модельных деревьях разных пород, а уравнение регрессии мы хотим получить для дуба, нужно воспользоваться кнопкой Select cases диалогового окна Multiple Regressions чтобы установить условие включения случаев (строк файла данных) в статистическую обработку. В обработку должны включаться только те строки файла данных, для которых значение первой переменной V1 = 'd' (т.е. дуб) (рис. 32).
Рис. 32. Задание условия включения в обработку случаев со значением переменной V1 - дуб
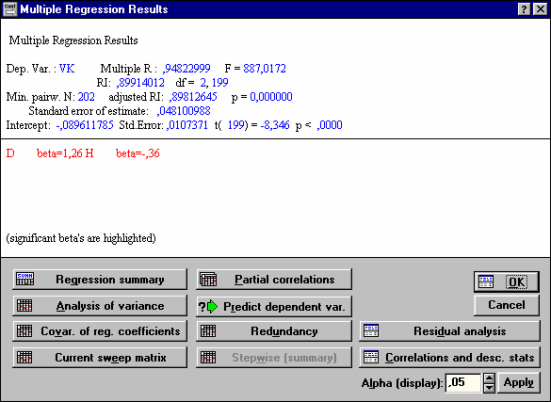После того, как все опции стартового диалогового окна регрессионного анализа выставлены, нажатие на кнопку ОК приведет к появлению окна Multi-ple Regressions Results (результаты регрессионного анализа) (рис. 33), с помощью которого можно просмотреть результаты анализа в деталях.
Рис. 33. Окно просмотра результатов регрессионного анализа
В верхней части окна приводятся наиболее важные параметры полученной регрессионной модели:
Multiple R - коэффициент множественной корреляции;
Характеризует тесноту линейной связи между зависимой и всеми независимыми переменными. Может принимать значения от 0 до 1.
R2 или RI - коэффициент детерминации;
Численно выражает долю вариации зависимой переменной, объясненную с помощью регрессионного уравнения. Чем больше R2, тем большую долю вариации объясняют переменные, включенные в модель.
adjusted R - скорректированный коэффициент множественной корреляции;
Этот коэффициент лишен недостатков коэффициента множественной корреляции. Включение новой переменной в регрессионное уравнение увеличивает RI не всегда, а только в том случае, когда частный F-критерий при проверке гипотезы о значимости включаемой переменной больше или равен 1. В противном случае включение новой переменной уменьшает значение RI и adjusted R2.
adjusted R2 или adjusted RI - скорректированный коэффициент детерминации;
Скорректированный R2 можно с большим успехом (по сравнению с R2) применять для выбора наилучшего подмножества независимых переменных в регрессионном уравнении.
F - F-критерий;
df - число степеней свободы для F-критерия;
p - вероятность нулевой гипотезы для F-критерия;
Standard error of estimate - стандартная ошибка оценки (уравнения);
Intercept - свободный член уравнения;
Std.Error - стандартная ошибка свободного члена уравнения;
t - t-критерий для свободного члена уравнения;
p - вероятность нулевой гипотезы для свободного члена уравнения.
Beta - 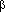-коэффициенты уравнения.
Это стандартизированные регрессионные коэффициенты, рассчитанные по стандартизированным значениям переменных. По их величине можно сравнить и оценить значимость зависимых переменных, так как -коэффициент показывает на сколько единиц стандартного отклонения изменится зависимая переменная при изменении на одно стандартное отклонение независимой переменной при условии постоянства остальных независимых переменных. Свободный член в таком уравнении равен 0.
При помощи кнопок диалогового окна Multiple Regressions Results (рис. 33) результаты регрессионного анализа можно просмотреть более детально.
Кнопка Regression summary - позволяет просмотреть основные результаты регрессионного анализа (рис. 34): BETA - коэффициенты уравнения; St. Err. of BETA - стандартные ошибки -коэффициентов; В - коэффициенты уравнения регрессии; St. Err. of B - стандартные ошибки коэффициентов уравнения регрессии; t (95) - t-критерии для коэффициентов уравнения регрессии; р-level - вероятность нулевой гипотезы для коэффициентов уравнения регрессии.
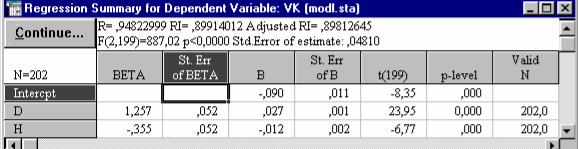Рис. 34. Основные результаты регрессионного анализа
Таким образом в результате проведенного регрессионного анализа получено следующее уравнение взаимосвязи между объемом ствола дуба в коре (VK) и диаметром (D) и высотой (H) ствола: VK = -0,090 + 0,027D - 0,012H. Все коэффициенты уравнения значимы на 5% уровне (p-level < 0,05). Это уравнение объясняет 89,9% (R2 = 0,899) вариации зависимой переменной. Ограничения модели: 2<=D>=31; 1,6<=H>=19,5.
Кнопка Analysis of variance - позволяет ознакомиться с результатами дисперсионного анализа уравнения регрессии (рис. 35). В строках таблицы дисперсионного анализа уравнения регрессии - источники вариации: Regress. - обусловленная регрессией, Residual- остаточная, Total - общая. В столбцах таблицы: Sums of Squares - сумма квадратов, df - число степеней свободы, Mean Squares - средний квадрат, F - значение F - критерия, p-level - вероятность нулевой гипотезы для F - критерия.
F - критерий полученного уравнения регрессии значим на 5% уровне. Вероятность нулевой гипотезы (p-level) значительно меньше 0,05, что говорит об общей значимости уравнения регрессии.
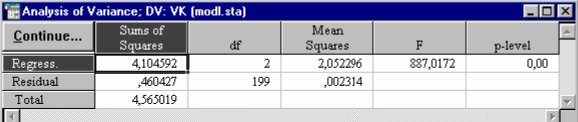Рис.35. Результаты дисперсионного анализа уравнения регрессии
Кнопка Partial correlations - позволяет просмотреть частные коэффициенты корреляции (Partial Cor.) между переменными (рис. 36). Частная корреляция - это корреляция между двумя переменными, когда одна или больше из оставшихся переменных удерживаются на постоянном уровне (т.е. имеют постоянное значение). Частные коэффициенты корреляции, как и парные, могут принимать значения от -1 до +1.
Рис. 36. Результаты расчета частных коэффициентов корреляции
Сильная взаимная коррелированность независимых переменных в нашем уравнении затрудняет анализ влияния отдельных факторов на зависимую переменную. Отрицательный знак коэффициента уравнения перед высотой (Н), отрицательный знак частного коэффициента корреляции VK c H противоречат реальному положению дел. Положительный знак парного коэффициента корреляции между высотой и объемом ствола говорит о прямой взаимосвязи между ними.
В идеальной регрессионной модели независимые переменные вообще не коррелируют друг с другом. Однако в моделях, разрабатываемых для природных объектов, сильная коррелированность переменных является довольно частым явлением. Это приводит к увеличению ошибок уравнения, уменьшению точность оценивания, снижается эффективность использования регрессионной модели. Поэтому выбор независимых переменных, включаемых в регрессионную модель, должен быть очень тщательным.
Кнопка Predict dependent var. - позволяет рассчитать по полученному регрессионному уравнению значение зависимой переменной по значениям независимых переменных. На рис. 37 приводится пример расчета объема ствола дуба в коре при величине диаметра ствола - 14 см и высоты - 11 м. Предсказанный (Predictd) объем составил 0,1614 куб.м.
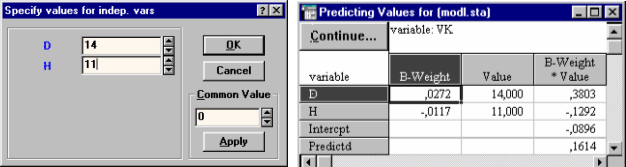Рис. 37. Окно задания значений независимых переменных и результаты расчета по регрессионному уравнению зависимой переменной
Кнопка Correlations and desc. stats позволяет просмотреть описательные статистики и корреляционную матрицу с парными коэффициентами корреляции переменных, участвующих в регрессионной модели (рис. 38).
Рис. 38. Диалоговое окно Review Descriptive Statistics
Кнопка Residual analysis запускает процедуру всестороннего анализа остатков регрессионного уравнения (рис. 39). Остатки - это разности между опытными и предсказанными значениями зависимой переменной в построен-ной регрессионной модели.
Рис.39 . Диалоговое окно Residual analysis (Анализ остатков)
Кнопка Redundancy предназначена для поиска выбросов. Выбросы - это остатки, которые значительно превосходят по абсолютной величине остальные. Выбросы показывают опытные данные, которые являются не типичными по отношению к остальным данным, и требует выяснения причин их возникновения. Выбросы должны исключаться из обработки, если они вызваны ошибками регистрации, измерения. Для выделения имеющихся в регрессионных остатках выбросов предложен ряд показателей:
Показатель Кука (Cook's Distance) - принимает только положительное значение и показывает расстояние между коэффициентами уравнения регрессии после исключения из обработки i-ой точки данных. Большое значение показателя Кука указывает на сильно влияющий случай.
Расстояние Махаланобиса (Mahalns. Distance) - показывает насколько каждый случай или точка в р-мерном пространстве независимых переменных отклоняется от центра статистической совокупности.
Внимательный анализ остатков позволяет оценить адекватность модели. Остатки должны быть нормально распределены, со средним значением равным нулю и постоянной, независимо от величин зависимой и независимой переменных, дисперсией. Модель должна быть адекватна на всех отрезках интервала изменения зависимой переменной.
Просмотр величин остатков и специальных критериев, их оценивающих, осуществляется при помощи кнопки Display residuals & pred. окна Residual analysis. Для нашего примера фрагмент окна с этими данные представлен на рис. 40.
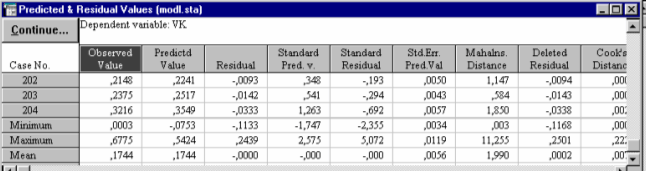Рис.40 . Окно со значениями остатков (Residuals), показателями Кука (Cook's Distance), расстояния Махаланобиса (Mahalns. Distance), опытными (Observed Value) и предстказанными по уравнению (Predictd Value) значениями зависимой переменной
Вполне достаточно бывает одного графического анализа остатков. О нормальности остатков можно судить по графику остатков на нормальной вероятностной бумаге. Чем ближе распределение к нормальному виду, тем лучше значения остатков ложатся на прямую линию. Он строится при помощи кнопки Normal plot of resids. окна Residual analysis (рис. 41).
Рис.41. График остатков на нормальной вероятностной бумаге
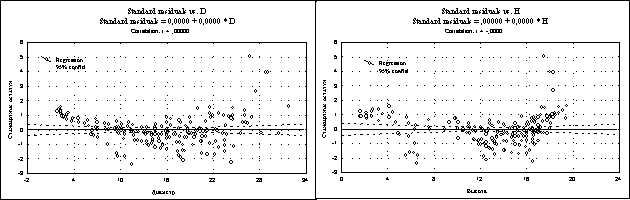Важно просмотреть графики зависимости остаток от каждой из независимых переменных. Их легко просмотреть при помощи кнопки Resids & indep. var. окна Residual analysis. Остатки должны быть нормально распределены, т.е. на графике они должны представлять приблизительно горизонтальную полосу одинаковой ширины на всем ее протяжении. Коэффициент корреляции (r) между регрессионными остатками и переменными должен равняться нулю.
Рис. 42. Зависимость остатков от независимых переменных: диаметра и высоты
В нашем случае на графиках остатков (рис. 42) хорошо просматривается нелинейный тренд, что вызывает сомнение в адекватности модели. Присутствие нелинейного тренда в регрессионных остатках говорит о необходимости пересмотра модели (преобразования или ввода новых переменных, перехода от линейной модели к нелинейной).
Рис. 43. Зависимость регрессионных остатков от предсказанных значений зависимой переменной
Для выявления нестабильности дисперсии ошибки уравнения при помощи кнопки Pred. & residuals окна Residual analysis можно создать график зависимости регрессионных остатков от предсказанного значения зависимой переменной. Рис. 43. позволяет заключить о непостоянстве дисперсии ошибки уравнения (с увеличением значений зависимой переменной дисперсия увеличивается). Это еще одной подтверждение неадекватности анализируемой модели.
Очень удобным визуальным способом оценки адекватности регрессионной модели является анализ графического изображения опытных и полученных по регрессионному уравнению значений зависимой переменной. Оно строится при помощи кнопки Pred. & observed окна Residual analysis.
Рис.44 . Линия регрессии, опытные и полученные по регрессионному уравнению значений зависимой переменной
Из рис. 44 хорошо видно, что линейный вид нашей модели плохо описывает взаимосвязь объема ствола дуба в коре от его диаметра и высоты (модель при малых и больших значениях отклика занижает величину зависимой переменной). Эта связь носит нелинейный характер.

Рассмотрим порядок нахождения коэффициентов уравнений регрессии нелинейного вида, но которые через преобразования переменных могут быть приведены к линейной модели. Найдем параметры регрессионного уравнения cвязи объема ствола дуба в коре (переменная VK) от диаметра (D) ствола. Вид уравнения: VK = a1 + a2D + a3D2.
Опцию Mode стартового окна регрессионного анализа (рис. 27) выставим в положение Fixed non linear. Если выбран фиксированный нелинейный тип регрессионной модели, то после нажатия на кнопку ОК в диалоговом окне Multiple Regressions (рис. 45), появляется окно Non-linear Components Regression (рис. .), в котором можно выбрать следующие типы преобразования переменных: X2, X3, X4, X5, 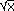(X0), lnX (X>0), lg10X (X>0), eX (40<X<-40), 10X (-18 to +18), 1/X (X0). Если потребуются какие либо иные преобразования переменных, то тогда в файле данных следует создать мнимые вичисляемые переменные и включить их в качестве зависимых переменных в регрессионную модель.
Рис. 45.Окно выбора типов преобразования переменных
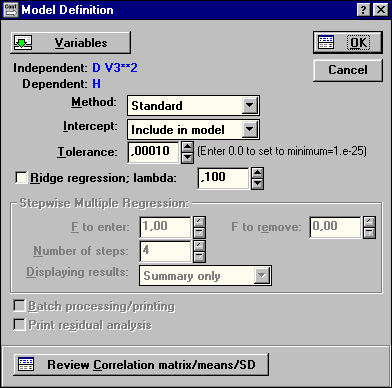После того, как тип преобразования переменных определен (в нашем примере это возведение в квадрат), необходимо уточнение зависимой и независимых переменных фиксированной нелинейной регрессионной модели. Оно производится на следующем шаге при помощи кнопки Variables диалогового окна Model Definition (Уточнение модели) (рис. 46).
Рис.46. Диалоговое окно Model Definition (Уточнение модели)
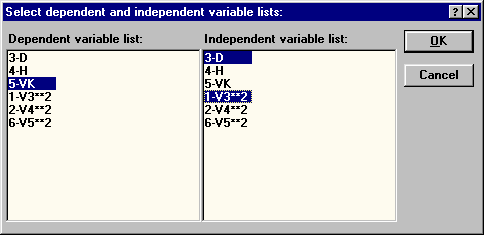Зависимой (dependent) переменной в нашем случае будет - VK; независимыми (independent) - D и D2 (рис. 47). Переменная D2 значится в списке переменных как V3**2, так как переменная D является третьей в списке переменных.
Рис. 47. Выбор переменных для расчета уравнения VK = a1 + a2D + a3D2
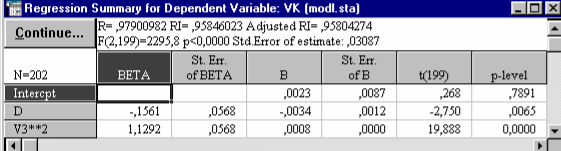Уравнение взаимосвязи между объемом ствола дуба в коре (VK) от его диаметром (D) оказалось сследующее: VK = 0,00023 - 0,0034D + 0,0008D2. Все коэффициенты уравнения (за исключением свободного члена) значимы на 5% уровне (p-level < 0,05). Это уравнение объясняет 95,8% (R2 = 0,958) вариации зависимой переменной (рис. 48).
Рис. 48. Результаты регрессионного анализа модели VK = a1 + a2D + a3
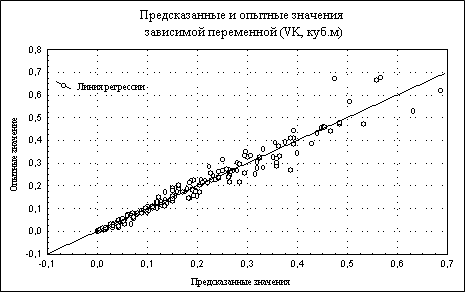Рис.49. Линия регрессии, опытные и полученные по регрессионному уравнению значений зависимой переменной
По всем стандартным параметрам второе уравнение регрессии значительно лучше первого. Это наглядно подтверждает и график на рис. 49.

Найдем параметры еще одного регрессионного уравнения. Вид уравнения: VK = a1Da2Ha3. Это степенное уравнение может быть приведено к линейному виду через логарифмирование: lnVK = lna1 + a2 lnD + a3 lnH.
При помощи кнопки Variables укажем зависимую - VK и независимые переменные - D,H. Опцию Mode стартового окна регрессионного анализа (рис. 27) выставим в положение Fixed non linear. В качестве типа преобразования переменных выберем натуральный логарифм (ln (Х)). В диалоговом окна Model Definition при помощи кнопки Variables уточним модель, переопределив зависимую и независимые переменные так, как это показано на рис. 50.
Рис. 50. Выбор переменных для расчета уравнения lnVK = lna1 + a2 lnD + a3 lnH
Рис. 51. Результаты регрессионного анализа модели lnVK = lna1 + a2 lnD + a3 lnH
Уравнение выглядит следующим образом: lnVK = -9,8789 + 1,8739lnD + 1,0346lnH или в степенном виде: VK = 0,00005 D1,8739 H1,0346. Все коэффициенты уравнения значимы на 5% уровне (p-level < 0,05). Это уравнение объясняет 99,6% (R2 = 0,996) вариации зависимой переменной. Ошибка уравнения 0,11405. Чтобы выразить ее в процентах, сравним абсолютную величину ошибки со средним значением зависимой переменной (lnVK): 0,11405/2,46166*100% = 4,6%.
Проверим адекватность полученной модели через анализ остатков. В целом он даст положительное заключение. В качестве иллюстрации приведем лишь несколько графиков (рис. 52, 53), подтверждающих такой вывод.
Рис. 52. Зависимость остатков степенного уравнения от независимых переменных: диаметра и высоты
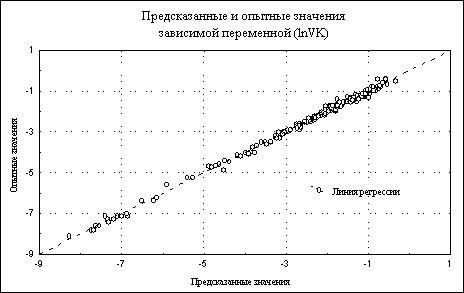Рис.53. Линия регрессии, опытные и полученные по степенному регрессионному уравнению значений зависимой переменной
Поиск наилучшей регрессионной модели представляет собой довольно громоздкий процесс. При помощи опции Method (рис. 27) пользователь может отказаться от стандартного проведения регрессионного анализа (Standard) и воспользоваться методами пошагового включения переменных в регрессионную модель (Forward stepwise) или пошагового исключения переменных (Backward stepwise) из регрессионной модели. Опция Displaying results позволяет просматривать или же только итоговые результаты регрессионного анализа (Summary only) или после каждого шага включения или исключения переменных (At each step). Если необходимо получить регрессионную модель без свободного члена уравнения, тогда в списке поля Intercept нужно выбрать - Set to zero.
Воспользуемся методом пошагового включения переменных для нахождения наилучшего регрессионного уравнения, описывающего объем ствола дуба в коре (VK). В качестве независимых переменных, которые потенциально могут быть включены в модель примем: диаметр ствола (D), квадрат диаметра (D2), высота ствола (Н), квадрат высоты ствола (Н2), произведение диаметра ствола на его высоту (DH), квадрат произведения диаметра ствола на его высоту ((DH)2).
В начале создадим новую переменную - DH. В файле данных она будет одиннадцатой по счету. Для расчета значений этой переменной вызовем окно с экспликацией этой переменной (рис. 54) и в поле Long name введем формулу, в соответствии с которой значения переменной должны быть рассчитаны, т.е "=V3*V4".
Рис.54. Окно экспликации 11-ой переменной
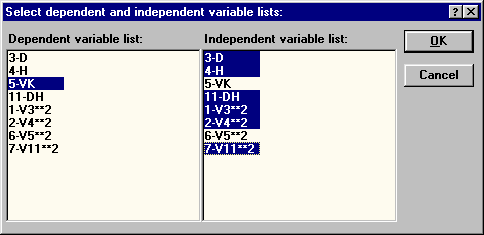Опцию Mode стартового окна регрессионного анализа (рис.27) выставим в положение Fixed non linear. Определим тип преобразования переменных - возведение в квадрат (рис. 45) и уточним зависимую и независимые переменные модели (рис. 55).
Рис.55. Уточнение зависимой и независимых переменных регрессионного анализа
Рис.56. Диалоговое окно Model Definition при использовании метода пошагового включения переменных в модель
Для пошаговых методов регрессионного анализа важно установить величину Tolerance (толерантность) и величины частного F- критерия для включения в модель (F to enter) и исключения из нее (F to remove). Установив величину толерантности мы создаем барьер для включения в модель переменных, толерантность которых меньше установленной. Если величина толерантности переменной мала, то переменная несет малую дополнительную информацию и включение ее в модель не целесообразно. Какая либо новая независимая переменная, включаемая в модель, может сильно влиять на зависимую переменную, но если она включается в модель после других переменных, она может уже мало влиять на переменную отклика (например, из-за сильной коррелированности с переменными, уже включенными в модель). По умолчанию в пакете Statistica переменная включается в модель, если частный F- критерий больше или равен 1. Численное значение F- критерия для включения никогда не выбирается меньшим, чем численное значение F- критерия для исключения.
Выставим опции окна Model Definition так, как показано на рис. 56. В результате процедуры пошагового включения переменных в регрессионную модель получено следующее уравнение (рис. ): VK = 0,0214 + 0,0009D2 -0,0104D + 0,0003(DH)2. Все коэффициенты уравнения значимы на 5% уровне (p-level < 0,05). Это уравнение объясняет 96,4% (R2=0,964) вариации зависимой переменной (рис. 57). Средняя ошибка уравнения составляет 0,02862 м3 .
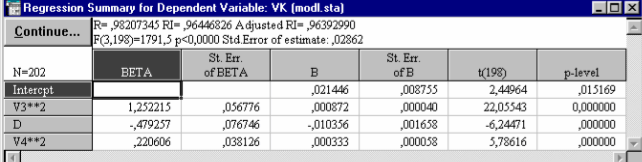Рис.57. Характеристика уравнения, полученного методом Forward stepwise
При поиске лучшей регрессионной модели следует руководствоваться следующими наиболее общими требованиями (Дрейпер, Смит, 1981):
  1. Регрессионная модель должна объяснять не менее 80% вариации зависимой переменной, т.е. R2 0.8.
  2. Стандартная ошибка оценки зависимой переменной по уравнению должна составлять не более 5% среднего значения зависимой переменной;
  3. Коэффициенты уравнения регрессии и его свободный член должны быть значимы на 5%-ом уровне.
  4. Остатки от регрессии должны быть без заметной автокорреляции (r<0,30), нормально распределены и без систематической составляющей.
Чем меньше сумма квадратов остатков, чем меньше стандартная ошибка оценки и чем больше R2, тем лучше уравнение регрессии.

Одним из недостатков классического регрессионного анализа, в основе которого лежит метода наименьших квадратов, является недостаточная устойчивость к изменениям входной информации. Сейчас довольно широко стали применяться альтернативные регрессионные модели, одной из которых является гребневая регрессия, которая отличается устойчивостью для случаев сильной коррелированности зависимых переменных друг с другом. В отличии от метода наименьших квадратов, дающего несмещенные оценки коэффициентов уравнения, в методе гребневой регрессии оценки смещенные, но при этом они имеют меньшую дисперсию. Поэтому такие оценки могут давать более точные и приемлемые для практического использования модели (Забелин, 1983).
Для расчета гребневой регрессии следует установить флажок в опции Ridge regression диалогового окна Model Definition.
При практическом использовании метода гребневой регрессии одним из основных вопросов является выбор параметра (lambda). Существует несколько численных методов расчета параметра, но чаще используют простой эмпирический подход: выбирают такой параметр , при котором коэффициенты стабилизируются и при дальнейшем увеличении параметра изменяются мало. Значение принятого параметра является мерой смещения оценок от истинного значения, поэтому стараются не придавать слишком больших значений. Обычно выбирают меньше 0,5, а шаг при подборе выбирают небольшим, например, 0,02 (Уланова, Забелин, 1990). При =0 уравнение имеет коэффициенты классического метода наименьших квадратов.