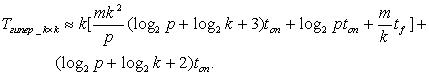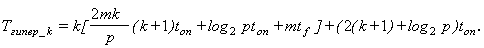Данная статья предназначена для публикации в сборнике трудов магистрантов
АНАЛИЗ ПАРАЛЛЕЛЬНЫХ ЧИСЛЕННЫХ МЕТОДОВ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДУ И ИХ ОТОБРАЖЕНИЕ НА ПАРАЛЛЕЛЬНЫЕ СТРУКТУРЫ
Панченко О.Г.
Донецкий национальный технический университет
E-mail po@donapex.net
Abstract
Panchenko O. Analysis of the parallel numerical methods
for decision Cauchy problem for ODE and their reflection
on parallel structure.
In represented article the analysis
of parallel algorithms for the decision of ordinary differential
equations on computing structures with SIMD by architecture
is considered. Reflection of extra-exact multistep block algorithms
on parallel calculable structures SIMD types with lattice and
gipercub topology is showed. Parallelizm estimations are considered:
acceleration and effectiveness for offered decision reflection methods.
Введение
С развитием техники перед учеными ставятся все более сложные
цели, достижение которых требует оригинального мышления
и повышенной внимательности. Постоянные исследования
в области разработки и создания высокопроизводительных
вычислительных средств позволяют решать фундаментальные
и прикладные задачи. Производительности современных ЭВМ
недостаточно для обеспечения нужного решения многих задач.
Один из наиболее эффективных способов повышения
производительности заключается в распараллеливании
вычислений в многопроцессорных и параллельных структурах,
создание новых методов и алгоритмов, ориентированных на
эффективное использование в многопроцессорных системах,
а также модернизация существующих методов. [6] Многие
численные методы не подходят для распараллеливания и их
приходится перестраивать либо совсем от них отказываться.
Некоторые же параллельные методы обладают численной
неустойчивостью или имеют очень сложную структуру, которая
приводит к потере эффективности.
К методам, которые не обладают указанными недостатками,
можно отнести блочные [1]. Идея этих методов состоит в том,
что, имея k точек блока, новые k значений можно вычислить
одновременно. Данная особенность методов согласуется с
архитектурой параллельных ВС и позволяет вычислять
коэффициенты разностных формул не в процессе интегрирования,
а на этапе разработки метода, что значительно увеличивает
эффективность счета. Данная работа опирается на исследования,
результаты которых ранее опубликованы авторами в [2,3,4,5] и
посвящена анализу параллельных методов решения задачи Коши
для ОДУ и СОДУ и их отображению на параллельные структуры.
1. Алгоритмы параллельного решения задачи Коши для ОДУ
Рассмотрим решение задачи Коши
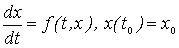
|
(1)
|
k точечным блочным разностным методом.
Множество M точек равномерной сетки tm,
m=1,2,…,M и tM=T разобьем на N блоков, содержащих
по k точек, при этом kN>=M. В каждом блоке введем
номер точки i =0,1,…,k и обозначим через tn,i точку
n-го блока с номером i. Точку tn,0 назовем начальной
точкой блока n, а tn,k – конечной точкой блока.
Очевидно, что имеет место равенство tn,k = tn+1,0.
Если для расчета значений в новом блоке используется только
последняя точка предшествующего – будем говорить об одношаговых,
а если все точки предшествующего блока – многошаговых блочных
методах.
В общем случае уравнения многошаговых разностных методов
для блока из k точек с учетом введенных обозначений можно
записать в виде: [2]
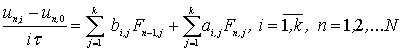
|
(2)
|
где
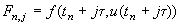 . .
|
Для одношаговых разностных методов уравнения могут
быть представлены как
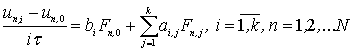
|
(3)
|
Выражение для погрешности аппроксимации рассматриваемого
метода (2) на решении уравнения (1) можно записать следующим
образом:
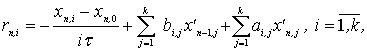
|
(4)
|
где
Разлагая xn,i, x'n,j и x'n-1,j в ряды
Тейлора в окрестности точки tn, и учитывая,
что конечная точка предыдущего блока совпадает с
начальной точкой следующего блока, будем иметь: [4]
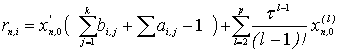 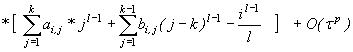
|
(5)
|
Можно видеть, что погрешность аппроксимации имеет порядок p,
если выполнены условия
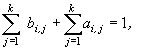 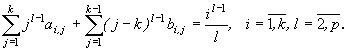
|
(6)
|
Чтобы из системы (6) определить все коэффициенты нужно,
чтобы p=2k. Отсюда следует, что наивысший порядок
аппроксимации многошагового k-точечного блочного
метода равен 2k. Его погрешность в соответствии с (5)
определяется формулой
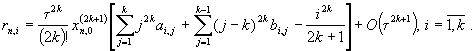
|
(7)
|
Для одношаговых блочных методов аппроксимацию
порядка p обеспечивают следующие условия [3]
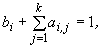 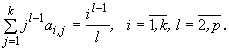
|
(8)
|
Аналогично для определения неизвестных нужно потребовать,
чтобы p=k+1. Отсюда следует, что наивысший порядок
аппроксимации одношагового k-точечного блочного метода
равен k+1. Его погрешность имеет вид:
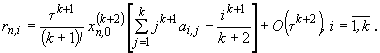
|
(9)
|
Для вычисления приближенных значений решения задачи Коши (1)
необходимо решить нелинейную систему уравнений (2).
Используем для этого следующий итерационный процесс:
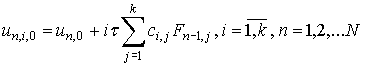
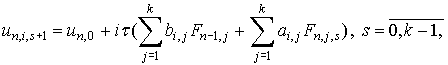
|
(10)
|
который позволяет проводить вычисления параллельно
для каждого узла блока.
После выполнения k шагов вычислений по формулам (10)
локальная ошибка в узлах блока будет иметь порядок 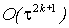 .
Для одношаговых блочных методов формулы итерационного
процесса могут быть получены в следующем виде:
.
Для одношаговых блочных методов формулы итерационного
процесса могут быть получены в следующем виде:
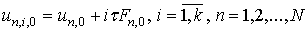
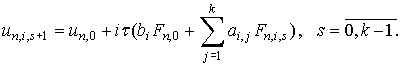
|
(11)
|
Локальная ошибка в узлах блока будет иметь порядок O(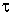 k+2).
k+2).
При численном решении задачи Коши для сравнительной
характеристики методов можно рассматривать различные показатели.
В случае произвольной правой части уравнения о трудоемкости
метода естественно судить по числу обращений для вычисления
значений правой части уравнения на каждый узел сетки.
В качестве одной из оценок степени параллелизма алгоритма
используется коэффициент ускорения [4]: W(k)=T1/Tk,
где T1 – время выполнения алгоритма на
однопроцессорной ЭВМ и Tk – время выполнения
алгоритма на параллельной ВС.
Можно получить оценки времени алгоритма, определяемого
формулами (10) и (11) на одном процессоре.
Если tf – время вычисления значения функции f(t,x),
tad, tmul – время выполнения
операции сложения и умножения соответственно,
то время вычисления по формулам (10) с заданной локальной
точностью составит:
T1, многошаг.=k(2k+1) tf +4k3 tad+ 2k2(2k+1) tmul.
А время вычисления с заданной локальной точностью во всех k узлах блока по формулам (11) составит:
T1, одношаг.=(k2+1) tf +k[k(k-1)+2] tad+ (k3+2k+1) tmul
Для определения Tk возьмем ВС SIMD структуры с топологией кольцо.
Каждый процессорный элемент может выполнить любую арифметическую
операцию за один такт; временные затраты, связанные с обращением
к запоминающему устройству, отсутствуют. Закрепим за каждым узлом блока
процессор. На k процессорах можно одновременно вычислять значения F(s)n,i,
а затем также одновременно получить по формулам значения u(s)n,i
для каждого фиксированного s. Если tta – время передачи
числа соседнему процессору, то время параллельного вычисления
приближенных значений решения с той же точностью для всех узлов блока
составит:
Tk, многошаг.=2(k+1) tf +2[k(2k+1)+1] tad+3[k(2k+1)+1] tmul+k(2k+1) tta.
Tk, одношаг. =(k+1) tf +(k2-k+3) tad+(k2+3) tmul+k(k-1) tta.
Если учитывать только время вычислений правой части уравнений, то ускорение k точечного многошагового параллельного алгоритма можно считать приближенно равным:
W(k)многошаг.=k(2k+1)/(2k+1).
Ускорение параллельного одношагового k точечного алгоритма можно будет теперь считать приближенно равным:
W(k)одношаг.=(k2+1)/(k+1).
В качестве еще одной оценки степени параллелизма алгоритма используется коэффициент эффективности,
который определяется отношением ускорения к числу используемых процессорных
элементов, т. е. E(k)= W(k)/k. Для рассматриваемого случая: Е(k)=1.
Как можно видеть из представленных выражений, многошаговые методы
эффективнее, чем одношаговые.
Однако, в сравнении с последовательными методами, разностные методы
значительно выигрывают.
2. Реализация многошагового блочного метода на решетке процессоров
В общем случае алгоритм решения задачи Коши для СОДУ
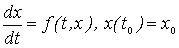
|
(12)
|
многошаговым многоточечным блочным методом [2]
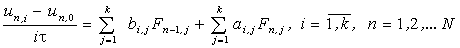
|
(13)
|
где 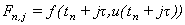
Для вычисления приближенных значений решения задачи Коши (12)
необходимо решить нелинейную систему уравнений. Можно использовать
для этого следующий итерационный процесс:
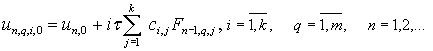
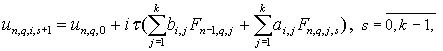
|
(14)
|
который позволяет проводить вычисления параллельно для каждого узла блока.
Пусть начальные приближения для нового блока находятся с помощью
метода Адамса-Башфорта. К началу выполнения расчетов матрицы
коэффициентов уже сформированы.[2]. В качестве модели, на которую
ориентируется решение, используется вычислительная система SIMD
структуры c вычислительным полем 2D-тор, размерностью kxm процессорных
элементов (k – размерность блока, m – размерность системы обыкновенных
дифференциальных уравнений). Каждый процессорный элемент может
выполнить любую арифметическую операцию за один такт; временные затраты,
связанные с обращением к запоминающему устройству, отсутствуют.
Время, определяющее начальную итерацию, будет выражаться как [2]
Tнач.итер.=k*(2tумн+(log2k+1)tсл+(mk-1)tсдв+tp)
Общее время, необходимое на выполнение начального приближения
и на подготовку очередной итерации:
Tнач.итер.+подг.=k*(4tумн+(2log2k+1)tсл+(mk+k-2)tсдв+tp)
Для достижения предельной точности методов необходимо выполнить
k итераций. Поскольку во второй итерационной формуле (14) изменяется
только одно из слагаемых, будем учитывать время, необходимое для
пересчета только этого значения.
Время, которое потребуется для выполнения итераций составит:
Tитер.=k2*(2tумн+(log2k+1)tсл+(mk+k-2)tсдв+tp)
Общее время, за которое может быть получено решение системы уравнений (14) в одном блоке
будет определяться
Tблока=Tнач.итер.+подг.+Титер..
Для оценок качества рассмотренного алгоритма
используются наиболее распространенные критерии [1]:
коэффициент ускорения и коэффициент эффективности.
При расчете значений вектора xn на однопроцессорной
ЭВМ потребуется время, равное:
Tпосл.=mk(2(k+2)tумн+2(k+1)tсл+tp)+mk2((k+2)tумн+2(k+1)tсл+tp)
Если учитывать только время вычислений правой части уравнений, т.к.
времена выполнения арифметических операций и обмена значительно
меньше времени вычисления правой части, то ускорение k
точечного многошагового параллельного алгоритма можно считать
приближенно равным:
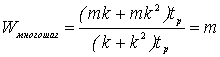
|
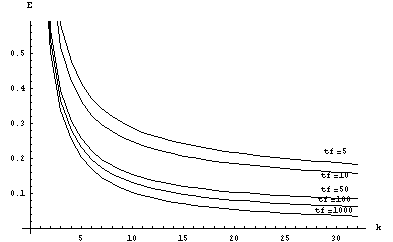
Эффективность k-точечных многошаговых блочных методов
при реализации на SIMD структуре
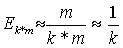
|
|
|
Рисунок 1 – Зависимость эффективности от размерности блока (m=100)
|
|
|
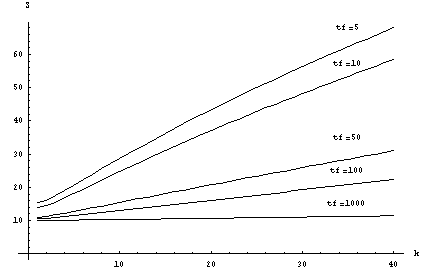
Рисунок 2 – Зависимость ускорения от размерности блока (m=100)
|
Решение СОДУ многошаговым блочным методом довольно
хорошо реализуется на решетчатых структурах. Однако,
как можно видеть по последним двум рисункам, при увеличении
размерности блока эффективность метода падает, что связано
с увеличением времени обмена данными, которое может составлять
большую часть общего времени решения задачи. Поэтому подходить
к выбору структуры вычислительной системы для решения каждой
конкретной задачи необходимо не только с позиций наращивания количества
процессорных элементов, но и оптимизации алгоритмов для сокращения
количества обменов между ними.
3. Реализация многошагового многоточечного блочного метода в SIMD-системах с топологией гиперкуб
В общем случае алгоритм решения задачи Коши для СОДУ,
как уже рассматривалось, многошаговым многоточечным блочным
методом [2] разбивается на следующие подзадачи:
-
вычисление начальных приближений в точках нового блока;
- вычисление правых частей функции для полученных значений;
- подготовка и проведение итерационного процесса в блоке.
Вычисление начальных приближений в точках нового блока
выполняется для каждого блока только один раз и элементарно
распараллеливается, т.к. эти вычисления для каждой точки производятся
независимо, а время вычисления одинаково. Далее производится обмен
вновь полученными значениями, т.е. каждый процессор должен получить
информацию от всех оставшихся, в которых были вычислены значения
элементов вектора начального приближения для блока и, в то же время,
переслать всем процессорным элементам "свое" значение элемента вектора.[5]
После рассылки "все-всем" вычисляются правые части системы
уравнений в каждой точке блока. Относительное время работы
этой части алгоритма сильно варьируется в зависимости от однородности
правых частей системы обыкновенных дифференциальных уравнений
и их сложности.
Подготовка и проведение итерационного процесса в блоке является
самой трудоемкой задачей. Каждый следующий цикл
требует некоторого переупорядочения данных для подготовки
систолического умножения матрицы на вектор, что несет с собой
дополнительные временные затраты. Время работы этой части алгоритма
составляет 85 – 90% от общего. Можно определить необходимые
коммуникационные примитивы:
-
умножение матрицы на вектор. Для этого достаточно "размножить" значения каждого элемента вектора k раз (в соответствии с размерностью блока);
- обмен по типу "все-всем", операции вычисления суммы путем комбинирования операций сдвига и сдваивания произведений правых частей и вспомогательных коэффициентов, распределенных по процессорам.
Время передачи данных между процессорами для используемой
модели можно выразить в виде: [5]
где  – время задержки для подготовительной
работы;
– время задержки для подготовительной
работы;
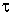 – скорость передачи;
– скорость передачи;
m – число слов в передаваемом такте.
В качестве SIMD-системы была использована разработка фирмы FPS
серии T в области архитектур с массовым параллелизмом. [5]
Для первого способа под каждое уравнение системы будет выделяться
k2 процессорных элементов.
При втором способе размещения данных за каждой точкой блока
закрепляется только один процессор.
Тогда для первого алгоритма величина или m/p/k2 – количество
"тактов", за которые можно рассчитать всю систему для блока из k точек.
Поскольку для нормального функционирования в алгоритме не предусмотрено
обращение к внешней машине, можно принять, что время выполнения одной
операции соизмеримо с временами tсл=tумн=tсдв.
Тогда время, необходимое для расчета значений в одном блоке можно
будет оценить как
Для второго способа расположения данных, а именно, когда для расчета
каждой точки блока выделяется только один процессор, а на каждое
уравнение системы k процессоров, общее время будет определяться как:
Для таких способов размещения данных характеристики параллелизма
можно представить с помощью графиков. [5]
Значения предельных показателей ускорения (W) и эффективности (E)
приведены в таблице 1.[5]
Таблица 1 – Основные показатели параллелизма реализованных методов для SIMD
систем
| №
|
Топологическое соединение
|
Нелинейные системы W |
Нелинейные системы E
|
Линейные системы W
|
Линейные системы E |
| 1.
|
1D- тор (p>=k)
|
~k
|
~1
|
~k
|
~1
|
| 2.
|
1D- тор (p>=m)
|
~k
|
~k/m (m>=k)
|
~m
|
~1
|
| 3.
|
2D- тор (p>=kxk)
|
~k
|
~1/k
|
~kxk/log2k
|
~1/log2k
|
| 4.
|
2D- тор (p>=mxk)
|
~k
|
~1/m
|
~mxk/log2m
|
~1/log2m
|
| 5.
|
3D-тор (p>=kxkxm)
|
~k
|
~1/(mxk)
|
~kxkxm/log2(k+m)
|
~1/log2(k+m)
|
| 6.
|
Гиперкуб (p>=kxk)
|
~k
|
~1/k
|
~kxk/log2(k-1)
|
~1/log2(k-1)
|
Для способов коммутации 2D-, 3D-тор и гиперкуб приемлемые показатели
ускорения и эффективности блочных алгоритмов достигаются только
для случая линейных систем в связи с невозможностью выполнения разнотипных
операций.
Заключение
В представляемой статье проведен анализ существующих параллельных
блочных алгоритмов решения задачи Коши для обыкновенных
дифференциальных уравнений. Данные методы не требуют вычисления
значений в промежуточных точках, что значительно повышает эффективность
счета.
Приведены оценки параллелизма предлагаемых методов:
ускорение и эффективность для различных типов решаемых
систем обыкновенных дифференциальных уравнений.
Также проведен анализ реализации многошагового многоточечного
блочного метода решения задачи Коши для СОДУ в SIMD-системах
с топологией решетка и гиперкуб. Приведены основные показатели
параллелизма рассматриваемых методов для SIMD систем.
Разностные методы являются гораздо более эффективными в сравнении
с известными последовательными методами,
отображенными на параллельные структуры.
Коэффициент эффективности рассматриваемых методов приблизительно равен 1.
Показано, что нужно при решении задачи разностными методами необходимо
выбирать оптимальную размерность блока и структуру параллельной ВС,
иначе эффективность метода падает и увеличивается общее время вычислений.
Литература
-
Системы параллельной обработки: Пер. с англ./ Под. ред. Ивенса Д.– М.: Мир,1985–416с.
- Дмитриева О.А. Параллельные блочные многошаговые алгоритмы численного решения систем обыкновенных дифференциальных уравнений большой размерности. //Науковi працi Донецького державного технiчного університету. Серiя: Проблеми моделювання та автоматизації проектування динамічних систем, випуск 15: – Донецк:, 2000. С. 53–58.
- Фельдман Л. П. Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с сосредоточенными параметрами //Науковi працi Донецького державного технiчного унiверситету. Серiя: Проблеми моделювання та автоматизації проектування динамічних систем, випуск 15: – Донецк:, 2000. С. 12–16.
- Фельдман Л.П., Дмитриева О.А. Разработка и обоснование параллельных блочных методов решения обыкновенных дифференциальных уравнений на SIMD-структурах. //Научн. тр. Донецкого государственного технического университета. Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 29. – Севастополь: "Вебер", 2001. – С. 70–79.
- Дмитриева О.А. Модели отображения многошаговых алгоритмов на параллельные вычислительные системы с топологией гиперкуб//Науковi працi Донецького державного технiчного унiверситету. Серiя: Проблеми моделювання та автоматизації проектування динамічних систем, випуск 15: – Донецк:, 2000. С. 23–26.
-
www.parallel.ru
Информационно-аналитический центр по параллельным вычислениям.
Назад
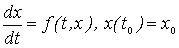
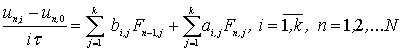
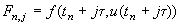 .
.
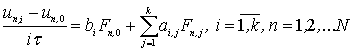
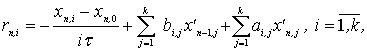
 ,
,  ,
, 
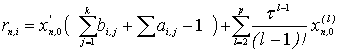
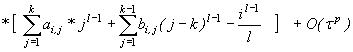
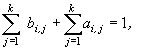
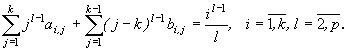
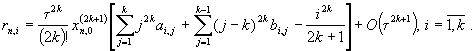
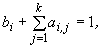
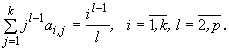
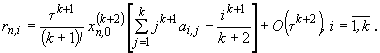
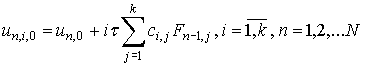
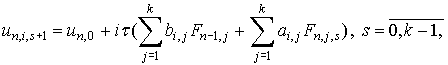
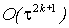 .
Для одношаговых блочных методов формулы итерационного
процесса могут быть получены в следующем виде:
.
Для одношаговых блочных методов формулы итерационного
процесса могут быть получены в следующем виде:
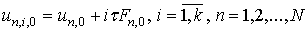
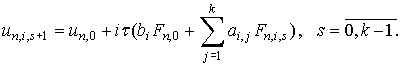
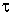 k+2).
k+2).
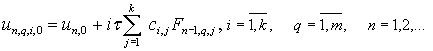
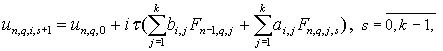
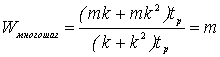
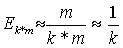


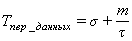
 – время задержки для подготовительной
работы;
– время задержки для подготовительной
работы;