Одной из основных мер связи в корреляционном анализе является линейный коэффициент корреляции.
Парный линейный коэффициент корреляции. С помощью парного линейного коэффициента корреляции измеряется теснота связи между двумя признаками. Линейный коэффициент корреляции чаще всего рассчитывается по формуле
где xi и yi — значения признаков х и у соответственно
для i-ro объекта, i=1, .., n; n — число объектов; 
и 
— средние
арифметические значения признаков х и у соответственно.
Линейный коэффициент корреляции изменяется в пределах от —1 до +1. Равенство коэффициента нулю свидетельствует об отсутствии линейной связи. Равенство коэффициента —1 или +1 показывает наличие функциональной связи. Знак «+» указывает на связь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «—» — на связь обратную (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).
Пример 1. Используя данные табл. 1, рассчитаем коэффициент корреляции между доходом крестьянского хозяйства и стоимостью имеющегося в этом хозяйстве скота
Воспользуемся формулой (6.3), а промежуточные расчеты сделаем с помощью рабочей табл. 1, в которую введем необходимые для вычислений графы:
Как оценить полученное значение коэффициента корреляции? Велико оно или мало? О наличии или об отсутствии связи свидетельствует? Для ответа на эти вопросы проводят проверку значимости коэффициента.
Проверка значимости парного линейного коэффициента корреляции. Коэффициенты корреляции, как правило, рассчитываются для выборочных данных. Чтобы распространить полученные частные результаты на генеральную совокупность, приходится допустить некоторую ошибку, которую можно оценить с помощью средней квадратической ошибки. Средняя квадратическая ошибка для парного линейного коэффициента корреляции достаточно большой выборки вычисляется по формуле
где ρ — коэффициент корреляции генеральной совокупности; n — объем выборки.
В математической статистике доказано, что если признаки х и y распределены по нормальному закону, то в достаточно больших выборках коэффициенты корреляции можно считать распределенными нормально со средним значением ρ и средним квадратическим отклонением σr (нормальное распределение рассмотрено в гл. 4). Этот факт используется для построения доверительных интервалов коэффициента корреляции в генеральной совокупности, а также для проверки значимости выборочных коэффициентов корреляции, т. е. для проверки того, могло ли данное значение r получиться в выборке из некоррелированной генеральной совокупности (ρ=0) в силу простой случайности.
Очевидно, чем больше отклонение r от ρ, тем менее вероятно, что оно
случайно. Так, для нормального распределения вероятность того, что выборочное
значение r отличается от ρ больше чем на 3σr, меньше 0,01, т. е.
величина нормированного отклонения 
может
превысить значение 3 лишь в одном случае из ста. Таким образом, для проверки
значимости r, задаваясь значением вероятности Р (например, Р=0,99), находят по
табл. 1 приложения крити ческое значение tкр (в данном случае
tкр=3) и сравнивают с ним фактическое значение tф где
для ρ=0
Если 
, т. е. происходит маловероятное событие, предположение о
некоррелированности признаков необосновано и коэффициент корреляции считается
значимым. Если же 
, коэффициент корреляции считается незначимым.
Пример 2. Выясним, является ли значимым коэффициент корреляция между доходов крестьянского хозяйства и стоимостью скота в хозяйстве.
В нашем примере, задавшись степенью достоверности Р, равной 0,99 и найдя соответствующее ей в таблице 1 приложения значение tкр=2.58, проводим сравнение. Поскольку tф=0.62/0,18=3,44 заметно превосходит табличное значение 2,58 и вероятность того, что это случайность, мала (0,01), связь между доходом крестьянского хозяйства и стоимостью имеющегося в нем скота следует признать значимой.
Поскольку вычисленный в примере 1 линейный коэффициент корреляции имеет положительный знак, то взаимосвязь между признаками прямая: чем больше скота в хозяйстве, тем больше доход, и чем меньше скота, тем доход меньше.
Заметим, что линейный коэффициент корреляции является показателем взаимной связи между признаками и не дает представления о том, какой из признаков является факторным, а какой — результативным (в формуле (6.3) признаки х и у совершенно равноправны).
Установив существенность взаимной связи между двумя признаками, можно поставить вопрос о тесноте связи. Напомним, что теснота линейной связи измеряется линейным коэффициентом корреляции, но такая оценка верна только для случая, когда расчеты проведены для генеральной совокупности. Для выборочных данных, что обычно имеет место в практике использования корреляционного анализа, необходимо выявить те границы, в пределах которых находится значение коэффициента корреляции генеральной совокупности, т. е. определить для него доверительные интервалы.
Доверительные интервалы для парного линейного коэффициента корреляции. После расчета выборочного коэффициента корреляции (r) и его средней квадратической ошибки (σr) устанавливается уровень достоверности выводов или доверительная вероятность. Для больших выборок соответственно выбранной вероятности Р по таблице нормального распределения определяется параметр t. Верхняя граница интервала получается прибавлением к выборочному коэффициенту корреляции tσr, нижняя граница—вычитанием tσr. Формула средней квадратической ошибки (6.4) содержит неизвестный на практике генеральный коэффициент корреляции. Обычно в расчетах его заменяют выборочным коэффициентом корреляции.
Пример 3. Определим доверительные интервалы для коэффициента, вычисленного в примере 1.
Полагая доверительную вероятность Р, т. е. вероятность, с которой гарантируются результаты, равной 0,98, находим в табл. 1 приложения соответствующее ей значение t, равное 2,33. Воспользовавшись формулой (6.4), где вместо ρ возьмем выборочный коэффициент корреляции r, равный 0,62, получим значение для средней квадратической ошибки
Поскольку tσr=2.33*0.11=0.26, верхняя и нижняя границы равны соответственно 0,88 и 0,36. Другими словами, с вероятностью 0,98 линейный коэффициент корреляции генеральной совокупности находится в пределах от 0,36 до 0,88.
Важнейшей предпосылкой использования корреляционного анализа является нормальность распределения признаков в генеральной совокупности. Нормальность распределения или, по крайней мере, близость распределения к нормальному необходима для корректного проведения проверки значимости связи и вычисления доверительных интервалов. Методы проверки нормальности распределения см. в гл. 9.
Проверка значимости парного линейного коэффициента корреляции для случая малой выборки. При пользовании формулами (6,4) — (6.5) необходимо учитывать два ограничения. Во-первых, они верны для коэффициента корреляции генеральной совокупности и замена последнего выборочным коэффициентом корреляции является искусственным приемом. Риск заменить генеральный коэффициент корреляции существенно отличным от него выборочным коэффициентом увеличивается с уменьшением объема выборки п. Во-вторых, при выборках небольшого объема распределение выборочного коэффициента корреляции может значительно отличаться от нормального, а нормальность распределения является важнейшим условием корректного использования доверительных интервалов и проверки значимости коэффициентов.
Таким образом, при малых объемах выборок (практически при n<50) изложенная выше методика определения доверительных интервалов и проверки значимости коэффициентов корреляции неприменима (поэтому примеры 2—3 являются в какой-то мере условными). Особенно возрастают требования к объему выборки при высоких, близких к 1, значениях показателя связи генеральной совокупности.
Для
малых выборок проверка значимости коэффициента корреляции осуществляется так:
вычисляется фактическое значение tф
величины t, подчиняющейся распределению Стьюдента:
и сравнивается с табличной или критической величиной tкр, зависящей от числа k=n—2, где n—объем выборки, и от выбранной степени достоверности Р. Если , то приходят к выводу о наличии связи; если tф<tкр, то гипотеза об отсутствии связи не отклоняется.
Пример 4. В трех первых столбцах табл. 2 приведены данные, позволяющие анализировать зависимость различий в размерах отрезков, установленных реформой 1861 г. и соотношением форм эксплуатации по шести губерниям Черноземного центра. Вычислим линейный коэффициент корреляции между этими признаками и проверим его значимость (у — % отрезков, х — отношение числа оброчных крестьян к числу барщинных).
Рассчитав средние значения признаков ( 
=15,8, 
=0,4) и
сделав промежуточные расчеты в рабочей таблице, вычислим коэффициент
корреляции по формуле (6.3):
Для проверки значимости коэффициента воспользуемся формулой (6.6):
Табличное значение tкр(k) находим в табл. 2 приложения. Оно расположено на пересечении строки с номером k=n—2 и столбца с удовлетворяющей исследователя степенью достоверности результата. Для нашего примера число степеней свободы k=6—2=4. Положив степень достоверности результата Р равной 0,80, на пересечении 4-й строки и соответствующего 0,90 столбца находим tкр( k)=2,13.
Поскольку tф==2,7>t( k)==2,13, с риском ошибиться в 10 случаях из 100 отбрасываем гипотезу об отсутствии линейной связи, т. е. считаем, что связь между размером отрезков и формой эксплуатации крестьян существует.
Понятие о частной и множественной корреляции. С помощью парного линейного коэффициента корреляции выявляется связь между двумя признаками, один из которых можно рассматривать как результативный, другой — как факторный. Но в действительности на результат воздействуют несколько факторов. В связи с этим возникают два типа задач: задачи измерения комплексного влияния на результативную переменную нескольких переменных и задачи определения тесноты связи между двумя переменными при фиксированных значениях остальных переменных. Задачи первого типа решаются с помощью множественных коэффициентов корреляции, задачи второго типа — с помощью частных коэффициентов корреляции.
Частный, или чистый, коэффициент корреляции между двумя признаками при исключении влияния третьего признака (обозначим его символом r12.3) рассчитывается по формуле (Существует алгоритм, позволяющий вычислить частные коэффициенты корреляции при исключенном влиянии двух, трех и т. д. факторов. Этот рекуррентный алгоритм используется в машинном варианте (есть стандартные программы для ЭВМ).)
где индексы при r показывают номера признаков, связь между которыми оценивается.
Частный коэффициент корреляции первого и второго признаков при исключении влияния третьего оценивает тесноту линейной корреляционной связи между первым и вторым признаками при фиксированном значении третьего признака. Другими словами, он оценивает влияние на результативный (первый) признак изменения лишь второго признака.
Оценка влияния на результативный признак изменений третьего признака при постоянных значениях второго признака определяется по формуле
Значения частных коэффициентов корреляции заключаются в тех же пределах от —1 до +1, что и значения парных коэффициентов корреляции, и так же интерпретируются.
Пример 5. На основе данных табл. 1 оценить, какое из направлений хозяйства — скотоводческое или земледельческое — определяет доход в зажиточной группе крестьян.
Для решения этого вопроса в дополнение к рассчитанному в примере 1 коэффициенту r12, показывающему тесноту взаимосвязи между доходом хозяйства и стоимостью скота в нем, вычислим еще два парных коэффициента корреляции: r13—коэффициент связи между доходом, крестьянского хозяйства и уровнем землепользования в нем, r23 — коэффициент связи между землепользованием крестьянского двора и стоимостью всего скота.
Получим r12=0,62, r13=0,52, r23=0,74. Парные коэффициенты корреляции, показывающие тесноту связи между доходом и уровнем землепользования, между доходом и стоимостью скота, почти равны по величине. Отсюда можно сделать вывод о том, что ни та, ни другая формы хозяйствования не имеет преимущественного влияния на доход. Однако взаимосвязь между самими факторными признаками, т. е. между землепользованием и стоимостью скота (r23), оказалась довольно тесной. Наличие же связи между факторными признаками может искажать действительную тесноту связи между результативным и факторными признаками. Расчет частных коэффициентов корреляции позволяет избавляться от этих искажений. Воспользовавшись формулами (6.7) и (6.8), вычислим коэффициенты r12.3 и r13.2.
Частный коэффициент корреляции между доходом крестьянского двора и стоимостью скота при постоянном показателе землепользования меньше, чем соответствующий парный коэффициент корреляции (0,41 против 0,62). По-видимому, взаимная зависимость между величиной дохода и стоимостью скота частично опосредствовалась через воздействие уровня землепользования.
Частная корреляция между доходом и землепользованием совсем мала (0,12) при довольно большом значении парного коэффициента (0,52). Это можно объяснить тем, что взаимная зависимость дохода и землепользования в значительной степени были усилена влиянием исключенного здесь фактора — стоимости скота.
Таким образом, частные коэффициенты корреляции позволяют установить тесноту взаимосвязи между двумя признаками при исключении влияния других переменных, но для окончательных выводов необходима проверка уровня значимости частных коэффициентов корреляции.
Значимость частных коэффициентов корреляции зависит не только от величины выборочного коэффициента и объема выборки, но также и от числа введенных в исследование переменных.
Для проверки значимости частных коэффициентов корреляции вычисляют величину по формуле
где rij.k — коэффициент корреляции между i и j признаками при исключенном влиянии k-го признака; m—количество исключенных признаков, и сравнивают ее с табличным или критическим значением, соответствующим принятому уровню значимости.
Наличие связи подтверждается, если вычисленное значение tф превосходит значение tкр.
Пример 5 (продолжение). Проверить значимость частных коэффициентов корреляции, рассчитанных выше.
Воспользовавшись формулой (6.9), вычислим величины t1ф для r12.3 и t2ф для r13.2:
Для того чтобы найти табличные значения tкр, нужно задаться степенью достоверности выводов и учесть число n—2—m, фигурирующее в формуле (6.9).
Табличное значение tкр находится по табл. 2 приложения на пересечении строки с номером (n —2—m) и столбца, соответствующего заданной степени достоверности выводов.
В нашем примере в каждом коэффициенте число признаков, от которых мы абстрагируемся, равно 1 и, следовательно, n —2—m=31—2—1==28. Задавшись степенью достоверности, равной 0,90, по табл. 2 приложения находим значение tкр, равное 1,7.
Поскольку t1ф>tкр, подтверждается наличие взаимосвязи между доходом и стоимостью скота. Для второго из рассматриваемых коэффициентов t2ф<tкр, что свидетельствует, по-видимому, об отсутствии непосредственной связи между доходом и землепользованием.
Множественный, или совокупный, коэффициент корреляции для
случая трех признаков, один из которых — результативный (с номером 1) и
два—факторных (с порядковыми номерами 2 и 3) рассчитывается по формуле (Для расчетов используется такая формула
где подстрочные индексы при r показывают номера признаков, связь между которыми оценивается этим коэффициентом корреляции.
Множественный коэффициент корреляции является показателем тесноты линейной связи между результативным признаком и совокупностью факторных признаков.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Равенство его нулю говорит об отсутствии линейной связи, равенство единице—о функциональной связи. Указаний на то, является ли связь прямой или обратной, коэффициент не дает.
Пример 6. Рассчитать множественный коэффициент корреляции между величиной дохода крестьянского хозяйства и совокупным влиянием на него уровня землепользования и стоимости скота в хозяйстве.
Воспользуемся результатами предыдущих примеров: r12=0.62; r13=0.52; r23=0.74. По формуле (6.10);
т. е. степень тесноты связи между доходом крестьянского хозяйства и совокупностью двух факторных признаков составляет 0,63.
Вопрос о значимости множественного коэффициента корреляции решается с помощью так называемого F-критерия. Величина Fф, рассчитанная по специальной формуле, сравнивается с табличным (критическим) значением Fкр — распределения Фишера, соответствующим выбранной степени достоверности Р (или уровню значимости α=1—Р). Если Fф>Fкр, то коэффициент признается значимым на уровне а, так как вероятность того, что Fф для выборки случайно получилось больше Fкр, мала (меньше α). Для случая двух факторных признаков величина вычисляется по формуле (Формула расчетной величины F для общего случая m факторных признаков имеет вид
где R1.23…m+1—множественный коэффициент корреляции; n—число объектов, для которых приводятся значения признаков; m — число факторных признаков. Этот же критерий используется для проверки значимости регрессии, см. (6.20).)
Пример 6 (продолжение). Проверить значимость вычисленного в примере 6 множественного коэффициента корреляции для уровня значимости α=0,05 (P=0,95).
Воспользуемся формулой (6.11):
В табл. 4А приложения (соответствующей α=0,05) во 2-м столбце и 28-й строке (номер столбца определяется по первому числу в квадратной скобке при F, а номер строки—по второму числу) находим критическое значение –распределения. Поскольку при достоверности вывода, равной 0,95, Fкр=3,34, т. е. Fф>Fкр, совместное влияние на величину дохода уровня землепользования и стоимости скота имеет место.
Коэффициент детерминации. Линейный коэффициент корреляции оценивает тесноту взаимосвязи между признаками и показывает, является ли связь прямой или обратной. Но понятие тесноты взаимосвязи часто может быть недостаточным при содержательном анализе взаимосвязей. В частности, коэффициент корреляции не показывает степень воздействия факторного признака на результативный. Таким показателем является коэффициент детерминации (обозначим его D), для случая линейной связи представляющий собой квадрат парного линейного коэффициента корреляции (D=r2) или квадрат множественного коэффициента корреляции. Его значение определяет долю (в процентах) изменений, обусловленных влиянием факторного признака, в общей изменчивости результативного признака.
Пример 7. Рассчитать по данным примера 4 (табл. 2) коэффициент детерминации.
Коэффициент корреляции равен 0,80. Коэффициент детерминации составляет: D=0,802•100%=64%.
Таким образом, различия в размерах отрезков в губерниях Черноземного центра на 64% определялись различиями в соотношении форм эксплуатации.
Корреляционная таблица. В предыдущем изложении каждый признак был представлен рядом значений. В некоторых случаях удобна другая форма записи исходных данных, в виде корреляционной таблицы.
Корреляционная таблица имеет такое устройство: по строкам располагаются значения одного признака, по столбцам — другого признака. Число, стоящее в клетке на пересечении i-й строки и j-го столбца, показывает, как часто i-e значение первого признака встречается совместно с j-м значением второго признака.
В табл. 3 представлены сведения об уходящих в отставку дворянах (60-е годы XVIII в.). В строках дан возраст ухода в отставку, в столбцах — имущественное обложение уходящих в отставку, характеризуемое числом принадлежащих им крестьян. В клетках представлены числа, показывающие, как часто встречаются соответствующие сочетания количественных значений этих двух признаков.
Корреляционная таблица является удобной формой представления данных. Уже беглое знакомство с ней нередко позволяет судить о тесноте связи (не обязательно линейной) между признаками. Если большие значения одного признака в основном сочетаются с большими значениями другого признака, а малые—с малыми, т. е. числа концентрируются вдоль диагонали таблицы, то можно говорить о наличии прямой связи. Если малые значения одного признака в большинстве случаев встречаются совместно с большими значениями другого признака, т. е. числа сосредоточены вдоль другой диагонали, то имеется обратная связь. При этом, чем больше концентрация частот вдоль одной из диагоналей, тем теснее связь.
Корреляционное отношение. Когда изучаемая совокупность (в виде
корреляционной таблицы) разбивается на группы по одному (факторному) признаку
х, то для каждой из этих групп можно вычислить соответствующие групповые
средние результативного признака 
. Изменение групповых
средних от группы к группе свидетельствует о наличии связи результативного
признака с факторным, а примерное равенство групповых средних—об отсутствии
связи. Следовательно, чем большую роль в общем изменении результативного
признака 
играет изменение групповых средних (за счет влияния факторного
признака), тем сильнее влияние этого признака. Величина 
(вариация
признака у) складывается из изменения групповых средних, обусловленного
влиянием факторного признака, т. е. из межгрупповой или факторной вариации
(S2факт) и из вариации признака внутри групп,
обусловленной другими причинами, — внутригрупповой или остаточной
(S2ост). Поэтому отношение
является мерой степени влияния факторного признака на результативный. Значение квадратного корня из этого отношения измеряет «направленную связь» (x→y) в общем виде и носит название корреляционного отношения (ηy/x).
Корреляционное отношение вычисляется по формуле
Величины Sфакт2 и Sy2 вычисляются по формулам:
где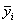 
— среднее значение у в i-й группе; 
— общее
среднее; ni — объем i-й группы; k — количество групп; n — объем
совокупности 
.
Рассмотрим вычисление корреляционного отношения, воспользовавшись данными табл. 3.
Пример 8. В источнике, содержащем данные об уходящих в отставку дворянах, имеются сведения о. причинах ухода в отставку. Как правило, в качестве причины указывалась болезнь. Являлась ли эта причина единственной? Есть основания предположить, что возраст ухода в отставку зависел также от имущественного положения находящихся на военной службе дворян: чем более они были обеспечены, тем с большей легкостью могли оставить службу. Для проверки этого предположения измерим тесноту связи между возрастом уходящих в отставку дворян и их имущественным положением по данным табл. 3.
По признаку имущественного положения совокупность разбита на 4 группы. Рассчитаем средний возраст ухода в отставку для каждой группы
Аналогично вычислим 
, 
, 
. Средние, как мы видим, различны и убывают при переходе из
первой во вторую, из второй в третью, из третьей в четвертую группы. Таким
образом, средний возраст ухода в отставку уменьшается с ростом материальной
обеспеченности, что вполне согласуется с нашей гипотезой о наличии связи между
этими признаками.
Наконец, вычислим общую среднюю арифметическую (средний возраст ухода в отставку по всем данным табл. 3). Для расчета этой средней в качестве весов возьмем числа, стоящие в последнем суммарном столбце таблицы;
Далее, воспользовавшись последовательно формулами (6.13), (6.14) и (6 12), рассчитаем корреляционное отношение:
S2факт=(42,2-40,2)2+(40,8-40,2)2*12+37,7-40,2)2*9+(33,3-40,2)2*3=294,
S2y=(30-40.2)2*12+(40-40.2)2*20+(50-40.2)2*7+(60-40.2)2*3=3098,
Величена корреляционного отношения изменяется в пределах от 0 до 1. Близость ее к нулю говорит об отсутствии связи, близость к единице—о тесной связи.
Корреляционное отношение в отличие от линейного коэффициента корреляции не указывает, является ли связь прямой или обратной. Однако нередко уже по виду исходной таблицы можно решить этот вопрос. Промежуточные расчеты также помогают определить, является связь прямой или обратной: если с ростом факторного группировочного признака растут групповые средние результативного признака, то связь—прямая, если же с увеличением факторного признака значения групповых средних уменьшаются, то связь—обратная.
Как показатель тесноты связи корреляционное отношение имеет более универсальный характер, чем линейный коэффициент корреляции, поскольку его использование не ограничивается случаями линейной связи, а факторный признак может быть не количественным, а ранговым и даже номинальным.
Квадрат корреляционного отношения, выраженный в процентах, и коэффициент детерминации, как он определен выше, имеют одинаковый смысл, только при расчете коэффициента детерминации используется предположение о линейной связи между факторным и результативным признаками, тогда как при вычислении корреляционного отношения вопрос о форме связи не ставится.
Возвращаясь к примеру 8, оценим полученные в нем результаты. Корреляционное отношение, выражающее степень тесноты связи, оказалось равным 0,31, а квадрат корреляционного отношения в процентах (коэффициент детерминации) —9,9%.
Таким образом, возраст ухода в отставку зависит от имущественного положения, но в целом в небольшой степени: колебания имущественного положения только на 9,9% объясняют колебания возраста ухода в отставку. Причем, поскольку с увеличением количества крестьян у владельцев средний возраст ухода в отставку уменьшается, то связь между этими признаками — обратная.
Линейный коэффициент корреляции, как уже отмечалось, является показателем взаимной связи между признаками, но не указывает, какой из них результативный, а какой — факторный. В этом отношении от него выгодно отличается корреляционное отношение, которое позволяет выявить это соотношение. Для этого вычисляются два корреляционных отношения, сравнение которых и помогает определить правильное распределение «ролей» между признаками.
Коэффициент корреляции и корреляционное отношение являются эффективным средством выявления связи между различными количественными признаками и определения ее тесноты. Коэффициент детерминации дает представление и о степени воздействия одних факторов на другие. Однако решение вопроса о тесноте связи нередко упирается в вопрос о форме связи. Кроме того, знание формы связи дает развернутое представление о влиянии различных факторов на результативный признак, а также возможность прогнозирования изменений результата при тех или иных комбинациях значений факторов.
Выявление формы связи осуществляется с помощью методов регрессионного анализа.