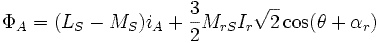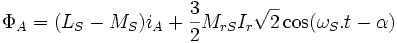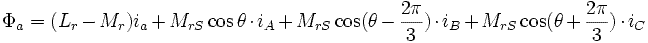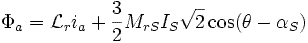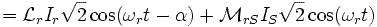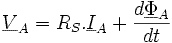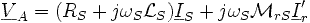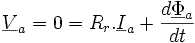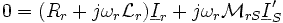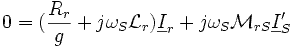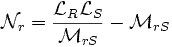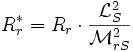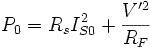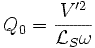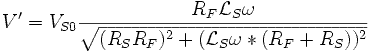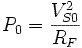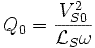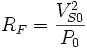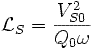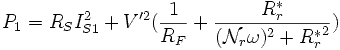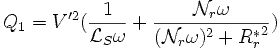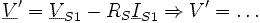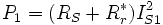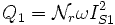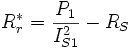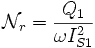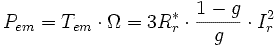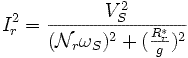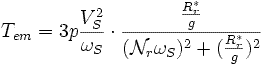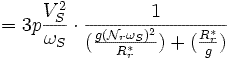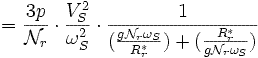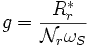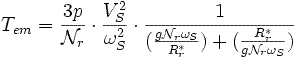Un article de Wikipédia, l'encyclopédie libre.
Une machine asynchrone est une machine à induction,
c'est-à-dire à courant alternatif et
sans connexion entre le stator et le rotor. La dénomination
moteur à induction est parfois utilisée mais ce terme est
d'origine anglo-saxonne.
Présentation
La machine se compose de deux pièces principales :
- Le stator est relié au réseau
- Le rotor est constitué de conducteurs en court circuit qui sont parcourus par des courants induits par le champ magnétique créé par les courants statoriques.
Cette machine peut, selon sa construction, etre reliée à un réseau monophasé ou polyphasé (généralement triphasé car c'est celui de la distribution)
La machine asynchrone est la machine électrique la plus utilisée dans le domaine des puissances supérieures à quelques kilowatts car elle offre alors le meilleur rapport qualité prix. Surtout depuis l'apparition dans les années 1980 de variateurs permettant de faire varier la fréquence de rotation du moteur dans une large gamme.
Bien que réversible, La machine asynchrone est principalement (mais pas exclusivement) utilisée en moteur.
Principes généraux
Les courants statoriques créent un champ magnétique tournant dans le stator. Ce champ tournant est synchrone de la fréquence des courants statoriques, c'est-à-dire que sa fréquence de rotation (sa vitesse) est proportionnelle à la fréquence de l'alimentation électrique. La vitesse de ce champ tournant est appelée vitesse de synchronisme.
L'enroulement au rotor est donc soumis à des variations de flux (du champ magnétique). Une force électromotrice induite apparait qui crée des courants rotoriques. Ces courants sont responsables de l'apparition d'un couple de forces de Laplace qui tend à mettre le rotor en mouvement afin de s'opposer à la variation de flux : loi de Lenz. Le rotor se met donc à tourner pour tenter de suivre le champ statorique.
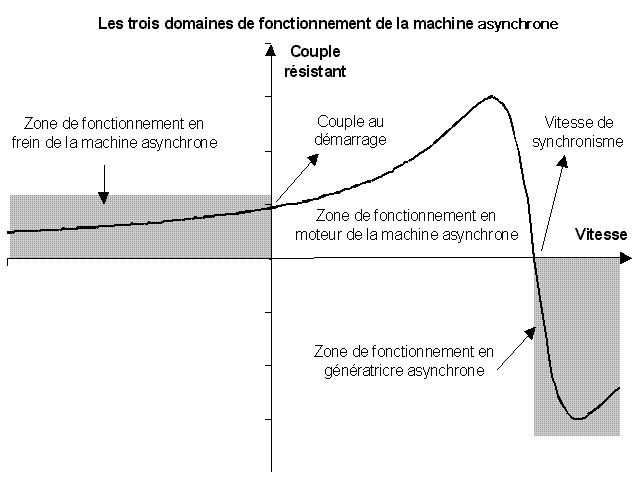
La machine est dite asynchrone car elle est dans l'impossibilité, sans la présence d'un entrainement extérieur, d'atteindre la meme vitesse que le champ statorique. En effet, dans ce cas, les courants s'annulent de meme que le couple qu'ils produisent et la machine n'est plus entrainée. La différence de vitesse entre le rotor et le champ statorique est appelée glissement.
Lorsqu'il est entrainé au-delà de la vitesse de synchronisme, fonctionnement hyper synchrone, La machine devient un alternateur. Mais son stator doit etre forcément relié au réseau car lui seul peut créer le champ magnétique nécessaire pour faire apparaitre les courants rotoriques.
Un fonctionnement en alternateur autonome est toutefois possible à l'aide de condensateurs connectés sur le stator, à condition qu'il existe un champ magnétique rémanent. On retrouve cette meme problématique lorsqu'on cherche à faire fonctionner des machines à courant continu à excitation série en génératrice. à défaut, des dispositifs d'électronique de puissance et une batterie permettent d'amorcer le fonctionnement en génératrice autonome. Cette solution est mise en oeuvre pour produire de l'électricité à l'aide d'éoliennes dans des sites isolés.
Glissement d'une machine asynchrone
- On désigne par
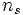 la fréquence de synchronisme, c'est à dire la fréquence de rotation du
champ statorique dans la machine.
la fréquence de synchronisme, c'est à dire la fréquence de rotation du
champ statorique dans la machine.
- On désigne par
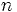 la fréquence de rotation de la machine.
la fréquence de rotation de la machine.
La fréquence de synchronisme est toujours un sous multiple entier de la fréquence du secteur
- en 50 Hz c'est un sous multiple de 3000 tr/min soit : 3000 ; 1500 ; 1000 ; 750 ; etc.
- en 60 Hz c'est un sous multiple de 3600 tr/min, soit : 3600 ; 1800 ; 1200 ; 900 ; etc.
Soit 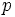 le nombre de paires de poles de la machine et
le nombre de paires de poles de la machine et 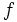 la
fréquence de l'alimentation. On a :
la
fréquence de l'alimentation. On a :
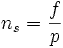 en tr/s ou
en tr/s ou 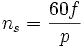 en tr/min.
en tr/min.
Le glisssement correspond à la différence de vitesse entre le
rotor et le champ statorique exprimée sous la forme d'un pourcentage de la
vitesse de synchronisme.
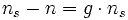 ,
soit
,
soit 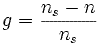
Le glissement est toujours faible, de l'ordre de quelques pour-cent : de 2 % pour les machines les plus grosses à 6 ou 7 % pour les petites machines triphasées, il peut atteindre 10 % pour les petites machines monophasées.
Plaque signalétique d'un moteur asynchrone
| Mot 3~ 50/60Hz | IEC34 | IP55 |
|---|---|---|
| MT90L24-4 | ||
| 1.5/1.75Kw | 1420/1710tr/min | |
| 380-420/440-480VY | 3.7/3.6A | |
| 220-240/250-280VD | 6.4/6.3A | |
| cos phi=0.75/0.78 |
| Moteur triphasé utilisable en 50 et 60 Hz | Classement IP (Indice de Protection) |
|---|---|
| Numéro de série du constructeur | |
| Puissance utile nominale | fréquence de rotation nominale |
| Tension entre phase du réseau d'alimentation pour un couplage étoile | Courant de ligne nominal pour un couplage étoile |
| Tension entre phase du réseau d'alimentation pour un couplage triangle | Courant de ligne nominal pour un couplage triangle |
| facteur de puissance au régime nominal |
- Soit on réalise un couplage étoile (le plus fréquent) et on doit prendre en compte les valeurs de tensions et de courants de la troisième ligne, soit on réalise un couplage triangle et on prend en compte celles de la quatrième ligne.
- A l'aide de grandeurs électriques fournies : tensions entre phases, intensités des courants de ligne et facteur de puissance, il est possible de calculer la puissance absorbée et d'en déduire le rendement de la machine fonctionnant au régime nominal.
-
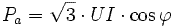 et
et 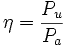
Machine asynchrone triphasée
Constitution
Réalisation du stator
Il est constitué d'un cylindre ferromagnétique entaillé d'encoches permettant d'y loger les bobinages. Ce cylindre est constitué d'un empilement de plaques de tole afin de limiter les courants de Foucault.
Le stator d'une machine triphasée comporte 3 enroulements donc 6 bornes.
- Protection interne des moteurs asynchrones:
On peut réaliser une protection contre les échauffements anormaux des bobinages en placant au coeur de ceux-ci soit un disjoncteur thermique soit une sonde de température qui déclenche un relais de mise en arret, en cas de dépassement d'un seuil déterminé.


Réalisation du rotor
On peut distinguer 3 types de rotor :
- A cage : (rotor en court circuit) : le plus fréquent.
- A cage profonde : permettant un démarrage avec un couple plus important lorsque la machine est alimentée par une source de tension fixe (sans variateur).
- A bague : C'est un rotor bobiné qui a été concu pour permettre de faire varier la résistance du rotor démarrages rotoriques. Ce dispositif a ensuite permis la variation de vitesse avec un rendement acceptable au moyen d'un procédé appelé cascade hyposynchrone. Le cout élevé de ce type de machines et l'apparition des onduleurs à rendu obsolète ce type de machines.
Modélisation et mise en équation
Méthode utilisée
Il est très difficile, pour une charge donnée et à partir des tensions et des impédances, de calculer les courants dans la machine et d'en déduire le couple et la fréquence de rotation.
Comme pour ces labyrinthes que l'on trouve dans les journaux, il est plus facile de partir du but à atteindre et de remonter vers le départ. On considère donc que l'on connait les courants. à partir de l'expression des courants statoriques et rotoriques on déduit les flux du champ magnétique qu'ils produisent. Connaissant les courants et les flux, on écrit l'expression des tensions en appliquant la loi d'Ohm et la loi de Faraday, puis on identifie.
Notations
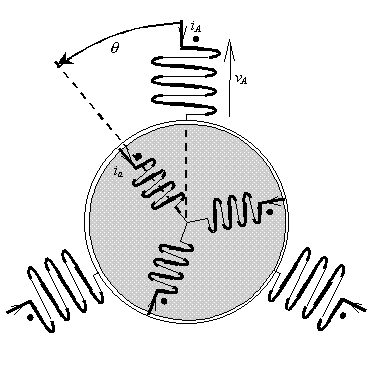
On considère que la machine possède une seule paire de poles.
- Toutes les grandeurs statoriques sont repérées soit par l'indice S soit par des indices en majuscule.
- Toutes les grandeurs rotoriques sont repérées soit par l'indice r soit par des indices en minuscule.
l'angle 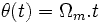 correspond au décalage angulaire entre le stator et le rotor. On a :
correspond au décalage angulaire entre le stator et le rotor. On a :
- l'angle
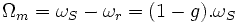
Hypothèses : Son circuit magnétique est homogène et non saturé. Ses diverses inductances sont constantes. Elle est aussi parfaitement équilibrée :
- les courants des trois phases statoriques ont la meme valeur efficace IS.
- les courants des trois phases rotoriques ont la meme valeur efficace Ir.
Les courants
Au stator
On fixe l'origine des temps de manière à ce que l'on puisse écrire :
On en déduit les courants des deux autres phases du stator :
Avec : 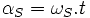 ,
et
,
et 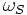 :
pulsation des courants statoriques
:
pulsation des courants statoriques
Au rotor
Avec : 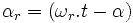 ,
,
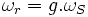 :
pulsation des courants statoriques, et
:
pulsation des courants statoriques, et 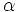 = phase à l'origine de
= phase à l'origine de 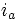 donc variable car l'origine des temps est fixée de par
donc variable car l'origine des temps est fixée de par 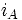 .
.
Les flux
Notations :
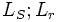 :
Inductances propres d'un
enroulement du stator ; d'un enroulement du rotor.
:
Inductances propres d'un
enroulement du stator ; d'un enroulement du rotor.
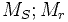 :
Inductance mutuelle entre deux enroulements du stator ; entre deux
enroulements du rotor.
:
Inductance mutuelle entre deux enroulements du stator ; entre deux
enroulements du rotor.
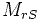 :
Valeur maximale de l'inductance mutuelle entre un enroulement du rotor et un
du stator (correspondant à une position pour laquelle θ = 0 ± 2π/3 .
:
Valeur maximale de l'inductance mutuelle entre un enroulement du rotor et un
du stator (correspondant à une position pour laquelle θ = 0 ± 2π/3 .
Flux à travers un enroulement statorique
On en change rien à cette expression en ajoutant : :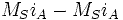
Comme : :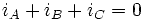
On remplace :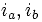 et
et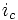 par leurs expressions et on utilise :
par leurs expressions et on utilise :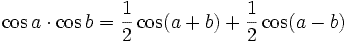
Or 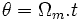 ,
, 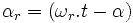 et
et 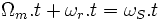
On obtient finalement :
On pose:
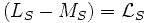 :
inductance cyclique
:
inductance cyclique
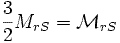 :
inductance mutuelle cyclique
:
inductance mutuelle cyclique
Ces grandeurs cycliques permettent d'isoler chaque phase comme si elle était seule, comme si le flux qui la traverse ne dépendait que du seul courant qui alimente cette phase. L'introduction de ces grandeurs cycliques va permettre d'établir des modèles monophasés équivalents.
On pose également:
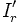 :
Courant fictif de valeur efficace
:
Courant fictif de valeur efficace 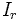 mais de fréquence
mais de fréquence 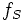
L'expression du flux devient alors très simple. On applique la transformation
complexe et l'on obtient le flux complexe d'une phase du stator:
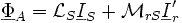 à la pulsation
à la pulsation 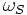
Flux à travers un enroulement rotorique
Le calcul du flux rotorique se mène de manière identique avec une différence de signe.
Avec l'introduction des grandeurs cycliques
Le flux à travers un enroulement rotorique s'écrit:
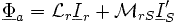 à la pulsation
à la pulsation 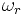
Les tensions
Tension aux bornes d'une phase du stator
Tension aux bornes d'une phase du rotor
Le rotor est en court-circuit.
Comme on a 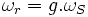 ,
on obtient :
,
on obtient :
Schémas équivalents
Schéma général
Les deux équations suivantes :
correspondent à un schéma équivalent ne comportant que des tensions et des courants ayant une fréquence identique à celle de l'alimentation qui alimente la machine et dont le schéma est le suivant :
Schéma ramené au stator
Les circuits magnétiquement couplés peuvent etre transformés en de nombreux schémas équivalents (pour plus de détails, on se référera à l'article correspondant). Chacune de ces transformations conduit à un modèle possible pour décrire la machine asynchrone. Dans la pratique, seul certains modèles sont effectivement utilisés.
Le modèle à fuites secondaires avec l'ensemble ramené au stator est le plus fréquent dans la littérature car il comporte des éléments que l'on peut identifier relativement simplement et de manière suffisamment précise, et il est simple d'emploi.
avec :
Ces grandeurs ne sont pas calculables (en particulier Rr), mais l'important est de savoir que si l'on admet les hypothèses de départ, alors il existe un dipole identique à celui représenté ci-dessus équivalent à une phase de la machine asynchrone alimentée par un système de tensions triphasées équilibré.
Il est intéressant pour les bilans de puissance de décomposer la résistance
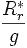 en deux termes :
en deux termes :
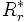 :
résistance ramenée de l'enroulement rotorique, responsable des pertes
par effet Joule au rotor (pertes Joule rotoriques).
:
résistance ramenée de l'enroulement rotorique, responsable des pertes
par effet Joule au rotor (pertes Joule rotoriques).
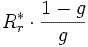 :
résistance fictive : la puissance qu'elle consomme correspond en
réalité à la puissance utile de la phase considérée. (Puissance
transformée en puissance mécanique par la machine).
:
résistance fictive : la puissance qu'elle consomme correspond en
réalité à la puissance utile de la phase considérée. (Puissance
transformée en puissance mécanique par la machine).
Prise en compte des pertes fer
On a considéré que le circuit magnétique était sans pertes, ce qui n'est pas le cas. Pour rendre compte des pertes fer qui dépendent du carré de l'alimentation, on ajoute dans ce modèle une résistance fictive RF en parallèle avec l'inductance statorique.
Identifications des éléments du schéma équivalent
Après avoir établi que le schéma précédent correspondait à une phase de la machine asynchrone, on peut identifier le modèle correspondant à une machine quelconque en réalisant trois essais :
Essai en continu
Réalisé sur une phase de la machine, il permet de mesurer la résistance statorique RS.
Essai au synchronisme : g = 0
1/g tend vers l'infini. Le modèle équivalent d'une phase de la machine devient :
à l'aide d'un wattmètre, d'un ampèremètre et d'un voltmètre, on mesure P0, Q0, IS0 et VS0 on obtient les trois équations :
RS étant connue, on peut calculer les trois
inconnues : RF, 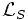 et V'
et V'
Le courant IS0 étant faible lors de l'essai au synchronisme, on peut généralement négliger la perte de tension due à la resistance statorique devant la tension VS0. Les équations deviennent alors:
On calcule alors directement RF et 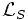 :
:
Essai rotor bloqué et tension réduite : g = 1
g tend vers 1. Le modèle équivalent d'une phase de la machine devient :
A l'aide d'un wattmètre, d'un ampèremètre et d'un voltmètre, on mesure P1, Q1, IS1 et VS1 et on obtient les trois équations :
La tension VS1 étant faible, les courants ciculants dans
RFet 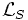 peuvent généralement etre négliger devant IS1. Les équations
deviennent alors:
peuvent généralement etre négliger devant IS1. Les équations
deviennent alors:
L'identification des derniers paramètres de la machine est alors rapide:
Caractéristiques électromécaniques
Le schéma établi précédemment permet d'obtenir facilement les caractéristiques électromécaniques de la machine asynchrone monophasée :
En effet la puissance électromagnétique utile, c'est-à-dire celle transformée
en énergie mécanique correspond pour chaque phase à la puissance consommée par
la résistance 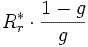
La puissance électromécanique totale a donc pour expression :
Machine alimentée par un système de tensions de fréquence fixe
Le modèle ci-dessus permet d'obtenir l'expression du couple soit en fonction du glissement soit en fonction de la vitesse. Le calcul est très simplifié et peut etre fait à la main si l'on néglige la résistance statorique. Dans ce cas, on ajoute une erreur de 2 ou 3 %, mais on obtient une courbe dont l'allure est proche de la réalité. De toute facon, on ne doit pas perdre de vue que ce ne sont que des modèles.
Dans le cadre de cette approximation on a :
Avec 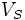 :
valeur efficace de la tension aux bornes d'une des phases du stator de la
machine.
:
valeur efficace de la tension aux bornes d'une des phases du stator de la
machine.
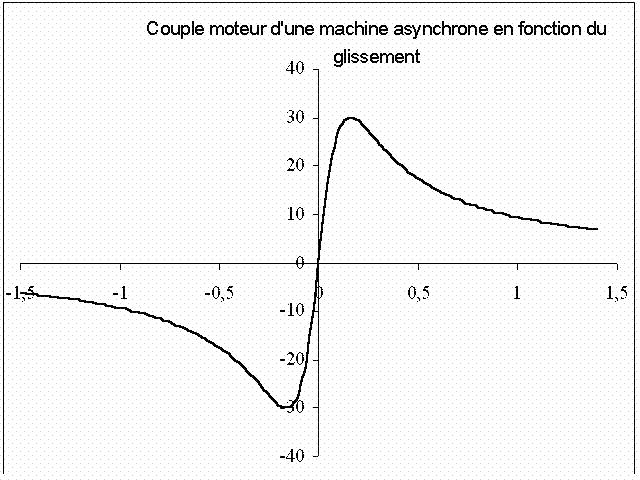
Couple électromécanique en fonction du glissement
De l'expression de la puissance et des deux équations ci-dessus on en déduit l'expression du couple électromagnétique en fonction du glissement g :
Pour une machine à p paires de poles on a : 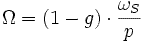
Cela conduit à :
Le couple électromagnétique passe par un maximum pour :
La courbe représentative de l'expression du couple en fonction du
glissement possède une symétrie par rapport à l'origine :
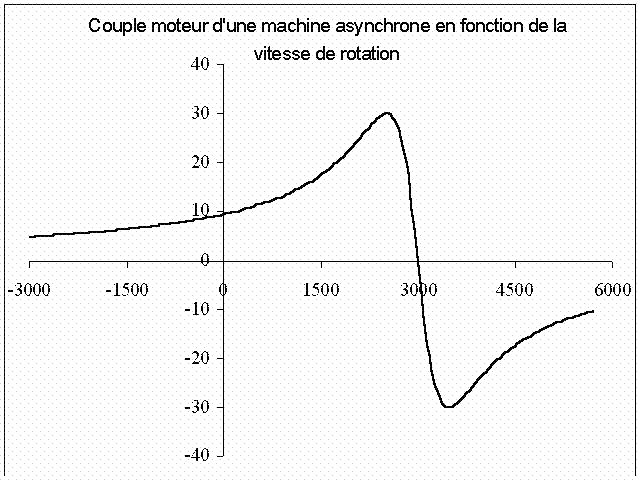
Couple électromécanique en fonction de la vitesse de rotation
Cette courbe est plus habituelle et plus concrète, elle se déduit simplement de la courbe en fonction du glissement grace à la relation :
Les domaines de fonctionnement de la Machine asynchrone
Machine alimentée par un onduleur
Réglage de la vitesse de rotation des moteurs asynchrones triphasés [1]
Les onduleurs les plus répandus sont les onduleurs MLI ( à modulation de largeur d'impulsion) dont le mode de commande permet de garder le rapport U1/f constant et d'obtenir des courants quasiment sinusoidaux. U1 étant la valeur efficace du fondamental.
Commande en U/f
Principe
En régime sinusoidal, la conservation du rapport U/f permet au circuit magnétique d'etre dans le meme état magnétique quelque soit la fréquence d'alimentation. Autrement dit, la forme du cycle d'hystéresis parcourru par le circuit magnétique reste identique quelque soit f.
Ceci a pour conséquence qu'une commande qui maintient U1/f constant, où U1représente la valeur efficace du fondamental, permet de conserver la meme courbe de couple en fonction du glissement pour n'importe quelle fréquence d'alimentation. Les autres harmoniques présents,multiples de 5 et 7, créent des couples pulsants dont la moyenne est nulle.
Pour cela, la machine asynchrone est alimenté par un onduleur délivrant une tension de fréquence f et dont la valeur efficace du fondamental V1 est telle que le rapport V1/f est maintenu constant.
Mise en équation
Pour comprendre le principe de la commande en U/f, il faut reprendre l'équation du couple.
On note Cmax le couple maximum.
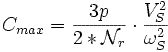
On réécrit la relation flux/tension afin de faire apparaitre le flux.
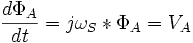
On note Φs la valeur efficace du flux nominal.
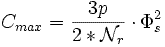
Si on garde le rapport 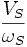 constant, il est donc possible de déplacer la vitesse à laquelle Cmax est disponible.
L'expression du couple devient:
constant, il est donc possible de déplacer la vitesse à laquelle Cmax est disponible.
L'expression du couple devient:
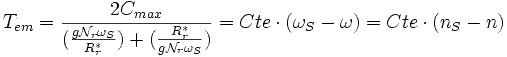
La courbe du couple en fonction de nS - n est unique.
Remarques
Lors d'un démarrage (faible fem) à fort couple (courant important), la chute de tension due à la résistance statorique devient plus importante que la fem. Il est alors impossible d'obtenir le flux nominal dans la machine grace à la loi U/f=cst. Pour compenser cela, les variateurs industriels proposent différentes lois U(f). Le choix de la loi à utiliser dépend de l'application.
Une fois que la tension nominale est atteinte, on augmente la fréquence d'alimentation du moteur sans augmenter sa tension. On parle alors de défluxage de la machine. Cela amène bien entendu une baisse du couple maximum délivrable par la machine. Un démarrage dans de tels conditions se fera donc à couple constant puis à puissance constante.
Inconvénients
Les procédés de variations de vitesse pour les moteurs asynchrones sont générateurs d'harmoniques.
Commande vectorielle
Afin d'améliorer les performances du moteur lors des régimes transtoires, il existe des commandes vectorielles.
<<Íàçàä ê áèáëèîòċêċ



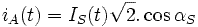
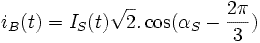
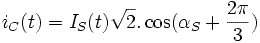
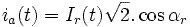
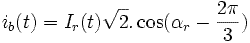
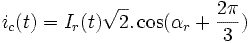
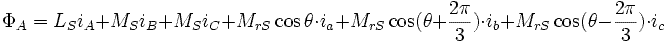
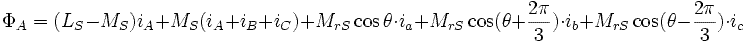
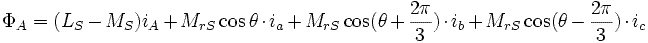
![\Phi_A = (L_S - M_S) i_A + M_{rS} I_r \sqrt{2} \left\{ \frac{3}{2} \cdot \cos (\theta + \alpha_r) + \frac{1}{2} \cdot \left[ \cos (\theta - \alpha_r) + \cos (\theta - \alpha_r - \frac{2 \pi}{3}) + \cos (\theta - \alpha_r + \frac{2 \pi}{3}) \right] \right\}\,](8d69a9b1bf6c2f0839dc40a0a0fd5c7c.gif)