Автореферат выпускной работы магистра

Лысенко Оксаны Анатольевны

Тема работы:

"Математическое моделирование нагрузок в частотно-регулируемых электроприводах двухдвижительного цевочно-реечного механизма перемещения очистного комбайна "

Научный руководитель: профессор кафедры "Горные машины", д.т.н.Кондрахин В. П.

 

ВВЕДЕНИЕ

 

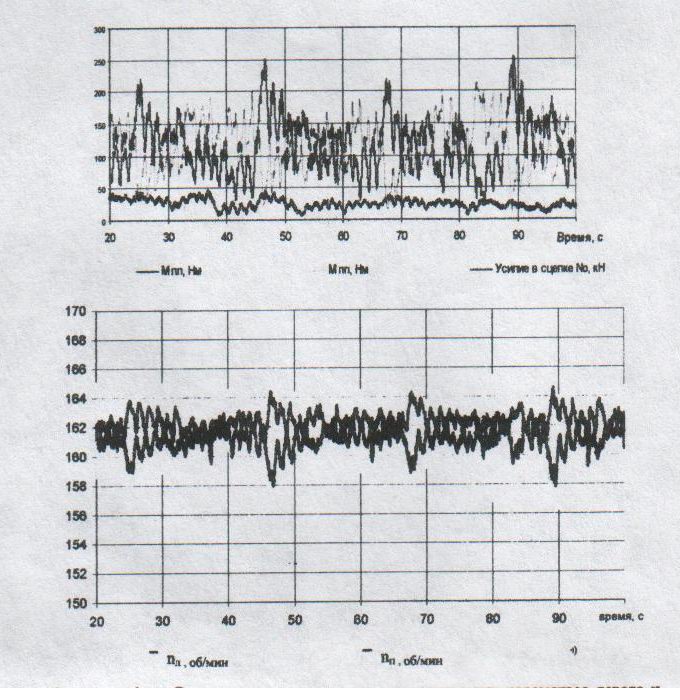
На комбайне УКД300 использован двухдвижительный цевочно-реечный механизм перемещения с частотно-регулируемым электроприводом. Эксплуатация комбайнов УКД300 выявила необходимость повышения тяговых характеристик механизма перемещения. Фактическое суммарное тяговое  усилие двух движителей в некоторых случаях существенно меньше номинального значения. Одна из главных причин этого – неравномерное распределение нагрузки между частотно-регулируемыми асинхронными электроприводами. На специальном стенде на ЗАО «Горловский машиностроитель» проводились экспериментальные исследования комбайна УКД300. В результате анализа исследований установлены основные закономерности формирования динамических процессов в приводах механизма перемещения. На рисунке 1 приведен типичный фрагмент осциллограммы крутящих моментов в приводах левого и правого движителей частоты вращения промежуточных валов редуктора. Во всех зарегистрированных режимах колебания моментов в левом и правом приводах происходят практически в противогазе как по высоко- так и по низкочастотным составляющим. Вследствие этого формируется существенная неравномерность распределения нагрузки между приводами левого и правого движителей. В отдельные моменты времени наиболее нагруженный движитель обеспечивает до 96%  общего тягового усилия. В отдельных случаях возможна работа привода в генераторном режиме.

На осциллограммах крутящих моментов и частот вращения валов следует выделить прежде всего высокочастотную составляющую, период которой обусловлен периодом контакта зуба звездочки  с цевочной рейкой. Наличие такой составляющей позволяет сделать вывод о том, что неравномерность кинематических и силовых параметров вызвана несовершенством геометрических характеристик зацеплений «звезда – цевка» и «колесо – звезда»  в  трехэлементном движителе.

Рисунок 1. - Фрагмент осциллограммы крутящих моментов в приводах левого и правого движителей

 

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

 

Для удобства анализа кинематической картины зацепления введен в рассмотрение приведенный кинематический  r_кi(φ_кi)  радиус i –ого трехэлементного движителя, физический смысл которого ясен из выражения:

                                     (1.1)

где ω_кi – угловая скорость колеса i – ого трехэлементного движителя;

V_П(f_с) – скорость перемещения комбайна, зависящая от частоты питающей сети  f_с;

φ_кi – угол поворота колеса i – ого трехэлементного движителя.

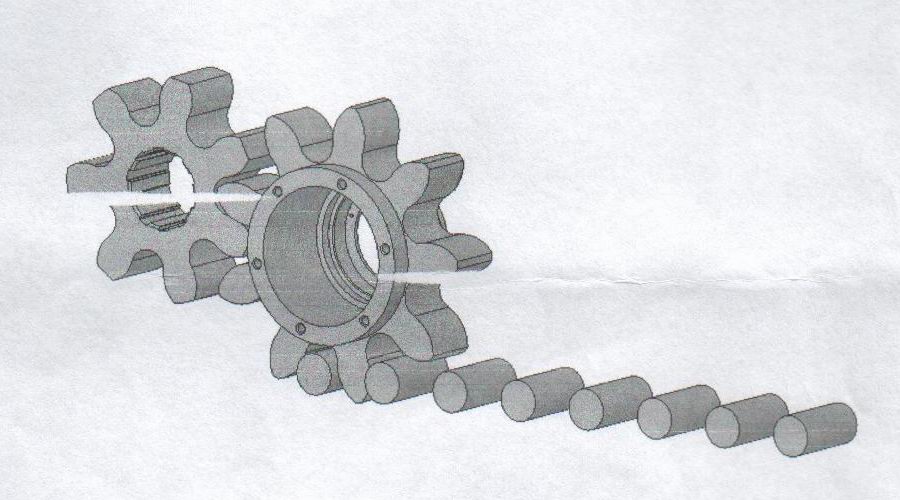
Для экспериментального моделирования использовалась 3D модель созданная при помощи современных программ автоматизированного проектирования.

Рисунок 2. - 3D модель, созданная для экспериментального моделирования

 

Твердотельное моделирование приведенного кинематического радиуса при межосевом расстоянии 147 мм осуществлялось путем фиксирования следующих параметров: линейного перемещения оси колеса и его угла поворота.

Приведенный кинематический радиус:

,

 Но    ,                                    

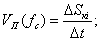
где  – перемещение оси колеса за интервал времени ;

 – угол поворота колеса за интервал времени .

Таким образом,  .

Эксперимент по моделированию приведенного кинематического радиуса при  переходе звезды на новую цевочную рейку с межосевым расстоянием 147 мм был проведен при увеличении расстояния между двумя цевками с 100 мм до 104 мм, что имитировало переход звезды на новую цевочную рейку.

 

ВЫВОДЫ ПО ЭКСПЕРИМЕНТУ

 

На основании проведенных экспериментальных исследований можно сделать следующие выводы:

–приведенный кинематический радиус является периодической функцией, период которых соответствует периоду зацепления звезды с цевкой;

– на графиках приведенного кинематического радиуса четко прослеживается резкое изменение значений, которое обусловлено изменением контактирующей пары в зацеплении «колесо – звезда»;

– увеличение межосевого расстояния в зацеплении «звезда – цевка» оказывает влияние на рост перепада (резкого скачка) значений приведенного кинематического радиуса при переходе с одной цевки на другую (при межосевом расстоянии 147 мм перепад составляет 6 мм);

– на основании графиков, характеризующих процесс прохождения стыка между цевочными рейками, можно сделать вывод о том, что при переходе на новую цевочную рейку уменьшается период зацепления звезды с предыдущей цевкой (примерно на 45 % для межосевого расстояния 147 мм), а период зацепления звезды с первой цевкой новой рейки увеличивается на те же значения;

– различия в характере и численных значениях между данными, полученными в результате натурного эксперимента и твердотельного моделирования, объясняются тем, что твердотельное моделирование не учитывает износа цевочных реек в процессе эксплуатации, а также упругих деформаций, возникающих в элементах трехэлементного движителя.