Автореферат магистерской работы по теме: Обоснование параметров и разработка технических решений в
области частотно-управляемого автоматизированного привода подачи очистного комбайна
Основным технологическим процессом шахты является получение полезного ископаемого с установленными показателями качества.
Применение современных шахтных высокопроизводительных машин и механизмов требует перехода к управлению оборудованием в автоматизированных режимах с целью обеспечения оптимальных условий работы.
Системы перемещения выемочных машин являются теми элементами автоматизированное управление которыми наиболее целесообразно и востребовано.
Ряд известных специалистов в области горного комбайностроения считает наиболее перспективными подсистемы ПВМ на основе частотно-регулируемого электропривода с учетом доводки отечественных преобразовательных станций во взрывозащищенном исполнении до необходимого технического уровня.
Целью и задачами работы является разработка математической модели асинхронного двигателя при управлении частотой и напряжением статора, также составление передаточных функций и структурной схемы асинхронного двигателя при управлении вышеуказанными параметрами. Результатом работы будет общая структурная схема электродвигателя совместно с преобразователем частоты.
Планируемой научной новизной является разработка системы управления частотно-регулируемым электроприводом подачи очистного комбайна на коком - нибудь из микроконтроллеров семейства Atmel.
Практической ценностью будет предполагаемое внедрение разработок в технические образцы очистной техники.
При исследовании переходных процессов в трехфазных асинхронных электродвигателях целесообразно принять следующие допущения, позволяющие в доступной математической форме выразить соотношения основных параметров и координат электродвигателя: 1) намагничивающие силы обмоток двигателя распределены синусоидально вдоль окружности воздушного зазора; 2) потери в стали статора и ротора отсутствуют; 3) обмотки статора и ротора строго симметричны со сдвигом осей обмоток на 120°; 4) насыщение магнитной цепи отсутствует.
Уравнения равновесия напряжений для обмоток трех фаз статора имеют вид
| |
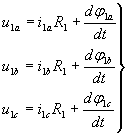 |
(1) |
соответственно для обмоток трех фаз ротора
| |
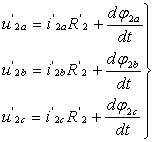 |
(2) |
где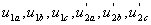 - мгновенные значения фазных напряжений статора и ротора;
- мгновенные значения фазных напряжений статора и ротора;
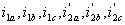 -мгновенные значения фазных токов статора и ротора;
-мгновенные значения фазных токов статора и ротора;
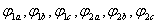 - полные потокосцепления фазных обмоток;
- полные потокосцепления фазных обмоток;
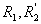 - активные сопротивления обмоток статора и ротора.
- активные сопротивления обмоток статора и ротора.
Асинхронный электродвигатель представляет собой систему магнитно связанных обмоток, расположенных на статоре и роторе. При вращении ротора взаимное положение обмоток статора и ротора непрерывно изменяется, соответственно изменяется и взаимная индуктивность между ними. С учетом принятых допущений можно считать, что взаимная индуктивность пропорциональна косинусу текущего угла между осями обмоток ротора и статора. Полная система уравнений потокосцеплений в обмотках статора и ротора определяется уравнениями
| |
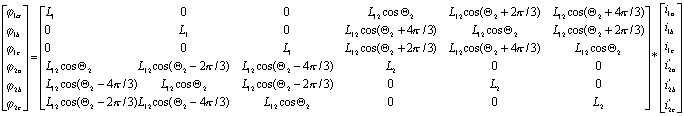 |
(3) |
где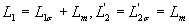 - полные эквивалентные индуктивности фаз статора и ротора, состоящие из индуктивностей от полей рассеяния
- полные эквивалентные индуктивности фаз статора и ротора, состоящие из индуктивностей от полей рассеяния 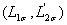 и главного потока
и главного потока 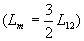 ; L12 — максимальная взаимная индуктивность между любой обмоткой статора и любой обмоткой ротора, которая имеет место при совпадении их осей;Q2 — текущий угол между осями обмоток фаз ротора и статора.
; L12 — максимальная взаимная индуктивность между любой обмоткой статора и любой обмоткой ротора, которая имеет место при совпадении их осей;Q2 — текущий угол между осями обмоток фаз ротора и статора.
Уравнение (3) содержит гармонические коэффициенты, что создает значительные трудности при исследовании переходных процессов. Для того чтобы исключить гармонические коэффициенты, используют преобразования координат. С этой целью реальные переменные статора и ротора заменяются их проекциями на взаимно перпендикулярные оси координат, вращающиеся с произвольной скоростью 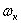 Такое преобразование координат соответствует приведению трехфазного электродвигателя к эквивалентному двухфазному.
Такое преобразование координат соответствует приведению трехфазного электродвигателя к эквивалентному двухфазному.
При математическом описании трехфазных асинхронных электродвигателей удобно оперировать не мгновенными значениями координат, а их результирующими векторами. Если, например, мгновенные значения токов равны 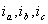 то результирующий вектор тока определяется уравнением:
где
то результирующий вектор тока определяется уравнением:
где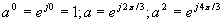
Аналогично определяются результирующие векторы напряжения
и потокосцепления
Используя выражения результирующих векторов, уравнения (1) можно записать в виде одного дифференциального уравнения в векторной форме. Для этого первое уравнение из (1) умножается на 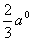 , второе на
, второе на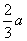 третье на
третье на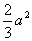 .Суммируя полученные произведения, получим
или в векторной форме
.Суммируя полученные произведения, получим
или в векторной форме
| |
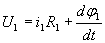 |
(4) |
Аналогично векторное уравнение напряжений ротора:
| |
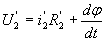 |
(5) |
В уравнениях (4) и (5) векторы записаны соответственно в системах координат статора и ротора. Для совместного решения уравнений их необходимо привести к одной системе координат.
Уравнения асинхронного электродвигателя в системе координат, вращающейся с произвольной скоростью 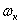 имеют вид
имеют вид
| |
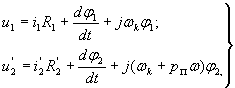 |
(6) |
Где 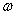 - угловая скорость вращения ротора; рп – число пар полюсов.
- угловая скорость вращения ротора; рп – число пар полюсов.
При исследовании переходных процессов в асинхронном электродвигателе, управляемом частотой и напряжением статора, удобно использовать систему координат, вращающуюся со скоростью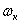 , равной угловой скорости вращения магнитного поля
, равной угловой скорости вращения магнитного поля 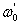 , приведенной к числу пар полюсов, равному единице (приведенной к двухполюсному электродвигателю).
, приведенной к числу пар полюсов, равному единице (приведенной к двухполюсному электродвигателю).
Предполагается при этом справедливым равенство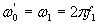
На основании уравнений (6) для рассматриваемой координатной системы можно записать
| |
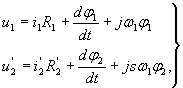 |
(7) |
где s – скольжение электродвигателя: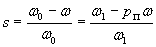 ,(
,( 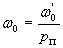 - угловая скорость вращения магнитного поля, или синхронная скорость электродвигателя).
- угловая скорость вращения магнитного поля, или синхронная скорость электродвигателя).
Потокосцепления связаны с токами через индуктивности
| |
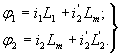 |
(8) |
Для определения электромагнитного момента асинхронного электродвигателя используется векторное произведение 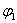 и
и 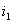 ,тогда
,тогда
| |
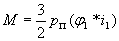 |
(9) |
или векторное произведение 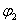 и
и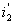 , тогда
, тогда
| |
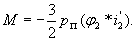 |
(10) |
Учитывая выражения (8), можно записать (9) и (10) в виде
| |
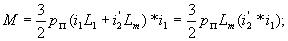 |
(11) |
| |
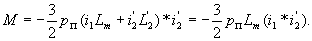 |
(12) |
Вторые равенства в уравнениях (11), (12) справедливы потому, что векторное произведение двух одинаково направленных векторов равно нулю.
Для полного описания переходных процессов в асинхронном электродвигателе к уравнениям напряжений и моментов следует добавить уравнение
| |
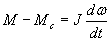 |
(13) |
записанное для скалярных значений моментов М и Мс.
Для дальнейших исследований динамических свойств асинхронных электродвигателей целесообразно результирующие векторы представить в виде проекций на комплексной плоскости и записать их через вещественные и мнимые части в следующем виде:
| |
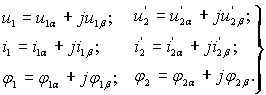 |
(14) |
Совместив вектор напряжения статора с действительной осью координатной системы, т.е. положив 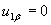 на основании (7) получим
на основании (7) получим
| |
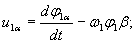 |
(15) |
| |
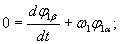 |
(16) |
| |
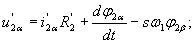 |
(17) |
| |
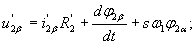 |
(18) |
Выразив также электромагнитный момент по уравнению (9) через составляющие векторов тока и потокосцепления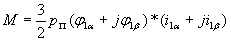 и применив правило векторного произведения векторов, получим абсолютное значение момента:
и применив правило векторного произведения векторов, получим абсолютное значение момента:
| |
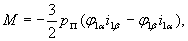 |
(19а) |
где 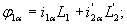 ,
,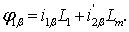
Воспользовавшись выражением (10), можно получить
| |
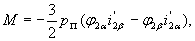 |
(19б) |
где 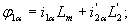 ,
,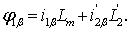
Составляющие тока ротора могут быть выражены через составляющие потокосцепления в следующем виде:
| |
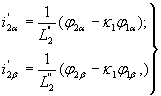 |
(20) |
где к1 – коэффициент электромагнитной связи статора;
| |
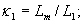 |
(21а) |
| |
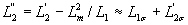 |
(21б) |
С учетом (8) и (21а) можно выражения моментов записать в форме, удобной для вывода передаточной функции двигателя: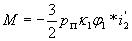 или
или
| |
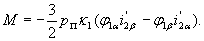 |
(22) |
В случае одновременного изменения частоты и напряжения статора, при котором потокосцепление статора остается постоянным, из уравнений (15) и (16) можно получить
| |
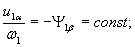 , , 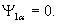 |
(23) |
Для двигателя с короткозамкнытым ротором в уравнениях (17),(18)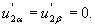 Выразив из уравнении (20)
Выразив из уравнении (20) 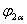 и
и 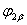 и подставив их в уравнения (17), (18), получим
и подставив их в уравнения (17), (18), получим
| |
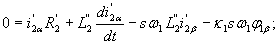 |
(24) |
| |
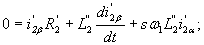 |
(25) |
| |
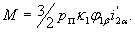 |
(26) |
Рассматривая переменные величины в приращениях относительно начальных значений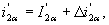 ,
,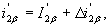 ,
,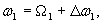 ,
,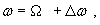 ,
,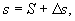 ,
,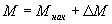 ,получим из (23) – (26) уравнения для статического режима, связывающие начальные значения координат,
,получим из (23) – (26) уравнения для статического режима, связывающие начальные значения координат,
| |
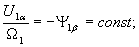 |
(27) |
| |
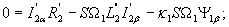 |
(28) |
| |
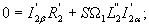 |
(29) |
| |
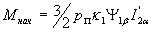 |
(30) |
и уравнения для динамического режима, связывающие приращение координат:
| |
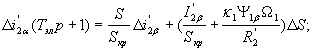 |
(31) |
| |
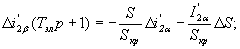 |
(32) |
| |
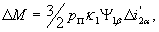 |
(33) |
где 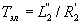 - электромагнитная постоянная электродвигателя;
- электромагнитная постоянная электродвигателя;
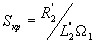 - критическое скольжение.
- критическое скольжение.
На основании уравнений (27)-(33) можно запасать передаточную функцию
| |
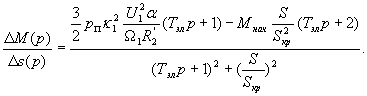 |
(34) |
Выражение 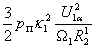 в первом слагаемом числителя (34) представляет собой значение фиктивного пускового момента Мп.ф., определяемое в результате линеаризации рабочей части механической характеристики двигателя для принятых значений напряжения статора
в первом слагаемом числителя (34) представляет собой значение фиктивного пускового момента Мп.ф., определяемое в результате линеаризации рабочей части механической характеристики двигателя для принятых значений напряжения статора 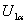 и угловой частоты напряжения статора
и угловой частоты напряжения статора 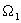 :
:
| |
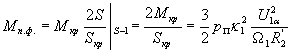 |
(35) |
где 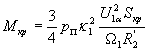 - критический момент двигателя.
- критический момент двигателя.
Момент Мнач. во втором слагаемом числителя (34) можно записать с учетом принятых допущений в виде
| |
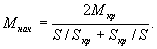 |
(36) |
С учетом (35) и(36) выражение (34) примет вид:
| |
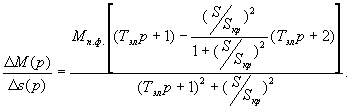 |
(37) |
Для рабочей части механической характеристики двигателя можно принять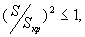 и тогда передаточную функцию (37) можно записать в упрощенном виде
и тогда передаточную функцию (37) можно записать в упрощенном виде
| |
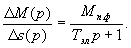 |
(38) |
Представив зависимость скольжения электродвигателя от угловой частоты напряжения статора в приращениях и выполнив линеаризацию при условии, что в рабочей области 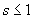 , получим
, получим
| |
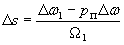 |
(39) |
Уравнения равновесия моментов (13) может быть записано в приращениях в виде
| |
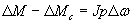 |
(40) |
На основании полученных выражений составим структурную схему асинхронного, двигателя при управлении угловой частотой напряжения статора и при условии постоянства потокосцепления статора. Однако это удобнее сделать, если представить координаты двигателя в о. е., приняв за базовые значения координат их значения в номинальном режиме: Мп.ф.н, 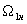 ,
,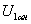 ,
,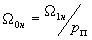 ,где
,где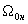 - синхронная угловая скорость двигателя. Тогда
- синхронная угловая скорость двигателя. Тогда
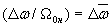 ,
,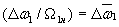 ,
,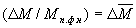 ,
,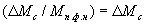 ,
,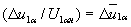 .Передаточная функция (37) с учетом (39) запишется так:
.Передаточная функция (37) с учетом (39) запишется так:
| |
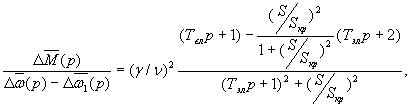 |
(41) |
где 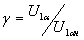 - относительное напряжение статора;
- относительное напряжение статора; 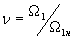 - относительная частота напряжения статора.
- относительная частота напряжения статора.
Или в упрощенном виде:
| |
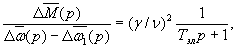 |
(42) |
Соответственно на основании уравнения (40) имеем
| |
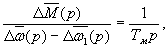 |
(43) |
где 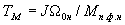 -механическая постоянная времени двигателя
Структурная схема асинхронного электродвигателя при управлении напряжением статора показана на рисунке 1.
-механическая постоянная времени двигателя
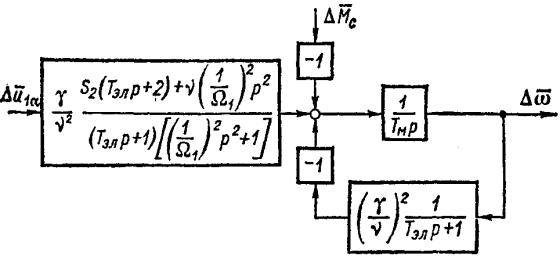
Структурная схема асинхронного электродвигателя при управлении напряжением статора показана на рисунке 1.
Рисунок 1. Структурная схема асинхронного двигателя при управлением напряжением статора.
При построении систем управления асинхронным электродвигателем часто оказывается целесообразным использовать информацию о токе статора или ротора. В связи с этим полную структурную схему асинхронного электродвигателя, объединяющую частные случаи управления, рассмотренные выше, целесообразно представить с выделенными приращениями токов 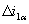 и
и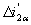 Такая структурная схема показана на рисунке 2. Дополнительно к ранее принятым обозначениям на рисунке 2 обозначено через
Такая структурная схема показана на рисунке 2. Дополнительно к ранее принятым обозначениям на рисунке 2 обозначено через 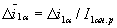 относительное приращение активного тока в обмотке статора, где
относительное приращение активного тока в обмотке статора, где 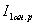 - активный ток в обмотке статора при номинальном напряжении, номинальной частоте и неподвижном роторе. С учетом принятых допущений справедливо приближенное равенство
- активный ток в обмотке статора при номинальном напряжении, номинальной частоте и неподвижном роторе. С учетом принятых допущений справедливо приближенное равенство
| |
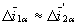 |
(44) |
где 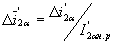 - относительное приращение активного тока ротора;
- относительное приращение активного тока ротора;
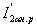 - активный ток в обмотке неподвижного ротора при номинальном напряжении и номинальной частоте напряжения статора.
- активный ток в обмотке неподвижного ротора при номинальном напряжении и номинальной частоте напряжения статора.
Рисунок 2. Полная структурная схема асинхронного электродвигателя
Для управления электродвигателями переменного тока используются различные тиристорные преобразователи (ТП): выпрямители и зависимые инверторы, автономные инверторы, преобразователи частоты, импульсные преобразователи, преобразователи напряжения. Схемы ТП весьма разнообразны и определяются конкретными требованиями к электроприводу переменного тока по таким показателям, как мощность, диапазон регулирования скорости, потери электроэнергии, простота реализации, форма выходного напряжения или тока и др.
Тиристорные преобразователи частоты, получившие наибольшее распространение в технике электропривода, разделяются на две большие группы: ТП частоты со звеном постоянного тока и частоты с непосредственной связью. В свою очередь ТП частоты со звеном постоянного тока разделяются на ТП частоты с управляемым или неуправляемым выпрямителем, с автономными инверторами тока или напряжения.
Рассматривая динамику двигателя переменного тока, работающего от преобразователя частоты, следует рассматривать электромагнитные процессы в двигателе с учетом электромагнитных процессов в инверторе. Наличие большого числа различных цепей в инверторе, переключающихся одновременно с переключением тиристоров, оказывает определенное влияние на формирование электромагнитного момента двигателя. Однако учет динамических процессов в периодически переключающихся электромагнитных цепях совместно с динамическими процессами в двигателе является сложным, и часто в этом не возникает необходимости в связи с ограниченным спектром формирования управляющих воздействий на преобразователь частоты в замкнутых системах управления.
При исследование динамики могут быть учтены в параметрах статорной цепи двигателя приведенные параметры АИ приводятся к параметрам якорной цепи электродвигателя. Наряду с этим в структуре ТП частоты имеется сглаживающий фильтр, существенно влияющий на динамику системы. В соответствии с эквивалентной схемой цепи выпрямитель-фильтр можно записать основные уравнения динамики такой цепи в приращениях координат относительно начальных значений:
| |
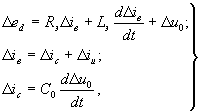 |
(45) |
где 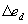 - приращение ЭДС выпрямителя;
- приращение ЭДС выпрямителя; 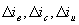 - приращение токов в цепях выпрямителя, конденсатора С0 и инвертора;
- приращение токов в цепях выпрямителя, конденсатора С0 и инвертора;
Переходя к операторной форме записи уравнений (45) и выполнив через коэффициенты ксг1 и ксг2 согласование переменных 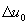 и
и 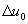 с переменными
с переменными 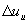 и
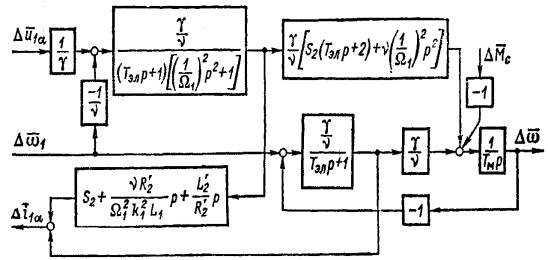
и 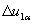 , которые раннее рассматривались при исследовании динамики в асинхронном электродвигателе, можно получить упрощенную структурную схему электромагнитной цепи ТП частоты, работающего на электродвигатель. В соответствии с этой структурной схемой и структурной схемой электродвигателя для случая одновременного пропорционального управления напряжением и частотой инвертора (рис. 2), а также предполагая отсутствие влияния на выходное напряжение инвертора и пренебрегая инерционностью электромагнитной цепи электродвигателя можно получить общую структурную схему электродвигателя совместно с преобразователем частоты (рис.3).
, которые раннее рассматривались при исследовании динамики в асинхронном электродвигателе, можно получить упрощенную структурную схему электромагнитной цепи ТП частоты, работающего на электродвигатель. В соответствии с этой структурной схемой и структурной схемой электродвигателя для случая одновременного пропорционального управления напряжением и частотой инвертора (рис. 2), а также предполагая отсутствие влияния на выходное напряжение инвертора и пренебрегая инерционностью электромагнитной цепи электродвигателя можно получить общую структурную схему электродвигателя совместно с преобразователем частоты (рис.3).
Рисунок 3. Общая структурная схема электродвигателя совместно с преобразователем частоты.
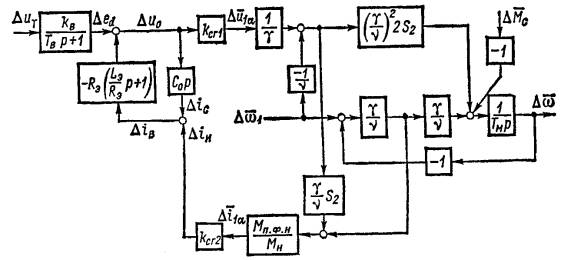
Динамические свойства выпрямителя по управляющему воздействию учтены инерционным звеном 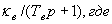 кв Тв – передаточный коэффициент и постоянная времени выпрямителя.
кв Тв – передаточный коэффициент и постоянная времени выпрямителя.
Далее будут представлены анимированные графические изображения прямого пуска асинхронного электропривода, и частотно-управляемый пуск асинхронного электропривода согласно структурным схемам приведенным выше.
Рисунок 4. Анимированное изображение прямого пуска асинхронного электропривода. (для просмотра изображения нажать кнопку  "обновить" на панели инстументов).
"обновить" на панели инстументов).
Рисунок 5. Анимированное изображение частотно-управляемого пуска асинхронного электропривода. (для просмотра изображения нажать кнопку  "обновить" на панели инстументов).
"обновить" на панели инстументов).
Как видно из графических зависимостей представленных на рисунках 5,6 при различных законах регулирования получаются различные значения момента, токов, и частоты вращения. Прямой пуск характерен: токами в статарной обмотке достигающими 5-6 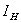 . Переменные и постоянные потери вызывают интенсивное нагревание двигателя, в первую очередь обмоток статора. Электромагнитный момент достигает 6
. Переменные и постоянные потери вызывают интенсивное нагревание двигателя, в первую очередь обмоток статора. Электромагнитный момент достигает 6 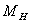 при пуске, влияет на обмотки статора и механическую передачу. Время действия этих моментов относительно невелико, но все же это способствует накоплению деформаций, уменьшению ресурса системы.
при пуске, влияет на обмотки статора и механическую передачу. Время действия этих моментов относительно невелико, но все же это способствует накоплению деформаций, уменьшению ресурса системы.
Если же применять частотное регулирование асинхронного электропривода, то сразу становится видно, насколько уменьшились пусковые моменты и токи. А все это способствует уменьшению потерь, а значит и повышению КПД и 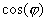 . Так что дальнейшая работа по моделированию асинхронных частотно-регулируемых приводов должна сводится к разработке такой модели регулирования
. Так что дальнейшая работа по моделированию асинхронных частотно-регулируемых приводов должна сводится к разработке такой модели регулирования 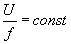 , которая бы позволила максимально образам увеличить КПД электропривода,
, которая бы позволила максимально образам увеличить КПД электропривода, 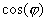 двигателя, и КПД всего очистного комбайна в целом.
двигателя, и КПД всего очистного комбайна в целом.
А что касаемо того, какой показатель важнее КПД или 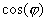 , по этому поводу можно сказать следующее – эти два коэффициента не равноценны. Желание повысить
, по этому поводу можно сказать следующее – эти два коэффициента не равноценны. Желание повысить 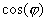 безусловно прогрессивное, потому что разгружается система от реактивных токов. Оно дает позитивные результаты, если повышение
безусловно прогрессивное, потому что разгружается система от реактивных токов. Оно дает позитивные результаты, если повышение 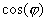 осуществляется не за счет снижения КПД.
осуществляется не за счет снижения КПД.
Каждый процент повышения КПД, в десятки раз рентабельней, нежели процент повышения коэффициента мощности. Так как для производства одного киловатта активной мощности необходимо затратить 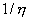 кВт мощности, то есть при
кВт мощности, то есть при 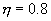 необходимо затратить 1/0,8 = 1,25 кВт. В то же время для производства реактивной мощности необходимо затратить всего 0,02 – 0,08 киловатта.
необходимо затратить 1/0,8 = 1,25 кВт. В то же время для производства реактивной мощности необходимо затратить всего 0,02 – 0,08 киловатта.
Так что главным энергетическим показателем нужно считать КПД и добиваться его максимально возможных значений.
В перечень нерешенных проблем и вопросов входят:
- не до конца разработана модель в пакете Matlab,
- не рассчитана стоимость разработки и внедрения такого устройства, и экономическая выгода от его эксплуатации,
- не рассчитаны массогабаритные показатели.
Планируемым результатом по данной теме является полная разработка математической модели этого устройства, с проверкой ее адекватности в пакете Matlab. Разработка технических решений касаемых внедрения комплектующих в это устройство (IGBT – транзисторы, микроконтроллер и прочее “железо”).
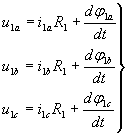
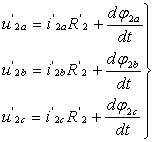
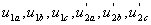 - мгновенные значения фазных напряжений статора и ротора;
- мгновенные значения фазных напряжений статора и ротора;
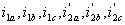 -мгновенные значения фазных токов статора и ротора;
-мгновенные значения фазных токов статора и ротора;
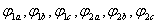 - полные потокосцепления фазных обмоток;
- полные потокосцепления фазных обмоток;
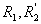 - активные сопротивления обмоток статора и ротора.
- активные сопротивления обмоток статора и ротора.
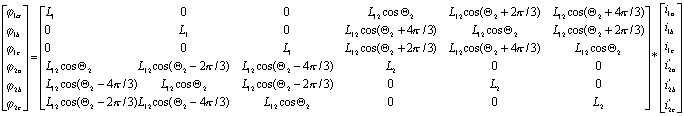
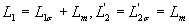 - полные эквивалентные индуктивности фаз статора и ротора, состоящие из индуктивностей от полей рассеяния
- полные эквивалентные индуктивности фаз статора и ротора, состоящие из индуктивностей от полей рассеяния 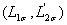 и главного потока
и главного потока 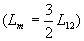 ; L12 — максимальная взаимная индуктивность между любой обмоткой статора и любой обмоткой ротора, которая имеет место при совпадении их осей;Q2 — текущий угол между осями обмоток фаз ротора и статора.
; L12 — максимальная взаимная индуктивность между любой обмоткой статора и любой обмоткой ротора, которая имеет место при совпадении их осей;Q2 — текущий угол между осями обмоток фаз ротора и статора.
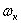 Такое преобразование координат соответствует приведению трехфазного электродвигателя к эквивалентному двухфазному.
Такое преобразование координат соответствует приведению трехфазного электродвигателя к эквивалентному двухфазному.
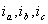 то результирующий вектор тока определяется уравнением:
то результирующий вектор тока определяется уравнением:
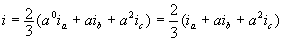
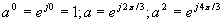
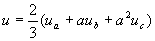
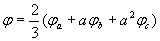
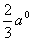 , второе на
, второе на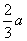 третье на
третье на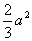 .Суммируя полученные произведения, получим
.Суммируя полученные произведения, получим
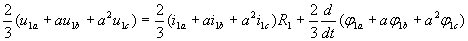
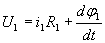
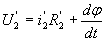
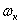 имеют вид
имеют вид
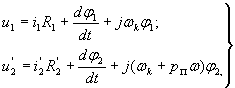
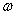 - угловая скорость вращения ротора; рп – число пар полюсов.
- угловая скорость вращения ротора; рп – число пар полюсов.
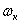 , равной угловой скорости вращения магнитного поля
, равной угловой скорости вращения магнитного поля 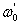 , приведенной к числу пар полюсов, равному единице (приведенной к двухполюсному электродвигателю).
, приведенной к числу пар полюсов, равному единице (приведенной к двухполюсному электродвигателю).
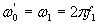
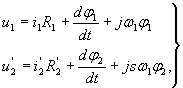
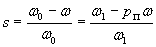 ,(
,( 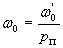 - угловая скорость вращения магнитного поля, или синхронная скорость электродвигателя).
- угловая скорость вращения магнитного поля, или синхронная скорость электродвигателя).
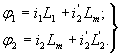
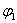 и
и 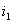 ,тогда
,тогда
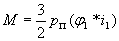
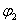 и
и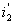 , тогда
, тогда
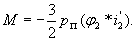
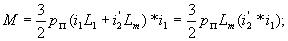
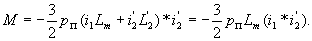
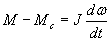
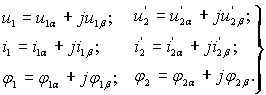
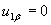 на основании (7) получим
на основании (7) получим
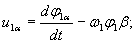
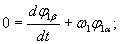
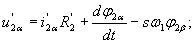
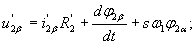
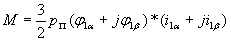 и применив правило векторного произведения векторов, получим абсолютное значение момента:
и применив правило векторного произведения векторов, получим абсолютное значение момента:
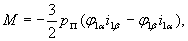
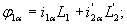 ,
,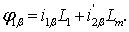
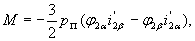
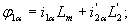 ,
,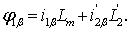
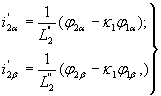
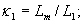
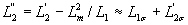
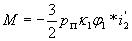 или
или
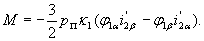
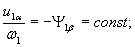 ,
, 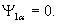
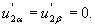 Выразив из уравнении (20)
Выразив из уравнении (20) 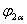 и
и 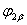 и подставив их в уравнения (17), (18), получим
и подставив их в уравнения (17), (18), получим
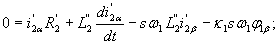
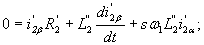
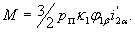
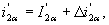 ,
,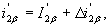 ,
,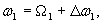 ,
,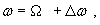 ,
,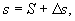 ,
,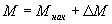 ,получим из (23) – (26) уравнения для статического режима, связывающие начальные значения координат,
,получим из (23) – (26) уравнения для статического режима, связывающие начальные значения координат,
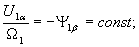
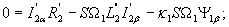
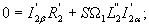
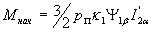
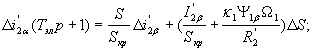
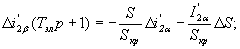
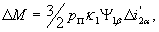
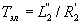 - электромагнитная постоянная электродвигателя;
- электромагнитная постоянная электродвигателя;
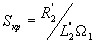 - критическое скольжение.
- критическое скольжение.
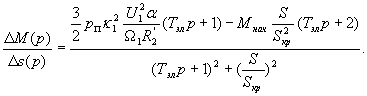
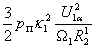 в первом слагаемом числителя (34) представляет собой значение фиктивного пускового момента Мп.ф., определяемое в результате линеаризации рабочей части механической характеристики двигателя для принятых значений напряжения статора
в первом слагаемом числителя (34) представляет собой значение фиктивного пускового момента Мп.ф., определяемое в результате линеаризации рабочей части механической характеристики двигателя для принятых значений напряжения статора 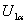 и угловой частоты напряжения статора
и угловой частоты напряжения статора 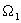 :
:
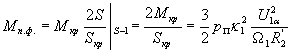
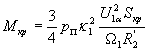 - критический момент двигателя.
- критический момент двигателя.
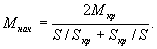
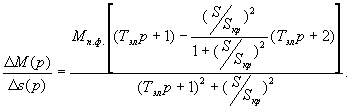
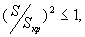 и тогда передаточную функцию (37) можно записать в упрощенном виде
и тогда передаточную функцию (37) можно записать в упрощенном виде
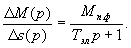
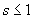 , получим
, получим
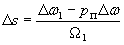
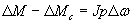
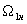 ,
,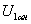 ,
,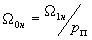 ,где
,где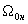 - синхронная угловая скорость двигателя. Тогда
- синхронная угловая скорость двигателя. Тогда
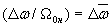 ,
,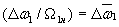 ,
,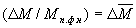 ,
,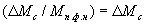 ,
,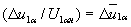 .Передаточная функция (37) с учетом (39) запишется так:
.Передаточная функция (37) с учетом (39) запишется так:
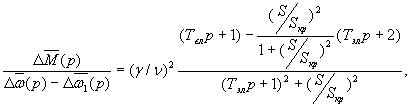
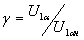 - относительное напряжение статора;
- относительное напряжение статора; 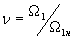 - относительная частота напряжения статора.
- относительная частота напряжения статора.
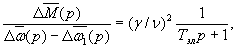
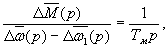
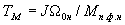 -механическая постоянная времени двигателя
Структурная схема асинхронного электродвигателя при управлении напряжением статора показана на рисунке 1.
-механическая постоянная времени двигателя
Структурная схема асинхронного электродвигателя при управлении напряжением статора показана на рисунке 1.
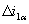 и
и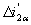 Такая структурная схема показана на рисунке 2. Дополнительно к ранее принятым обозначениям на рисунке 2 обозначено через
Такая структурная схема показана на рисунке 2. Дополнительно к ранее принятым обозначениям на рисунке 2 обозначено через 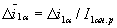 относительное приращение активного тока в обмотке статора, где
относительное приращение активного тока в обмотке статора, где 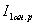 - активный ток в обмотке статора при номинальном напряжении, номинальной частоте и неподвижном роторе. С учетом принятых допущений справедливо приближенное равенство
- активный ток в обмотке статора при номинальном напряжении, номинальной частоте и неподвижном роторе. С учетом принятых допущений справедливо приближенное равенство
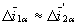
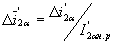 - относительное приращение активного тока ротора;
- относительное приращение активного тока ротора;
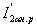 - активный ток в обмотке неподвижного ротора при номинальном напряжении и номинальной частоте напряжения статора.
- активный ток в обмотке неподвижного ротора при номинальном напряжении и номинальной частоте напряжения статора.
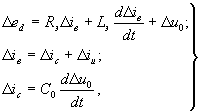
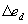 - приращение ЭДС выпрямителя;
- приращение ЭДС выпрямителя; 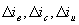 - приращение токов в цепях выпрямителя, конденсатора С0 и инвертора;
- приращение токов в цепях выпрямителя, конденсатора С0 и инвертора;
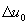 и
и 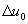 с переменными
с переменными 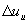 и
и 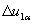 , которые раннее рассматривались при исследовании динамики в асинхронном электродвигателе, можно получить упрощенную структурную схему электромагнитной цепи ТП частоты, работающего на электродвигатель. В соответствии с этой структурной схемой и структурной схемой электродвигателя для случая одновременного пропорционального управления напряжением и частотой инвертора (рис. 2), а также предполагая отсутствие влияния на выходное напряжение инвертора и пренебрегая инерционностью электромагнитной цепи электродвигателя можно получить общую структурную схему электродвигателя совместно с преобразователем частоты (рис.3).
, которые раннее рассматривались при исследовании динамики в асинхронном электродвигателе, можно получить упрощенную структурную схему электромагнитной цепи ТП частоты, работающего на электродвигатель. В соответствии с этой структурной схемой и структурной схемой электродвигателя для случая одновременного пропорционального управления напряжением и частотой инвертора (рис. 2), а также предполагая отсутствие влияния на выходное напряжение инвертора и пренебрегая инерционностью электромагнитной цепи электродвигателя можно получить общую структурную схему электродвигателя совместно с преобразователем частоты (рис.3).
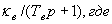 кв Тв – передаточный коэффициент и постоянная времени выпрямителя.
кв Тв – передаточный коэффициент и постоянная времени выпрямителя.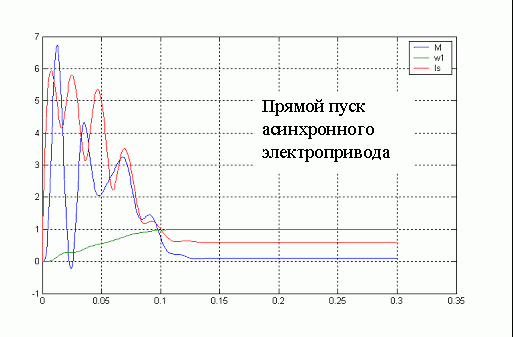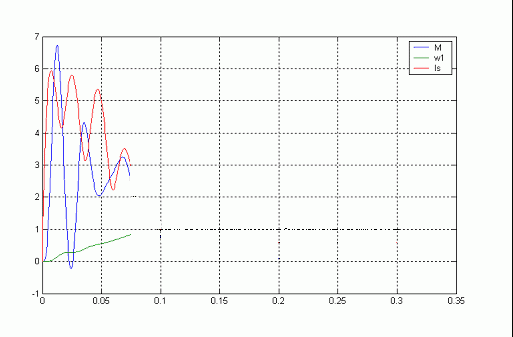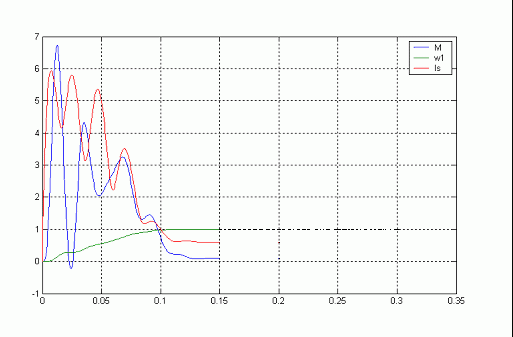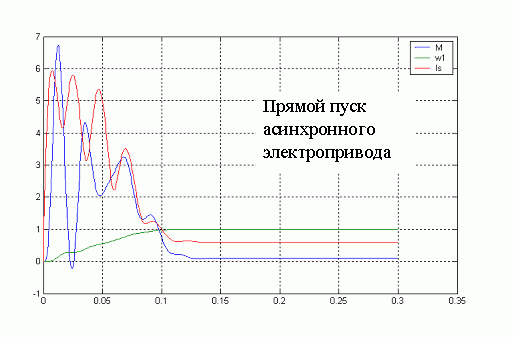
 "обновить" на панели инстументов).
"обновить" на панели инстументов).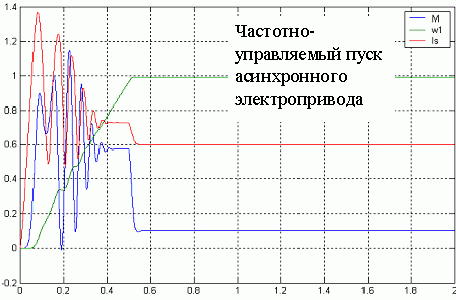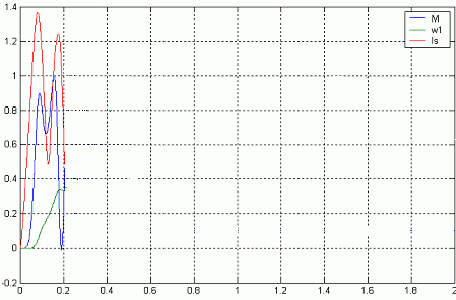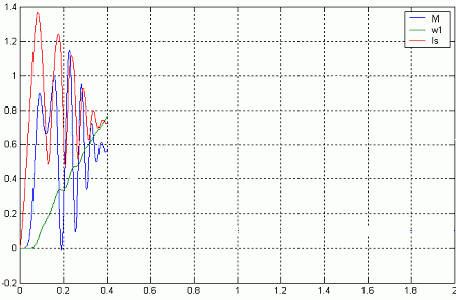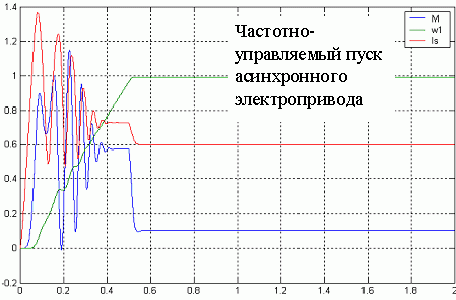
 "обновить" на панели инстументов).
"обновить" на панели инстументов).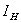 . Переменные и постоянные потери вызывают интенсивное нагревание двигателя, в первую очередь обмоток статора. Электромагнитный момент достигает 6
. Переменные и постоянные потери вызывают интенсивное нагревание двигателя, в первую очередь обмоток статора. Электромагнитный момент достигает 6 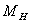 при пуске, влияет на обмотки статора и механическую передачу. Время действия этих моментов относительно невелико, но все же это способствует накоплению деформаций, уменьшению ресурса системы.
при пуске, влияет на обмотки статора и механическую передачу. Время действия этих моментов относительно невелико, но все же это способствует накоплению деформаций, уменьшению ресурса системы.
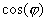 . Так что дальнейшая работа по моделированию асинхронных частотно-регулируемых приводов должна сводится к разработке такой модели регулирования
. Так что дальнейшая работа по моделированию асинхронных частотно-регулируемых приводов должна сводится к разработке такой модели регулирования 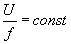 , которая бы позволила максимально образам увеличить КПД электропривода,
, которая бы позволила максимально образам увеличить КПД электропривода, 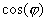 двигателя, и КПД всего очистного комбайна в целом.
двигателя, и КПД всего очистного комбайна в целом.
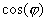 , по этому поводу можно сказать следующее – эти два коэффициента не равноценны. Желание повысить
, по этому поводу можно сказать следующее – эти два коэффициента не равноценны. Желание повысить 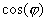 безусловно прогрессивное, потому что разгружается система от реактивных токов. Оно дает позитивные результаты, если повышение
безусловно прогрессивное, потому что разгружается система от реактивных токов. Оно дает позитивные результаты, если повышение 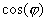 осуществляется не за счет снижения КПД.
осуществляется не за счет снижения КПД.
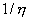 кВт мощности, то есть при
кВт мощности, то есть при 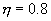 необходимо затратить 1/0,8 = 1,25 кВт. В то же время для производства реактивной мощности необходимо затратить всего 0,02 – 0,08 киловатта.
необходимо затратить 1/0,8 = 1,25 кВт. В то же время для производства реактивной мощности необходимо затратить всего 0,02 – 0,08 киловатта.