Автореферат магистерской диссертации

на тему: “Исследование обменных процессов при помощи численных экспериментов с целью модернизации тепловых агрегатов”

Наука расширяет границы познания согласно принципу: “A potentia ad actum” – “От возможного к действительному”. В связи с этим перед современным исследователем встают все более сложные задачи, получение решений для которых методами классического математического анализа невозможно.

Формулируемая математическая модель практически любой задачи характеризуется системой взаимосвязанных дифференциальных уравнений с частными производными, аналитическое решение которой невозможно. Это объясняется сложной геометрией исследуемых объектов; одновременным протеканием и взаимным влиянием таких процессов как: гидродинамические ламинарные и турбулентные течения, различные виды тепломассообмена, электрические и магнитные явления; неединственным решением дифференциальных уравнений в частных производных и т. д.

Все перечисленные выше процессы в той или иной комбинации происходят в тепловых агрегатах (промышленных печах, котельных установках, ТВЭЛах ядерных реакторов, МГД генераторах и т.д.).

Таким образом, зачастую единственным средством для нахождения решения практически важных задач являются численные методы. Пионерами в области вычислительных технологий являются такие науки как: вычислительная гидродинамика и теплообмен, которые являются базовыми для реализации математического моделирования процессов переноса в технических агрегатах и явлениях природы.

Цель магистерской диссертации – получить решение системы дифференциальных уравнений, описывающих конвективный теплообмен и диффузионные процессы в теплоэнергетическом агрегате (парогенераторе) в двухмерной декартовой системе координат при помощи проведения численного эксперимента. Также в работе планируется определить локальное изменение коэффициента теплоотдачи α на всех поверхностях теплового агрегата.

Математическая модель задачи состоит из следующей системы уравнений.

Уравнение движения в проекции на ось X:

Уравнение движения в проекции на ось Y (с учетом массовой силы или силы тяжести):

,

где – компоненты тензора вязких напряжений:

Уравнение неразрывности:

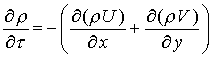
Уравнение теплопроводности в подвижных средах (уравнение Фурье – Кирхгофа):

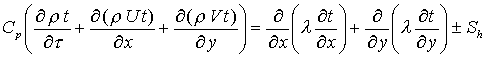
Уравнение теплопроводности (уравнение Фурье) для твердых тел:

Уравнение связи:

При исследовании процессов горения данная система дополняется еще тремя уравнениями массопереноса. Если предположить, что между горючим и окислителем протекает необратимая одностадийная экзотермическая химическая реакция:

,

где Г – горючее; О – окислитель; ПГ – продукты горения; ν_i – стехиометрические коэффициенты, то для исследуемой области уравнения диффузии для горючего и окислителя будут иметь вид:

,

где C_г = ρ_г / ρ – относительная массовая концентрация горючего; C_ок = ρ_ок / ρ – относительная массовая концентрация окислителя; m_г и m_ок – скорости расходования горючего и окислителя только в одной химической реакции. Для продуктов горения можно записать – C_пг = ρ_пг / ρ.

Таким образом, сумма всех относительных массовых концентраций равна единице. Следовательно, относительная массовая концентрация продуктов горения определяется из уравнения:

Приведенная система уравнений дополняется условиями однозначности, которые включают в себя:

• Геометрические условия, которые определяют форму и размеры области, в которой протекает исследуемый процесс;

• Физические условия задаются теплофизическими свойствами вещества, которое заполняет исследуемую область. Кроме того, они учитывают распределение внутренних источников и стоков теплоты по объему;

• Временные (начальные) условия содержат распределение искомой величины в исследуемой области в начальный момент времени;

• Граничные условия, которые определяют особенности протекания процесса на границах исследуемой области.

Решение первых трех уравнений (расчет поля течения) предполагается получить при помощи метода SIMPLER. Нахождение решений уравнений теплопроводности в подвижных средах и твердых телах, а также уравнений диффузии для горючего и окислителя осуществляется по известным полям составляющих скорости U, V при помощи программы CONDUCT.

Решение поставленной задачи численными методами даст распределение составляющих скорости U и V, давления, температуры, концентраций: C_г, C_ок, C_пг во всей исследуемой области теплового агрегата.