Е.Н. Смирнов, В.А. Скляр, А.П. Митьев, О.С. Киливник, И.А. Яценко, А.И. Горбенко, А.В. Оболянская
Представлены результаты первого этапа исследований с помощью физических моделей процесса «мягкого» обжатия непрерывнолитых блюмов. Показано, что разработанный метод моделирования позволяет повысить степень подобия между физической моделью и натуральным объектом, а также предоставляет необходимый объем первичной экспериментальной информации для исследования напряженно-деформированного состояния
ВВЕДЕНИЕ. Повышение требований к качеству непрерывнолитой заготовки стимулировало развитие принципов «мягкого» обжатия с целью подавления осевой пористости и ликвации.
В тоже время, дальнейшее совершенствование системы технологического проектирования метода «мягкого» обжатия непрерывнолитых блюмов и заготовок требует, в свою очередь, создания новых устройств и технологий для реализации процесса. При этом, учитывая высокую степень наукоемкости рассматриваемой технологии, проведение дальнейших исследований целесообразно осуществлять в двух направлениях:
- создание математических моделей процесса «мягкого» обжатия;
- исследование процесса «мягкого» обжатия на физических моделях.
Моделирование процесса «мягкого» обжатия с использованием физических моделей сопряжено с применением комплексного подхода, основанного на положениях теории конечных деформаций и закономерностях теории теплообмена.
Так, в работе [1] в ходе физического моделирования на пластилиновых образцах, исследовалась динамика сближения фронтов кристаллизации при обжатии моделирующего образца. Определялась доля пластической и упругой составляющей деформации без учета наличия перепада температуры по сечению образца. В тоже время, как было показано в работе [2], перепад температуры оказывает существенное влияние на формируемое напряженно-деформированное состояние слитка.
Не в полной мере разработаны методики, касающиеся прогнозирования качества получаемого полупродукта.
Учитывая вышеизложенное, целью данного исследования являлась разработка усовершенствованного метода получения экспериментальной информации на основе физического моделирования процесса «мягкого» обжатия и исследование формируемого напряженно-деформированного состояния в наиболее дефектоопасных местах.
ОБЪЕКТ И УСЛОВИЯ МОДЕЛИРОВАНИЯ. Как объект для моделирования был выбран непрерывнолитой блюм сечением 335x400 мм, который отливается в условиях блюмовой МНЛЗ ОАО «Днепровский металлургический комбинат им. Ф.Э. Дзержинского».
На первом этапе с помощью математического моделирования исследовалось тепловое состояние непрерывнолитого блюма в процессе разливки [2,3,4]. Результатом выполненного моделирования стали геометрические модели поперечного сечения непрерывнолитого блюма для определенного времени кристаллизации, построенные на основе изучения перемещения границы фазового перехода «расплав – твердокристаллическое состояние».
В качестве факторов эксперимента использовали следующие независимые величины: Dh/H0 - отношение абсолютного обжатия к начальной высоте образца, F0/F – отношение площади отверстия, имитирующего жидко-твердую фазу, к площади поперечного сечения образца и q=(Тпл-Т)/Тпл - отношение разницы температуры плавления Тпл и температуры наружной поверхности образца Т к температуре плавления.
План эксперимента приведен в табл. 1.
Таблица 1.Уровни и интервалы варьирования параметров
|
Параметры |
Интервал варьирования |
Основной уровень (0) |
Верхний уровень (+1) |
Нижний уровень (-1) |
|
Dh/H0 |
0,03 |
0,06 |
0,09 |
0,03 |
|
F0/F |
0,016 |
0,098 |
0,114 |
0,054 |
|
q=(Тпл-Т)/Тпл |
0,057 |
0,323 |
0,318 |
0,266 |
Для проведения экспериментальных исследований изготавливались в масштабе 1:10 пустотелые пластилиновые образцы. Размер отверстия, моделирующего жидкую фазу, отвечал металлургической длине слитка 13, 15 и 17 м. Для изучения процесса деформации, на боковую и контактную поверхность образца наносилась координатная сетка в виде окружностей (рис. 1).

Рис. 1 – Внешний вид образца с нанесенной координатной сеткой
Принципиальным моментом для исследуемого процесса является вопрос обеспечения подобия распределения температур по сечению в натуральном непрерывнолитом слитке и физической модели. Именно данная составляющая разработанной комбинированной методики физического моделирования является наиболее сложной и требует детального изучения. Для обеспечения подобия распределения температур по сечению непрерывнолитого блюма был разработан новый способ моделирования [5], включающий в себя одновременный нагрев внутренней полости и охлаждение наружных граней. Для проведения экспериментальных исследований была разработана установка, позволяющая приблизится к натурным условиям в части достижения подобия распределения температуры по сечению раската. Схема установки приведена на рис. 2. В ходе выполнения эксперимента образец 7 помещался в калориметр 3 на специальную подставку 5. В дальнейшем, внутрь образца помещался трубчатый электронагревательный элемент 2, закрепленный на штативе 1, а полость образца заполнялась маслом 6. Для внешнего охлаждения образца использовалась смесь этилового спирта с углекислым газом. Температура смеси определялась на основании расчета гомологической температуры моделирующего материала по методике изложенной в работе [6]. Контроль над температурой осуществлялся при помощи термопар 8, помещенных в различные точки и фиксировался через коммутационный блок 9 при помощи осциллографа 10.

Рис. 2 – Схема экспериментальной установки
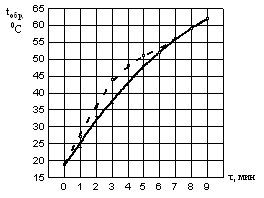
Первичные эксперименты показали, что использование стенда в вышеописанном виде не позволяет обеспечить одинаковую температуру по высоте образца. Верхняя часть образца имела более высокую температуру, чем нижняя. Данное обстоятельство приводило к росту погрешности эксперимента. Для стабилизации температурного состояния по высоте моделирующего образца было предложено осуществлять продувку теплоносителя (масла) потоком воздуха подаваемого при помощи насоса 11. Внедрение такого подхода позволило с одной стороны, стабилизировать температурное состояние по высоте образца (рис. 3), а с другой – добиться физического подобия в части оплавления границы «теплоноситель – моделирующий материал» (рис. 4).
 а)
а)
 б)
б)
Рис.3 - Динамика изменения температуры в различных точках физической модели без наличия продувки (а) и с продувкой (б)
Полученные зависимости динамики изменения температуры по сечению физических моделей были обработаны по первоначально разработанной программе расчета температурного состояния кристаллизирующегося блюма[4].
В результате выполненного математического моделирования была детализирована зависимость коэффициента теплоотдачи a от температуры хладагента для пластилиновых физических моделей, которая приведена на рис. 5. Последующие расчеты при помощи разработанной математической модели теплового состояния непрерывнолитого блюма для условий предложенной физической модели позволили определить необходимые температурно-временные параметры процесса «охлаждения-нагрева». В ходе математического моделирования температуру хладагента принимали равной гомологической температуре поверхностных слоев пластилина, соответствующих температуре поверхности слитка 1000, 900, и 800 °С.

Рис. 4 – Внешний вид внутренней полости физической модели после нагрева образца.
В дальнейшем образцы с заданным температурным градиентом прокатывались на лабораторном стане с получением недокатов. Деформированная координатная сетка фиксировалась при помощи цифрового фотоаппарата.
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.Полученное изображение недокатов (рис. 6) обрабатывали в программе AutoCAD, в результате чего получали исходный массив координат Х и У деформированной координатной сетки. Последующая обработка массива координат производилась в соответствии с методикой изложенной в работе [7] и ранее апробированной в условиях деформации высоких полос.

Рис. 6 - Внешний вид пластилиновой физической модели с деформированной координатной сеткой после прокатки
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА. В результате обработки данных эксперимента получено представление о распределении деформации в непрерывнолитом слитке при реализации процесса «мягкого» обжатия (рис. 7).

Рис. 7 – Распределение относительного обжатия по длине очага деформации
Как видно из графика, в большей степени деформируются приконтактные и промежуточные слои, а в центральные области деформация проникает незначительно и с некоторым отставанием. Кроме того, приконтактный слой деформируется по высоте в меньшей степени, чем промежуточный. Это объясняется, по всей видимости, особенностями деформирования особо высоких полос, к которым в полной мере может быть отнесен и рассматриваемый процесс. Когда приконтактный слой полностью находиться в зоне прилипания, распространяющейся почти на всю длину очага деформации. Вследствие этого, преобладает течение металла в поперечном направлении[8].
После выхода из геометрического очага деформации наблюдается частичное восстановление первоначальных размеров слитка. Данный эффект связан с наличием упругой составляющей, которая проявляется при относительно малых степенях деформации, являющихся характерными для условий реализации процесса «мягкого» обжатия[1]. Распределение продольной деформации имеет похожий характер.

Рис. 8 - Кривые распределения L и Y по высоте закристаллизовавшейся части непрерывнолитого блюма.
Сопоставление полученных зависимостей с данными исследований по прокатке высоких полос[7] позволяют говорить об адекватности полученных данных существующим положениям теории обработки металлов давлением и о возможности использования предложенного метода моделирования для исследования напряженно-деформированного состояния в непрерывнолитых блюмах с жидкой сердцевиной при реализации технологии «мягкого» обжатия.
Выводы Представлены результаты экспериментальной проверки применимости нового метода физического моделирования процесса «мягкого» обжатия непрерывнолитых блюмов для исследования напряженно-деформированного состояния на контактной и боковых гранях. В ходе лабораторных экспериментов отработана методика проведения опытов обеспечивающая максимальное тепловое подобие, а также показана принципиальная возможность использования предложенного подхода для определения показателей накопленной степени деформации L и ресурса пластичности Y в различных точках поверхности раската.
ЛИТЕРАТУРА
1. Смирнов Е.Н., Григорьев М.В. Исследование влияния деформационных параметров «мягкого» обжатия на сближение фронтов кристаллизации с использованием физических моделей // Ресурсозберігаючі технології виробництва та обробки тиском матеріалів у машинобудуванні: Зб. наук. пр. – Луганськ: вид-во СНУ ім. В.Даля, 2004, т.2. –С. 93-99.
2. Смирнов Е.Н. Скляр В.А. Моделирование двухстадийного процесса «мягкого» обжатия непрерывнолитых блюмов // Удосконалення процесів і обладнання обробки тиском в металургії і машинобудуванні, Тематич. сб.наук.пр.: ДДМА, Краматорськ, 2005. – с.441-445
3. Минаев А.А., Смирнов Е.Н., Григорьев. М.В. Моделирование теплового состояния непрерывнолитого блюма в процессе вторичного охлаждения // Металл и литьё Украины. -№6. –2003. –С.18-22.
4. Теоретический CAD/CAE анализ теплового состояние непрерывнолитого блюма в зоне «мягкого» обжатия / Е.Н. Смирнов, М.В. Григорьев, В.В. Передереев, В. Скляр // Удосканалення процесів і обладнання обробки тиском в металургії і машинобудуванні: Тематич. зб. наук. пр. – ДДМА. Краматорськ. -2004. - 656 с.
5. Заявка № 20040705491 от 07.07.04. Спосіб фізичного моделювання процесів деформування безперервнолитих зливків у рідко-твердому стані / Е.М. Смирнов та ін.
6. А.с. №868451 СССР, МКИ G 01 N 3/28. Способ моделирования горячего пластического формоизменения металлов и сплавов /В.В. Лашин, В.К. Воронцов, А.В. Бринза(СССР). – N 2870405; Заявлено 10.01.80.
7. Пилюшенко А.В, Смирнов Е.Н., Белевитин В.А. Математическая модель показателей напряженного состояния на боковой грани при прокатке высоких поло. Удосконалення процесів і обладнання обробки тиском в металургії і машинобудуванні, Тематич. сб.наук.пр.: ДДМА, Краматорськ-2005. – с.441-445.