Р [n]=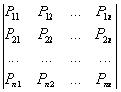 
(2)
Pi/i+1 = f (Si , S i-1, S i-2) (1)
1. Имеется совокупность переходных вероятностей в виде матрицы:
Р [n]= 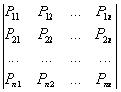(2)
2. Вектор начальных вероятностей описывающий начальное состояние системы.
P(0)- в случае невозвратного множества возможны любые переходы внутри этого множества. Система может покинуть это множество, но не может вернуться в него.
- в случае возвратного множества также возможны любые переходы внутри множества. Система может войти в это множество, но не может покинуть его.
- в случае эргодического множества возможны любые переходы внутри множества, но исключены переходы из множества и в него.
- при попадании системы в поглощающее множество процесс заканчивается.
Кроме описанной выше классификации множеств различают состояния системы:
а) существенное состояние - возможны переходы из Si в Sj и обратно
б) несущественное состояние - возможен переход из Si в Sj, но невозможен обратный.
В некоторых случаях, несмотря на случайность процесса, имеется возможность до определенной степени управлять законами распределения или параметрами переходных вероятностей. Такие марковские цепи называются управляемыми. Очевидно, что с помощью управляемых цепей Маркова (УЦМ) особенно эффективным становится процесс принятия решений. Как указывалось выше, основным признаком ДМЦ является детерминированность временных интервалов между отдельными шагами (этапами) процесса. Однако, часто в реальных процессах это свойство не соблюдается и интервалы оказываются случайными с каким-либо законом распределения, хотя марковость процесса сохраняется. Такие случайные последовательности называются полумарковскими. Кроме того, с учетом наличия и отсутствия тех или иных, упомянутых выше, множеств состояний, марковские цепи могут быть поглощающими, если имеется хотя бы одно поглощающее состояние, или эргодическими, если переходные вероятности образуют эргодическое множество. В свою очередь, эргодические цепи могут быть регулярными или циклическими. Циклические цепи отличаются от регулярных тем, что в процессе переходов через определенное количество шагов (цикл) происходит возврат в какое-либо состояние. Регулярные цепи этим свойством не обладают.- использование рекламы - стратегия 1;
- проведение дополнительных исследований требований потребителя и своих возможностей - стратегия 2.
Предположим также, что при попадании в то или иное состояние возможно объединение этих стратегий, то есть:- в состоянии S1 - реклама не используется и исследования не проводятся (стратегия 1);
- в состоянии S2 - используются и реклама и дополнительные исследования (стратегия 2).
Очевидно, что переходы из состояния в состояние образуют случайную последовательность, обладающую свойством последействия. Кроме того, здесь нет поглощающих состояний и возможны любые переходы, то есть ДМЦ - обладает свойством эргодичности. Допустим также, что в результате предварительного опыта известны переходные вероятности такой цепи, а также значения доходов (расходов), связанные с применением той или иной стратегии, а также вероятностями успешного или неуспешного выпуска продукции. Все сведения представлены в таблице 2.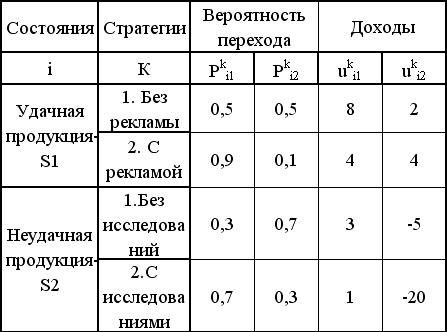
где qi - непосредственно ожидаемый доход; vi (n-1) - полный средний ожидаемый доход в течение остав- шихся n-1- этапов процесса. Для стратегии 1 (к = 1):
q(1)1 = 0,5 Ч 8 + 0,5 Ч 2 = 5; q(1)2 = 0,3 Ч 3 + 0,7 Ч (-5) = - 2,6.
При подсчете величины vi (n - 1) удобнее начинать с конца процесса, так как при снятии продукции vi(0) = v2(0) = 0. Тогда за один квартал (шаг) до конца процессаv(1)1(1) = q(1)1 = 5; v2(1) = q(1)2 = -2,6.
Для определения полного ожидаемого дохода за два квартала (шага) до смены продукции надо учесть, что система может оказаться в одном из двух состояний. При этом величины ожидаемых доходов vi (n - 1) определяются с учетом переходных вероятностей:v(1)1(2) = 0,5 Ч 5 + 0,5 Ч (-2,6) = 1,2 v(1)2(2) = 0,3 Ч 5 + 0,7 Ч (-2,6) = -0,32
Тогда полный суммарный доход за два квартала при первой стратегии будет равен:v(1)1S (2) = 5 + 1,2 = 6,2; v(1)2S (2) = -2,6 - 0,32 = -2,92.
Соответственно, доход за три квартала подсчитывается аналогично:v(1)1(3) = 0,5 Ч 6,2 + 0,5 Ч (-2,92) = 1,64 v(1)1(3) = 0,3 Ч 6,2 + 0,7 Ч (-2,92) = -0,184
Полный доход будет равен:v(1)1S (3) = 5 + 1,64 = 6,64; v(1)1S (3) = -2,6 +(-0,184) = -2,784.
Окончательный доход при первой стратегии будет равен:v(1)1(4) = 0,5Ч 6,64 + 0,5 Ч (-2,784) = 1,928. v(1)2(4) = 0,3 Ч 6,64 + 0,7 Ч (-2,784) = -0,044.
Тогда полный окончательный доход будет равен:v(1)1S (4) = 5 + 1,928 = 6,928; v(1)2S (4) = -2,6 + (-0,044) = -2,644.
Аналогичные расчеты должны быть теперь проделаны при второй стратегии. Можно сделать следующие выводы:- оптимальная стратегия на каждом шаге должна выбираться по максимальному значению помимо дохода. Оптимальность стратегии на всем многошаговом процессе обеспечивается применением принципа оптимальности Беллмана, согласно которому оптимальное управление в многошаговом процессе должно быть оптимальным на каждом шаге с учетом пред истории процесса; - в данном случае на основании расчетов при начале процесса из состояния S1 , вектор оптимальных стратегий будет иметь вид: f1 = < 2, 2, 2, 1> , а если начальным было состояние S2 , то f2 = < 2, 2, 1, 1> .
Это означает, что, если фабрика начала выпускать сразу удачную модель, то первые три квартала выгодно применять вторую стратегию (реклама и исследование). За один квартал до перехода на новую модель целесообразно прекратить и рекламу и исследования. Если же начальным было состояние S1 , то рекламу и исследования следует применить лишь два первых квартала, затем следует освободившиеся средства употребить на подготовку производства новой модели. Таким образом, и при удачной и неудачной моделях оказывается все же выгодным начинать производство, обеспеченное как рекламой, так и исследованиями. Заметим, что в данном случае не был ясным вопрос о том, с какой вероятностью наступят состояния S1 и S2 . Для этого следовало бы ввести вектор начальных вероятностей, что несколько усложнило бы вычисление. Описанный выше метод, как указывалось выше, обладает сравнительной простотой, но при малом числе этапов. Кроме того, в этом методе несколько затруднен процесс автоматизации расчетов на ЭВМ.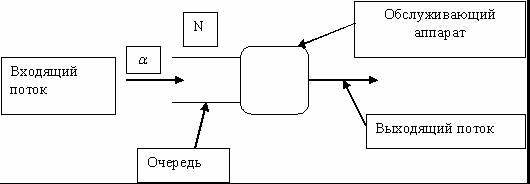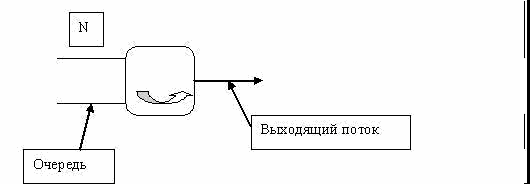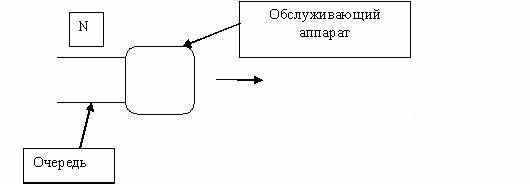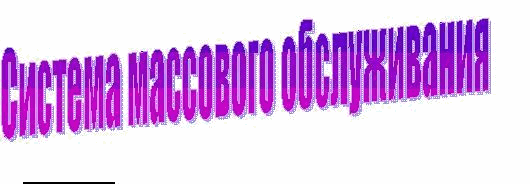
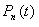, или вероятностью продолжительности промежутка между
поступлениями двух соседних требований: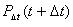 
. Поток требований является внешним воздействием на систему массового обслуживания.
Обслуживающий аппарат мажет обслуживать каждое требование или одновременно группу требований (обслуживание индивидуальное или групповое).
Время обслуживания может быть детерминированным (постоянное) и случайным (встречается наиболее часто). Вероятность обслуживания чаще
всего подчиняется показательному закону распределения вероятностей.
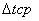- среднее время обслуживания требований.
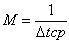- скорость обслуживания.
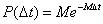,где t - время, в течении которого обслуживается требование. Вероятность появления n требований за t времени для потока
требований, образующих простейший Пуассоновский поток, определяется по формуле: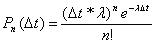 
. Порядок поведения требований в очереди называется дисциплиной
очереди.
Входящий поток и время обслуживания.
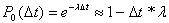- вероятность отсутствия требований за t времени.
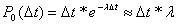- вероятность появления 1-го требования.
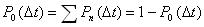- вероятность обслуживания одного требования за времени.
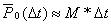- вероятность того, что за времени требование не будет обслужено.
:
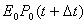в момент времени t – требование отсутствует
полная группа событий
в момент времени t – одно требование.
Полная вероятность отсутствий.
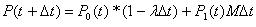, где
Е1 – в системе находится одно требование в течение t времени.
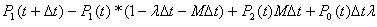Еn – в системе находится n требование в течение t времени.
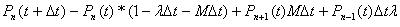Стационарная вероятность – такая вероятность, которая не зависит от времени. Следовательно, при этом Pn(t)=const, a P’n(t)=0.
Принимая условия стационарности, определим коэффициент загрузки 
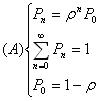
Среднее число требования в системе: 
Дисперсия или квадрат отклонения среднего числа требований: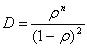 
Средняя длина очереди: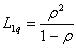 
Среднее время ожидания обслуживания: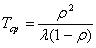 
Максимальная длина очереди: