Paper on master's dissertation theme

R-Neocognitron is losing its effectiveness on big number of classes to which input images can belong. It happens because the time of recognition is increasing with the number of neurons.
TD-R-Neocognitron performs so-called "mental rotation" of the input image, determining the angle and comparing it with template. This principle is common to behavior of human's visual system: when human being is watching a picture that is rotated to 90 degrees, he determines the angle and tries to rotate he's head to realize what is shown on the picture.

Present methods overview

At this moment there are many versions of neocognitrons' realization, which have marginal differences:

1. models based on the "unsupervised" method of learning
2. models based on the "supervised" method of learning [3]

Last ones have a higher speed of learning process and stability. But their disadvantage is the need for use of additional information about belonging of all the input image and its features to one or another class.

Models which study "without a teacher" are more adaptive and optimal. They are based on the conception of human beings' visual system.

Structure of neocognitron

The neocognitron is a multilayered self-organizing neural net, which models visual nervous system of human beings. Its layers consist of many neurons formed into planes – two-dimensional arrays. Neuron of a layer receives its input signals from a limited number of neurons from a previous layer, and sends its output signal to the next layer.[3]

There are three types of neurons which are used in the neocognitron - S-neurons (“simple” neurons), C-neurons (“complex” ones) and inhibitory neurons. Layers are grouped in pairs. Each S-layer which consists of S-neurons is followed by a C-layer. Planes of every S-layer are trained to recognize certain feature of an input image; planes of a C-layer arrange the results of recognition.

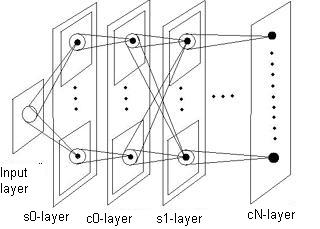
The number of neurons in planes decreases from a layer to layer. The last C-layer contains of many planes with only one neuron in a plane; each of this neurons responds to the certain input image class. Input layer contains only one plane, and sends the consistency of input signals to the first S-layer.

Each plane of a S-layer receives its input signals from all the planes of a previous C-layer, i.e. each neuron in every S-plane is connected to the groups of neurons from all C-planes located in the same areas. Neurons of C-layers’ plane receive input signals only from the group of neurons from respective S-plane.

Every neuron responds to the output signals of neurons from previous layer which are located in its connection area. The deeper the level of a layer, the larger becomes its receptive field. Hence, each neurons contained in the last C-layer responds to the whole input layer. Size of a connection area is so determined as to cover the whole of input layer. Connection areas of neurons located in small area can cover each other.[1]

Description of Neurons

All the neurons which are used in neocognitron are analogous, i.e. their input and output signals signals take non-negative real values. Only 3 types of neurons are employer in neocognitron – S-neurons, C-neurons and inhibitory ones.

Lets consider the functioning of a S-neuron. As shown on Figure 2, it receives many excitatory input signals from neurons of C-layer – U(k), which increase its output signal. On other hand, the influence of inhibitory neuron’s output signal, V, decreases its respond. Each connection with a neuron from previous layer has its own positive coefficient – a(k). Coefficient of a connection with inhibitory neuron denoted as b.

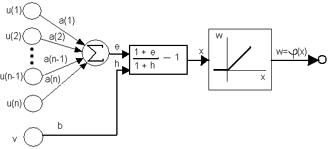
Lets denote the output signal of the S-neuron as W. Its calculated by the equation in Figure 3:

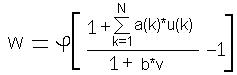
Function of activation is linear on positive values of input signal, and equal 0 otherwise. Only a(k)- and b-coefficients are being reinforced when net is self-organizing.

Inhibitory neuron has the same receptive field as S-neuron.

The output of an inhibitory neuron is calculated be the equation in Figure 4:

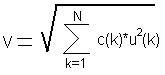
The coefficients of the connections from C-layer to inhibitory neuron are fixed and do not change; their values decreases from the middle of the receptive field to its borders, so that their sum equals 1.[1]

Lets consider calculus, concerned with C-neuron proceeding. Coefficients of interconnections from S-layer to C-layer are defined once and do not change during the procedure of self-organizing; their values are being determined similarly to inhibitory neurons. The output value of a C-neuron are determined by the formula:

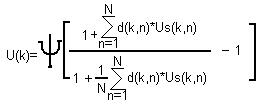
Where Ksi-Function gives x/a+x with x>0 and 0 otherwise

Self-organizing

The neocognitron is trained by unsupervised method, a “learning-without-a-teacher”, i.e. no instructions about a class to which the input image belongs is needed. Learning is processed step by step, from one layer to another.

As was mentioned above, only a(k) and b-coefficients of a S-neuron are being reinforced by formula

where q1 is a positive constant which determines the speed of increment, u(k) is the output of Kth neuron in a C-layer, c(k) - weight coefficient of inhibitory neuron, v - output of inhibitory neuron[2]

Coefficients of a(k) and b are near zero at the beginning of training process.

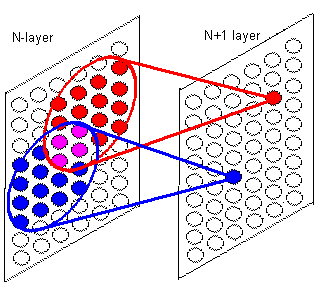
Process of learning is directed to make each single neuron plane of an S-layer respond to a different feature of input image. But some situations can appear when neurons of different planes can produce high enough output values and increase their weight coefficients while studying on the same patterns. Competitive columns were employed to avoid that. For each neuron some area of a certain size is selected. This area includes a number of neurons' neighbors and is called a slice-area for on of a columns. Neurons of the same area from other planes of the layer are involved in this column too. Columns, as the connection fields, can cover each other.

When output signals for all the neurons of an S-layer are calculated, the candidate for each competition column is being selected. This neuron is the neuron with maximum output value. It is being written to the candidates list of the plane where it is situated. After that candidate with maximum output value is being selected from each planes' list, and its weight coefficients are being incremented. This coefficients then copied to all neurons of this plane. Thus, neurons of only one plane is being educated to respond to a certain feature of an input image.[1]

Current results

At this moment system which successfully recognizes Arabic digits has been realized. Algorithm of input image reading and recognition has been developed, just as algorithm of learning. Tests of the working system has been held. On the computer Intel Celeron 900Mhz processor the process of learning on the images of 19x19 size has taken 10.3 seconds. During this process each image has been given to the net for 100 times. The process of recognition of images of the same size takes 0.1 second. Neocognitron has recognized position- and shape-shifted images successfully.

At this time the automated process of learning on the set of images is being developed. The researches of the neocognitron characteristics improvement are being performed.

Conclusion

Neocognitron has shown very good results on image recognition. The development of this neural net is a very perspective task, and its solution will allow the creation of the universal system for different objects' identification. The system has some disadvantages at this time, such as low speed of learning, strict parameters of input images. But these problems are solvable.

List of Literature

1. Fukushima K. Neocognitron: a self-organising neural network for mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics 36, 1980, pp. 193-202.
2. Fukumi, S. Omatu, and Y. Nishikawa, Rotation-Invariant Neural Pattern Recognition System Estimating a Rotation Angle, IEEE, Trans., Neural Network, 8, 1997, pp. 568-581.
3. D. R. Lovell, A. C. Tsoi and T. Downs, "A Note on a Closed-form Training Algorithm for the Neocognitron," To appear in IEEE Transactions on Neural Networks.
4. S. Satoh, J. Kuroiwa, H. Aso and S. Miyake, "Recognition of Hand-written Patterns by Rotation-invariant Neocognitron," Proc. of ICONIP'98, 1, pp. 295-299, 1998.
5. S. Satoh, J. Kuroiwa, H. Aso and S. Miyake, "Pattern Recognition System with Top-Down Process of Mental Rotation," Proc. of IWANN'99, 1, pp. 816-825, 1999.