Введение

В современном мире все большее значение приобретает информация, ее способы представления и распространения. Зрительное восприятие информации является основным способом получения человеком представлений об окружающем мире. Поэтому задачи компьютерной графики приобретают особое значение в современном информационном обществе, основной движущей силой которого является наука.

Среди основных задач компьютерной графики в научной сфере можно выделить такие:

Одной из важнейших научных задач является проведение исследования какого-либо явления или объекта. При этом важно иметь компьютерную модель изучаемого предмета. В реальном мире все физические объекты можно разделить с точки зрения компьютерной графики на два класса: простые, такие как куб, шар, тор, и сложные, то есть те, которые нельзя представить с помощью простого математического описания (поверхность Земли, лицо человека и пр.). Если получение модели простого объекта не составляет особого труда, то представление предмета сложной геометрической формы является комплексной задачей, подключающей средства таких областей знаний как аналитическая геометрия в пространстве, аналитическая алгебра, дискретная математика и пр. Геометрически сложные объекты составляют подавляющее большинство исследуемых объектов, и, как правило, они задаются точками в пространстве. В связи с этим возрастает актуальность решения задачи восстановления поверхности по произвольному набору точек [1].

Цель и задачи работы

Цель и задачи выпускной работы состоят в получении программной системы, позволяющей построить сеточную модель сложной поверхности по набору точек в трехмерном пространстве, и оценке ее быстродействия.

С точки зрения формального описания, задачу построения сеточной модели по множеству точек в трехмерном пространстве можно представить следующим образом. Получить поверхность S’, которая аппроксимирует неизвестную поверхность S с использованием множества точек в трехмерном пространстве P = {p_i | i=1..n, n≥3}, величины допустимого отклонения δ и плотности расположения точек ρ.

Научная новизна

Научная новизна данной работы заключается в создании программного комплекса, реализующего усовершенствованный метод восстановления сложных поверхностей в пространстве по набору точек на основе метода «marching cubes».

Практическая ценность

Практическая ценность результатов выпускной магистерской работы состоит в том, что система может быть использована в системах медицинской диагностики, виртуальной реальности, а также для работы трехмерных сканеров для считывания разных объектов сложной формы.

Обзор существующих исследований и разработок по теме

Jordi Esteve, Pere Brunet и Alvar Vinacua ` в статье [ 4 ] , опубликованной в августе 2005 года, описали метод получения замкнутой поверхности, которая аппроксимирует произвольное множество точек, заданных в 3D пространстве. Описанный метод в качестве входных параметров не требует ни топологические отношения между точками, ни нормаль к искомой поверхности. Кроме того метод не имеет своей целью точно интерполировать искомую поверхность, однако приближает полученную поверхность со строго фиксированной максимальной ошибкой.

Исходные точки могут быть получены различными путями с помощью оптических, ультразвуковых или осязательных сенсоров, часто используемых в качестве источника данных. Программы геометрического моделирования должны обработать это множество точек таким образом, чтобы получить аппроксимирующую поверхность. В таком случае:

• сгенерированная поверхность будет более компактной, чем исходное множество точек;
• будет осуществлена более реалистичная визуализация;
• при работе с полученной поверхностью будут доступны простые геометрические операции.

Разработанный авторами алгоритм позволяет восстанавливать поверхность какого-либо замкнутого твердотельного объекта. Основные этапы алгоритма следующие:

1. Разбиение области пространства, содержащей точки множества, на воксели (воксель - единицы пространства, кубик с достаточно малой длиной ребра). Отнесение вокселей к группе внутренних («тяжелых») или нет («легких») кубиков.

2. Построение дискретной замкнутой мембраны. Множество шестисвязных (соседствующих с гранями заданного вокселя) вокселей, которые образуют результирующую поверхность. В самом начале построения мембрана имеет форму «кирпича». Шаг за шагом мембрана сужается, пока выполняется определенное условие.

3. Сглаживаение дискретной мембраны для получения гладкой поверхности.

4. Построние результирующей поверхности по полученной дискретной мембране.

Можно выделить следующие преимущества предложенного алгоритма:

• воссоздание поверхностей по набору точек с неравномерной плотностью;
• воссоздание объектов, которые содержат несвязанные замкнутые оболочки;
• метод гарантирует получение результирующего замкнутого объект а;
• аппроксимация с ограниченной величиной ошибки поддерживающая сглаживание

В статье [5] Hugues Hoppe и др. описан и представлен алгоритм, который принимает в качестве входного параметра неорганизованное множество точек лежащего внутри или около неизвестного множества М, и выдает в качестве результата упрощенную поверхность, которая аппроксимирует М. Предполагается, что заранее не известны ни топология и наличие границ, ни геометрия М, — все автоматически выводится из данных. Эта проблема естественно возникает в разнообразных практических ситуациях, таких как сканирование объекта с различных точек наблюдения, восстановление биологических форм из двумерных срезов, интерактивное эскизирование (зарисовка) поверхности.

В широком смысле, интересующий класс задач может быть определен как следующий: по заданной частичной информации о неизвестной поверхности построить наиболее компактное из возможных представление поверхности. Подобные проблемы воссоздания возникают в различных научных и инженерных прикладных областях, включая:

- Поверхности, построенные по данным области. Данные, полученные системой лазерного сканирования, обычно являются прямоугольной сеткой расстояний от сенсора до сканируемого объекта. Если сенсор и объект неподвижны, только объекты, находящиеся в поле зрения, могут быть полностью оцифрованы. Более совершенные системы, например, такие, которые производит Cyberware Laboratory, могут оцифровывать цилиндрические объекты, вращая либо сенсор, либо объект. Однако, топологически более сложные объекты, например, обычная кофейная чашка с ручкой, не могут быть представлены в совершенстве ни одним из этих методов. Для получения качественного представления объекта при помощи сканера, нужно использовать достаточно много точек наблюдения. Объединение данных, полученных из различных точек, с целью построения многогранного представления поверхности – это нетривиальная задача.

- Поверхности, построенные из контуров: В медицинских исследованиях часто используется метод среза биологических образцов (тканей) на тонкие слои при помощи микротома. Очертания интересующих структур затем оцифровываются для создания стека контуров. Задача сводится к восстановлению трехмерной структуры по стеку двумерных контуров. Хотя этой задаче уже было уделено много внимания, существующие методы ее решения содержат жесткие ограничения. Возможно, в первую очередь, среди них можно выделить сложность работы с ветвящимися структурами.

- Интерактивное эскизирование (зарисовка) поверхности. Многие исследователи изучили создание кривых в R² при помощи трассировки пути пера или мышки, в то время, как пользователь набрасывает эскиз желаемой формы. Была описана система позволяющая создавать произвольные кривые в R³ при помощи записи движения пера, оснащенного сенсором Полхемуса. Функциональность этой системы может быть расширена до проектирования произвольных поверхностей, игнорируя порядок записей позиций, давая таким образом возможность водить пером вперед и назад по поверхности. Задача сводится к построению представления поверхности, включающей неорганизованную совокупность точек.

Алгоритмы воссоздания поверхностей, решающие вышеописанные задачи, как правило, разрабатывались от случая к случаю для использования частичной структуры данных. Например, алгоритмы создания поверхности по набору контуров делает сложным использование данных, организованных в контуры (т.е. замкнутые полигоны), и того факта, что контуры лежат на параллельных плоскостях. Аналогично, алгоритмы, специализированные на воссоздании поверхностей по данным, полученным из различных точек наблюдения, должны учитывать соседство точек внутри каждого представления.

В качестве сравнения, подход Hugues Hoppe имеет своей целью поставить общую задачу, которая не будет привязана ни к одной из структур точек данных. Этот подход имеет как теоретическую, так и практическую ценность. С точки зрения теории, абстрагирование до общей проблемы часто проливает свет на истинно критические аспекты проблемы. С практической точки зрения, один алгоритм, решающий общую задачу, может быть использован для решения каждой конкретной подзадачи.

Предложенный алгоритм состоит из двух этапов. На первом этапе определяется функция f: D -> R, где D, заключенное в Rß,- это область около данных, такая что, f оценивает геометрическое расстояние до неизвестной поверхности M. Вводится множество нулей Z(f) в качестве оценки для аппроксимации М.

На первом этапе используется подзадача построения плоскости, наименее удаленной от совокупности точек. Она составляют основу, на которую опираются все дальнейшие этапы работы. Основными параметрами плоскости являются базовая точка, через которую проходит плоскость, а также нормальный вектор плоскости, что можно записать как пару ( c, n). Базовая точка получается путем нахождения геометрического центра массива точек подмножества.

Для определения же нормального вектора необходимо решить экстремальную задачу, где параметром минимизации является сумма квадратов расстояний от каждой точки множества до плоскости (метод наименьших квадратов).

 

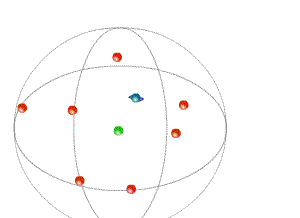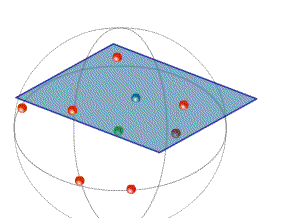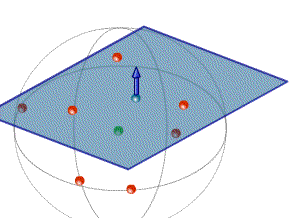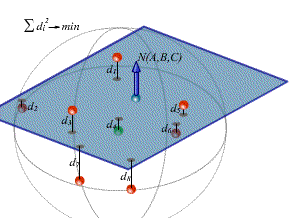
Удобным для реализации является представление параметра минимизации в виде функции Лагранжа [2] , где к сумме квадратов расстояний добавляется выражение, значение которого фактически равно нулю. Задача нахождения экстремума сводится к решению системы уравнений, формируемых из частных производных функции Лагранжа по неизвестным, приравненных к нулю. Решение полученной системы сводится к нахождению множителя Лагранжа, который является собственным числом выведенной из системы матрицы. Метод решения системы подробно описан в книге Бугрова Я.С. и Никольского С.М [3].

На втором этапе используется контурный алгоритм для того, чтобы аппроксимировать Z(f) симплициидальной поверхностью.

Ключевая составляющая для определения функции знакового расстояния – это ассоциирование ориентированной плоскости с каждой из точек. Эти плоскости касания используются как линейные аппроксимации к поверхности. Хотя конструкция касательных плоскостей относительно проста, выбор их направлений, так же как и определение глобально-совместимой ориентации для поверхности – это одно из основных препятствий, с которыми приходится сталкиваться в алгоритме. Плоскости касания не напрямую определяют поверхность, хотя их объединение может иметь сложную структуру. В алгоритме плоскость касания используется для того, чтобы определить функцию вычисления знакового расстояния до плоскости.

В качестве заключительного этапа, трассировки контура, была выбрана вариация известного алгоритма «марширующие кубы», который позволяет представить функцию в вершинах кубической сетки и найти контурные пересечения внутри тетраэдрической декомпозиции кубических ячеек. Для эффективной оценки границ, размер ребра куба должен быть не меньше суммы заданных величин ошибки аппроксимации и плотности точек. На практике часто удобно брать значение ребра больше этой величины для того, чтобы ускорить процесс вычисления и уменьшить число сгенерированных граней.

Перечень нерешенных проблем

В данной предметной области можно выделить ряд нерешенных проблем, среди которых:

•  проблема определения нормалей плоскостей (выбор одной из двух);
•  проблема построения сетки при неравномерном расположении точек;
•  проблема повышения скорости работы алгоритма;
•  проблема восстановления сложной поверхности в реальном времени, имеется в виду случай, когда новые координаты точек поступают по ходу решения задачи.

Текущие и планируемые результаты по теме

Текущим результатом работы является система построения множества плоскостей по произвольному набору точек, разработанная в среде NetBeans 4.1 на языке Java, а также разработана структура программной системы восстановления поверхности по точкам в среде Rational Rose 7.0 (модули, классы системы и их взаимосвязь). Планируется программно реализовать данную систему, оценить ее эффективность, задавая различные входные параметры.

Заключения и выводы

Список литературы

1. Хромова Е.Н., Пауков Д.П., Башков Е.А. Воссоздание поверхности по произвольному набору точек. Подзадача построения плоскости, наименее удаленной от совокупности точек» ІІ Республіканська наукова конференція студентів , аспірантів та молодих вчених «Комп ’ютерний моніторинг та інформаційні технології» Донецк ДонНТУ 15 мая 2006г.

2. Никулин Е.А. Компьютерная геометрия и алгоритмы машинной графики. – СПб.: БХВ-Петербург, 2003. – 560 с.: ил.

3. Бугров Я.С., Никольский С.М. Дифференциальное интегральное исчисление: Учебник для вузов. - М.:Наука, 1988 - 431с.: ил.

4. Jordi Esteve, Pere Brunet and Alvar Vinacua ` Approximation of a Variable Density Cloud of Points by Shrinking a Discrete Membrane, Universitat Polit`ecnica de Catalunya, Barcelona, August 2005

5. Hugues Hoppe Tony DeRose Tom Duchamp John McDonald Werner Stuetzle Surface Reconstruction from Unorganized Points University of Washington 1992