Аннотация

 Аннотация Формализовать , и прогнозировать позвоночника на различные воздействия возможно с помощью динамической модели позвоночника методов математического моделирования . Для восстановления поверхности позвонка используется ТИС , по частичным данным о форме вычисляются недостающие точки поверхности . Для ускорения работы алгоритма используется Быстрого Преобразования Фурье (БПФ ) при расчете сумм ТИС . Ключевые слова : Моделирование , Восстановление поверхности , Интерполяция , Тригонометрические Интерполяционные Суммы (ТИС ), Сплайновая .

 1. ВВЕДЕНИЕ

Тело позвонка – очень сложная геометрическая фигура, имеющая большую степень нелинейности, что затрудняет ее представление в электронном виде. В связи с этим целесообразно уменьшить размерность массива данных для хранения этой структуры в компьютерном представлении с наименьшими потерями для последующего воспроизведения формы позвонка. Следовательно, при отображении графической информации целесообразно использовать алгоритмы геометрической интерполяции и восстанавливать форму тела позвонка посредством Тригонометрических Интерполяционных Сумм (ТИС). Математический аппарат ТИС хорошо зарекомендовал себя при восстановлении сложных, анатомических структур [4]. Алгоритм дискретного преобразования Фурье, который лежит в основе ТИС, позволяет учитывать сложные поверхности с нелинейностью высоких порядков, что дает ему значительное преимущество по сравнению со сплайновой интерполяцией. Так как сплайн-функция строится полиномом третьей степени, то есть по четырем точкам, то отдельные отрезки сплайнов приходится «склеивать». Целью данной работы является создание математической модели, описывающей геометрические параметры позвоночника и условия их изменения во времени и в пространстве с ее графической визуализацией.

 2. ТРИГОНОМЕТРИЧЕСКИЕ ИНТЕРПОЛЯЦИОННЫЕ СУММЫ

Наиболее простыми и широко используемыми методами представления изображений являются методы, основанные на объёмных элементах или триангуляции. Хотя эти методы показывают хорошее представление на многих обработках биомедицинских изображений и заданиях анализа, их полезности препятствуют большие требования к памяти, отсутствие понятий контура, поверхности и параметризации объекта, и тот факт, что они не применимы в приложениях, где требуется более высокий порядок непрерывности представления. Краткое описание применяемого математического аппарата: Дано множество GC(N 1 +1)(N 2 +1) точек образца (гладкой) поверхности M анатомической структуры, выбор параметрического представления заключается в определении координатных функций x(u 1 , u 2 ), y(u 1 , u 2 ) и z(u 1 , u 2 ), определённых на квадрате U=[0,1]x[0,1] таким образом, что K(N 1 ,N 2 ) преобразуется на G. Данный математический аппарат хорошо применим, как для плоских, так и для трехмерных объектов, но при этом возникают трудности в представлении входных данных для функций ТИС, так как они задаются набором точек, упорядоченных по контурам. Данная проблема решается путем задания параметризации, и соответственно исходных данных, относительно контура объекта.

3. ПРИНЦИПЫ ПОСТРОЕНИЯ МОДЕЛИ ПОЗВОНОЧНИКА

Более сложной задачей является графическое динамической модели позвоночника . Разработанная модель позвоночника базируется следующих концепциях .

 3.1 Статическая модель

Исходными данными являются данные, снятые с рентгенограмм пациентов [2]. Позвоночник рассматривается как кинематическая цепочка позвонков. Выходными данными такой модели являются рассчитанные параметры позвоночника:

- высота тела позвонка;
- угол наклона тела позвонка в сагиттальной и фронтальной плоскости;
- высота диска;

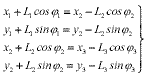
  ,где Li – длины позвонков, а φi – углы наклона тел позвонков к оси (OX), точки Сi - центры инерции позвонков.

 Приведенные уравнения связывают звенья воедино. В механике они называются уравнениями связей. Так как каждое из свободных звеньев имеет три степени свободы, то система из трех свободных звеньев имеет девять степеней свободы. Уравнения связей дают возможность выразить какие-нибудь пять опорных координат через оставшиеся четыре, поэтому для определения положения трехзвенной модели достаточно пять из девяти опорных координат. Модель имеет пять степеней свободы. 3.3 Кинематическая модель Позвоночник представляется в виде гибкого стержня. В этом случае используется модель, описывающая деформации гибкого стержня. Такая модель основана на матричных преобразованиях. Напряженно – деформируемое состояние каждого сечения модели описывается вектором состояния Z.

где Ui - продольное перемещение , Wi - поперечное перемещение , i - угол , а Mi - изгибающий момент , Qi - поперечная сила , Ni - осевая сила .

 Связь между начальными значениями параметров состояния и их значениями в некотором сечении представляется с помощью цепочки матриц уравнением, где А – цепочка переходных матриц, элементы которых содержат значения: массы, момента инерции, круговой частоты, площади поперечного сечения, жесткости и длины элемента модели (позвонка). Каждая матрица интерпретирует отдельный позвонок, таким образом, последовательное перемножение матриц дает цепочку взаимодействующих элементов (позвоночник). При изменении какого-либо параметра одной из матриц вносятся изменения в значения последующих элементов матриц и соответственно конечного результата. Для вычисления изменений предыдущих элементов следует последовательно решать обратное уравнение, где X – предыдущий измененный элемент, деформации в который вносит элемент Ai. Это уравнение итерационно решается до первого элемента. Проводя аналогию между геометрическими и физическими параметрами поведения гибкого стержня и позвоночника, можно предложить создание новой модели.

4. ДИНАМИЧЕСКАЯ МОДЕЛЬ ПОЗВОНОЧНИКА

Такая динамическая модель строится в два этапа : сначала по определенному набору строится каждый позвонок , затем набор соединяется в единую цепочку взаимодействующих звеньев – позвоночник .

4.1 Восстановление поверхности позвонка

Для детальной и отображения каждого позвонка используется математический аппарат ТИС , по
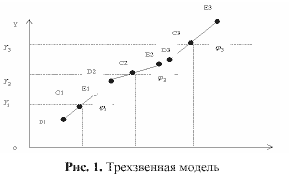
частичным данным о форме позвонка с помощью ТИС интерполяции вычисляются недостающие точки . По полученному массиву точек строится поверхность позвонка . Для ускорения работы алгоритма используется Быстрого Преобразования Фурье (БПФ ) при расчете сумм ТИС [3]. Пример построения поверхности одного представлен на Рисунке 4. Исходными данными координаты упорядоченных точек контуров , полученных с рентгенограмм препаратов позвонков [1], пример такого контура представлен на Рисунке 2.

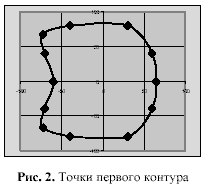
Поверхность, построенная по исходному набору точек, представлена на Рисунке 3.

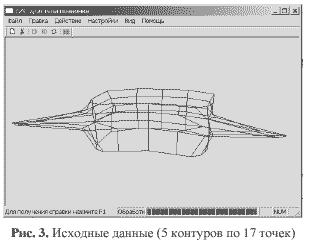
 Результат работы программы показан на Рисунке 4

 4.2 Представление формы позвоночника

Для представления формы всего позвоночника используется сплайновая интерполяция. По данным, полученным в ходе вычисления переходных матриц (кинематическая модель), или по координатам отрезков хорд (статистическая модель) строится сплайновый полином. При этом требуется знание параметров не в каждой, а только в трех ключевых точках (основных отделах позвоночника). В качестве критерия адекватности модели реальным данным использована визуальная экспертная оценка. Применение сплайновой интерполяции значительно снижает временные затраты на вычисления переходных матриц, а следовательно на отображение модели. На данном этапе разработки реализована графическая интерпретация модели позвоночника, представленного в виде кинематической цепочки элементов с расчетом основных диагностических параметров. Пример работы программного средства представлен на Рисунке 5.

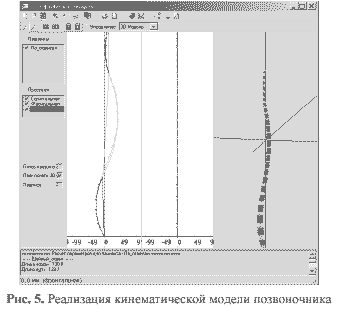
 5. ЗАКЛЮЧЕНИЕ

В разработанной модели учитываются геометрические особенности строения позвонков человека, а также изменения его кинематических характеристик в пространстве и во времени. Использование этой модели позволит наблюдать деформации всего позвоночника при изменении одного или нескольких произвольно выбранных параметров. При этом геометрические характеристики, необходимые для расчетов цепочки матриц А * второй модели, являются результатом вычислений первой модели. Данную модель можно использовать для наблюдения реакции позвоночника на различные воздействия: ходьба, различные нагрузки, хирургическое вмешательство, столкновение автомобилей, и.т.д. Графическая интерпретация модели позволит конечным пользователям, задав начальные параметры позвоночника, получить его трехмерное изображение, перемещать, вращать, задавать направление действующих на него нагрузок, отслеживать изменение формы позвоночника при физиологических движениях и ходьбе. Графическое представление позвоночника производится путем моделирования взаимодействующей цепочки позвонков.

Выводы:
• Использование алгоритма ТИС и методов сплайновой интерполяции позволяет адекватно отразить форму каждого позвонка и всего позвоночника в пространстве и производить расчеты без потери качества отображения.
• Использование такой модели позвоночника позволит решать вопросы прогнозирования течения деформации и результатов оперативной ее коррекции.

6. БИБЛИОГРАФИЯ

[1] Гладков А. В., Гусев А.Ф. Морфометрия позвоночника. В кн.: Повреждения и заболевания позвоночника. Л.-1986 стр. 84-92.

[2] Гладков А. В., Пронских И.В. позвоночного столба . В кн .: Актуальные
вертебрологии Л.- 1988. стр . 114-116.

[3] Нуссбаумер Г. Быстрое Фурье и алгоритмы вычисления сверток . – М.: и связь , 1985. – 248с .

[4] Фроловский В.Д., Фроловский Д.В. и развертка поверхностей общего вида // Материалы 8-й Всероссийской научно -практической конференции по графическим информационным технологиям «КОГРАФ -98». - Н.-Новгород : НГТУ , 1999.-С.120-121.

5] Jimenez J.C., Biscay R., Aubert E. Parametric representation of anatomical structures of the human body by means of trigonometric interpolating sums // Journal of Computational Physics. 1996. № 0135.-p.120-155.

[6] White A.A., Panjabi M. Clinical Biomechanics of the Spine. 1978, 536p.