Реферат выпускной работы магистра по теме
"Моделирование системы управления запасами"*
Колесниковой Я. А.
- ВВЕДЕНИЕ
- 1 АНАЛИЗ СОСТОЯНИЯ ПРОБЛЕМЫ
- 1.1 Проблема управления запасами
- 1.2 Система управления запасами с постоянным контролем
- 1.3 Скоропортящиеся запасы
- 1.4. Скидка на продажную цену товара для системы с периодическими проверками уровня запаса
- 2. РАЗРАБОТКА МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ СО СКИДКОЙ ДЛЯ СИСТЕМЫ С ОПЕРАТИВНОЙ ИНФОРМАЦИЕЙ ОБ УРОВНЕ ЗАПАСА
- ВЫВОДЫ
- ПЕРЕЧЕНЬ ССЫЛОК

В данной работе рассматривается разработка (Q, r)-системы управления товарными запасами, предназначенная для небольших магазинов розничной торговли. Актуальность данной системы обусловлена необходимостью повышения конкуренции в сфере розничной торговли, что невозможно без создания, освоения и внедрения соответствующих инструментов для решения экономических задач. Поскольку малые и средние предприятия зачастую ограничены в денежных средствах, актуальной является разработка систем, автоматизирующих отдельные аспекты работы предприятия.
К одним из таких инструментов относятся автоматизированная система учета товаров на складе и система управления запасами. Зачастую планирование пополнения запасов необоснованно ведется по некоторым жестко установленным нормативам, независимо от того, насколько экономически оправдан данный уровень запаса в данной конкретной ситуации. Такой подход приводит к заведомо завышенному уровню запасов, что означает неоправданное отвлечение финансовых ресурсов и снижение их оборачиваемости [1]. Поэтому автоматизированная система управления запасами предприятия с одной стороны, не является слишком дорогостоящей, а с другой, может значительно повысить эффективность работы предприятия.
При наличии автоматизированной системы учета, система управления запасами должна основываться на модели управления запасами с постоянным контролем уровня запаса, т.е. система, в которой каждый раз, когда уровень запаса опускается до r, подается заявка на заказ размером Q.
Большинство рассматриваемых в литературе систем управления запасами являются однофакторными. В связи с вычислительной сложностью подобных задач, рассматриваются либо отдельные элементы систем управления запасами, либо их комбинации, не позволяющие учитывать все основные элементы системы управления запасами, такие как скидки, дефицит запасов, устаревание запасов, ограниченная площадь склада или определенная сумма, выделенная на формирование запасов.
Целью магистерской работы является создание комплексной системы управления запасами готовой продукции, позволяющей малому либо среднему предприятию, занимающемуся розничной торговлей, полностью автоматизировать управление запасами.
В рамках магистерской работы разработан алгоритм определения скидок на продажную цену продукции с целью уменьшения объема списываемых товаров, возникающих в связи с ограниченным сроком их использования. Планируется также разработать алгоритм, позволяющий распределить во времени заказы товаров различной номенклатуры с учетом ограничений на вместимость склада и максимальную сумму, выделенную на управление запасами.
1.1 Проблема управления запасами
Управление запасами представляет собой сложный комплекс мероприятий, направленный на обеспечение бесперебойного процесса производства и реализации продукции при минимизации текущих затрат на обслуживание запасов [2].
О. Пестрецова [3] описала основные затраты и потери в связи с хранением запасов и их отсутствием, которые можно представить в виде следующей таблицы.
Таблица 1. – Затраты, возникающие в связи с хранением или отсутствием запасов.
| Хранение запасов | Отсутствие запасов |
|---|---|
| замороженные в запасах финансовые средства; | потери от простоя производства; |
| расходы на содержание специально оборудованных помещений; | потери в связи с отсутствием товара на складе в момент предъявления на товар спроса; |
| оплата труда специального персонала; | потери от закупок товаров мелкими партиями по более высоким ценам; |
| затраты, учитывающие постоянный риск порчи, хищений, а также моральное и физическое старение запасов; | потеря или сужение рынка сбыта товарной продукции; |
| затраты, связанные с колебаниями конъюнктуры рынка. | нарушение производственных связей с предпринимателями. |
Поэтому политику управления запасами можно свести к двум вопросам: когда заказывать и в каких количествах.
1.2 Система управления запасами с постоянным контролем
Выделяют две основные системы управления запасами: систему с постоянным контролем и систему с периодическими проверками [4].
В системе с периодическими проверками подсчет запаса производится периодически (раз в день, неделю, месяц), и в зависимости от уровня наличного запаса производится заказ определенной партии продукции.
При наличии автоматизированной системы учета, система управления запасами может основываться на модели управления запасами с постоянным контролем уровня запаса, т.е. система, в которой каждый раз, когда уровень запаса опускается до r, подается заявка на заказ размером Q.
Теоретические основы такой системы достаточно подробно изложили Хедли и Уайтин [4]. Позже были написаны и другие работы, содержащие различные варианты описания (Q, r)-системы управления запасами, в том числе с различными вариантами учета дефицита, ограниченного срока годности товаров, описывались точные и приближенные модели [5-10].
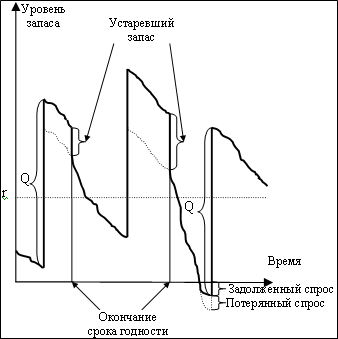
При детерминированном и случайном спросе динамика запаса описывается рисунками 1 и 2 соответственно.
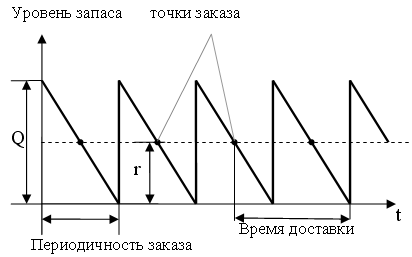
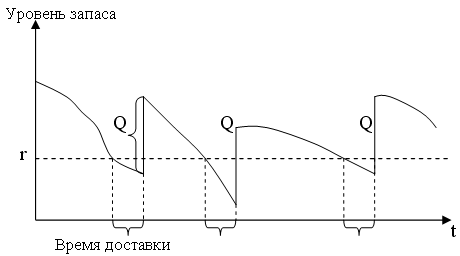
1.3 Скоропортящиеся запасы
1.3.1 Точное управление скоропортящимися запасами
Скоропортящийся запас – это запас в котором все единицы одного товара, оставшиеся на складе, одновременно потеряют свою полезность [5]. Оставшиеся единицы должны быть выброшены, если они еще не были использованы после хранения в течение фиксированного промежутка времени. Поэтому управление запасами скоропортящихся товаров происходит следующим образом:
- 1) определяется оптимальный размер заказа (с учетом расходов на хранение, на дефицит и списание устаревших товаров) и подается заказ на пополнения запаса;
- 2) весь прибывший продукт считается новым;
- 3) отпуск товара производится по принципу «первый пришел – первый вышел»;
- 4) продукт, не реализованный в течение срока хранения, m, списывается.
Для точного описания наличного запаса в каждый момент времени и уровня запасов в системе используются формулы (1) и (2) соответственно [10]:
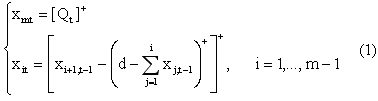
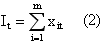
где xti – количество запасов на момент времени t с оставшимся сроком хранения равным i;
m – срок годности продукта;
d – спрос на товар ;
(a)+=max(0,a).
Тогда, для (Q,r)-системы управления запасами можно вывести соотношения позволяющее определить средние издержки в единицу времени i при цене p определяются по формуле (3):
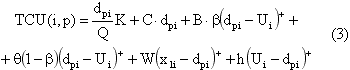
где dpi – спрос на товар ценой р за время i;
K – фиксированные затраты на оформление заказа;
C – затраты на пополнение единицы запаса;
G – затраты, связанные с учетом неудовлетворенного спроса (за единицу);
b – доля неудовлетворенного спроса, которая может быть задолжена;
q – затраты, связанные потерей неудовлетворенного спроса (за единицу);
W – затраты, понесенные вследствие устаревания товара (за единицу);
h – затраты на содержание единицы запаса в единицу времени.
1.3.2 Приближение уровня устаревших товаров
Использование формулы (1) при создании программного продукта, предназначенного для решения реальных задач управления запасами, практически невозможно, в связи со значительной вычислительной сложностью, вызванной использованием данной формулы. Поэтому целесообразно использовать приближенный подход для описания наличного запаса в каждый момент времени, описанный в [9].
При формировании приближенного значения уровня запаса в каждый момент времени, используются следующие предположения:
- 1) В данной системе рассматривается только один скоропортящийся продукт. Каждая единица продукта имеет фиксированный срок жизни m. Уровень запаса отслеживается постоянно и уменьшается за счет удовлетворения спроса или избавления от устаревших единиц.
- 2) Заказ размером Q размещается, когда уровень запаса достигает точки перезаказа r. Существует положительное время доставки L для каждого пополнения и фиксированные затраты на оформление заказа K.
- 3) Все единицы заказа на пополнение запаса прибывают свежими или новыми. Полезность каждой единицы товара не уменьшается и не исчезает до момента окончания срока годности, но товар должен быть выброшен, если он не был использован до истечения срока хранения. Затраты, понесенные вследствие устаревания товара равны W за единицу.
- 4) Спрос в единицу времени, d1, – положительная случайная переменная. Предположим, что она имеет особое непрерывное или дискретное распределение с функцией плотности f1(y) = dPr{d1<=y}/dy и матожиданием D.
- 5) Единицы запаса всегда используются согласно FIFO политике выпуска (первый попавший на склад потребляется первым).
- 6) запас покидает систему либо для удовлетворения спроса, либо изымается как устаревший товар;
- 7) часть неудовлетворенного спроса в системе задалживается, а часть – теряется безвозвратно, причем, доля задолженного спроса не меняется в зависимости от продолжительности дефицита.
Для определения ожидаемого уровня запасов в системе необходимо знать ожидаемый уровень устаревших товаров и ожидаемый объем дефицита.
В качестве приближения ожидаемого количества устаревших товаров можно использовать соотношение (4):
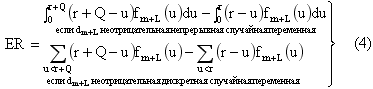
где r – точка заказа;
Q – размер заказа;
L – время доставки заказа;
Fm+L(u) – вероятностная функция случайной переменной dm+L (т.е. спрос в течение m+L единиц времени).
Для описания ожидаемого размера дефицита используется соотношение (5):
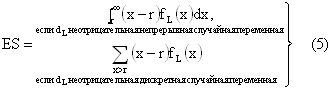
где функция fL(x) – это вероятностная функция случайной переменной dL – спроса во время поставки заказа.
Рассмотрим четыре приближения ожидаемого уровня запасов в единицу времени [9]:
- 1) грубая аппроксимация (без учета дефицита и устаревания товара);
- 2) аппроксимация Вагнера (без учета продолжительности дефицита и устаревания товара)[8].
- 3) модифицированный подход Вагнера (с учетом продолжительности дефицита, но исключающая устаревание товара).
- 4) приближение с учетом ожидаемого уровня устаревших товаров.
Аппроксимация Вагнера учитывает оба случая исчерпания и неисчерпания запаса во время доставки заказа и описывается соотношением (7):
Ожидаемый уровень запаса в единицу времени в модифицированной модели Вагнера можно выразить как:
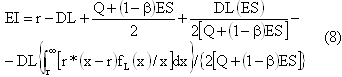
Аппроксимация с учетом устаревания товара описывает общий ожидаемый уровень запаса с помощью соотношения (9):
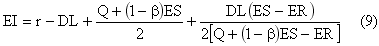
В [9] показано, что наилучшей моделью для описания уровня запаса в системе является модель с учетом дефицита и устаревания товара. Политика заказов (Q, r) может таким образом быть получена корректно, и отклонения в определении Q и r могут быть сведены к минимуму.
Оптимальная политика управления запасами, т.е. значения параметров Q и r, определяются из минимума общих затрат в единицу времени. Общие ожидаемые средние затраты в единицу времени для случая с частичным учетом неудовлетворенных требований можно определить из соотношения (10):
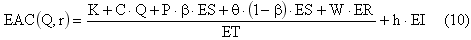
где ET – ожидаемая длина цикла, определяется из соотношения (11):
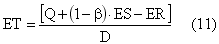
ER определяется из соотношения (3), ES – из соотношения (4).
В одном крайнем случае, когда b=0, случай с частичным учетом неудовлетворенных требований преобразуется в случай с полной потерей продаж, а в другом, когда b=1 – в случай с полным учетом неудовлетворенных требований.
1.4. Скидка на продажную цену товара для системы с периодическими проверками уровня запаса
1.4.1. Система с точным ожидаемым уровнем запаса
Чтобы уменьшить объем устаревших запасов, которые подлежат списанию, в [11, 12] предлагается ввести скидку на продажную цену продукции с целью повышения спроса, а, следовательно, уменьшения объема продукции, подлежащей списанию. Алгоритм определения скидки, описанный в [11, 12], определяет оптимальный размер заказа и оптимальную ценовую политику для системы с периодическим контролем уровня запаса. В такой системе периодически (раз в день, неделю, месяц) проверяется наличный запас и, если он опустился ниже заданного уровня, делается заказ на Q единиц.
Рассматривается только один вариант скидки, при этом предполагается, что спрос известен как для случая, когда скидка используется, так и для случая продаж по обычной цене.
Целью задачи является определение оптимального размера заказа и времени введения скидки. Оптимальный объем заказа выбирается из диапазона от 0 до заказа, который в сумме с остатком на начало периода давал бы максимальный запас.
Поиск оптимальных параметров представляет собой задачу динамической оптимизации. Функция цели состоит в том, чтобы максимизировать общий ожидаемый выигрыш, Qt(st (a, yt)), для состояния st полученный за время от текущего состояния t до конца горизонта планирования, и зависящий от решения принятого в отношении ценовой политики, a, и объема заказа yt. Параметр a принимает значение p или n, в зависимости от того, вводится скидка или нет. Выигрыш, r(st (a, yt)), определяется как разница между доходом и затратами. Затраты включают:
- затраты на хранение запаса,
- затраты, понесенные вследствие дефицита;
- затраты на оформление и приобретение заказа;
- затраты, возникающие в связи с устареванием товара;
- затраты на введение ценовой скидки.
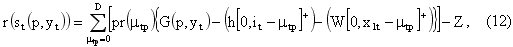
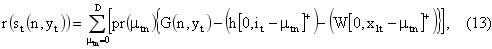
где mta – случайная переменная спроса в периоде t с известным распределением;
pr(mta) – вероятность того, что спрос в периоде t, при ценовой политике a будет равен mta;
it – общий запас в наличии в начале периода t;
xit – количество запасов в периоде t с оставшимся сроком использования i;
G(a, yt) определяется из соотношения (14):
где Ra – продажная цена;
[a, b]+ – максимум из (a, b), [a, b]– – минимум из (a,b).
В случае, если на этапе t было принято решение о введении ценовой скидки, то на всех последующих этапах рассчитывается только формула (12).
На последнем этапе затраты на содержание запаса отсутствуют, поэтому, ожидаемый выигрыш для случаев со скидкой и без определяется из соотношений (15) и (16) соответственно:
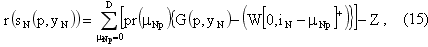
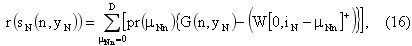
Общий ожидаемый выигрыш определяется по схеме (17):
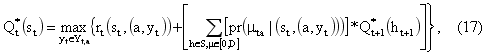
где Yt = {0…I – jt} – набор возможных значений для yt, I определяет максимальный запас, а jt – начальный запас, который переносится из предыдущего периода;
ht+1 – результирующее состояние в периоде (t+1);
pr (mta | (st, (a, yt))) – вероятность спроса mta в случае реализации действия (a, yt) в состоянии st в периоде t.
Оптимальная политика находится с помощью рекурсивной динамической процедуры, начиная с t = N и решая уравнение (12) пока t не станет равным нулю [1].
1.4.2 Система с приближенным ожидаемым уровнем запаса
Основной недостаток рассмотренного выше подхода заключается в том, что по мере роста срока годности скоропортящегося товара увеличивается возможное число состояний системы. Уменьшение числа состояний возможно благодаря суммированию количества некоторых запасов без существенной потери информации. В [9] предлагается аппроксимация, предполагающая группировку более свежих товаров.
Таким образом вектор запасов принимает вид:
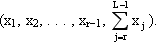
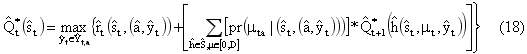
Где
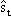 – вектор запасов.
– вектор запасов.
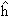 –
функция перехода, описывается формулами (19) и(20):
–
функция перехода, описывается формулами (19) и(20):
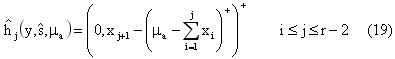
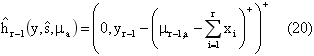
Рассмотренные в предыдущем разделе алгоритмы определения скидки не подходят для разрабатываемой системы в силу следующих причин:
- 1) В данных системах скидка выступает, скорее как второй вариант цены, поскольку оптимальные параметры политики управления запасами переопределяются каждый раз, когда мы выбираем новую цену. В разрабатываемой системе скидка должна быть инструментом, позволяющим в случае нестабильного спроса уменьшить остатки нераспроданного товара к окончанию его срока годности.
- 2) Предлагается только два варианта цены (со скидкой и без). На практике менеджер должен иметь больше вариантов ценовых скидок для более гибким управлением запасами.
- 3) Алгоритм имеет достаточно большую вычислительную сложность. Предложенная аппроксимация действует только для товаров с относительно небольшим скоком годности.
Рассмотрим основные условия использования скидки в рассматриваемой системе управления запасами скоропортящихся товаров:
- 1) Для управления запасами используется (Q, r)-система. Эта система характеризуется постоянным объемом заказа.
- 2) Для определения оптимальных параметров политики используются приближенные подходы.
- 3) Скидка может быть установлена не на всем интервале срока годности товара (0…m), а только за определенное количество дней, М, до окончания срока использования товара.
- 4) Скидка устанавливается только в том случае, если за M дней до окончания срока годности товара, Tm, его объем на складе превышает ожидаемый объем продаж в течение M дней при текущем спросе. Действие такой скидки можно увидеть на рисунке 4.
- 5) Оптимальный размер заказа не зависит от устанавливаемой скидки.
- 6) Кроме определения времени установления скидки, система предусматривает определения ее величины. Оптимизация проводится по нескольким заранее установленным значениям скидок (например, p1 = 5%, p2 = 10%, p3 = 15%, p4 = 20%, …).
- 7) Спрос на товар при различных значениях скидки известен.
Также, важно отметить, что целью введения скидки является не уменьшение объема списываемых в связи с устареванием товара запасов, а максимизация прибыли от реализации товара. Поэтому мы выбираем на ту скидку, при которой будет распродан весь товар, а ту, которая обеспечит максимальную выгоду. Это приводит к возникновению случаев, когда не весь объем товара будет реализован по истечении срока годности, а только его часть.
Ситуации с полной и частичной реализацией товара благодаря введению скидки изображены на рисунке 4.
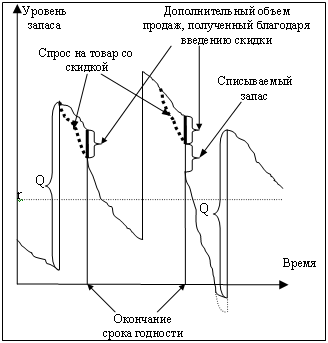
Алгоритм работы системы можно представить следующим образом:
Шаг 1. Определяется оптимальный размер заказа и точка заказа исходя из приближенных формул. Оптимальный размер заказа находится исходя из минимума средних ожидаемых издержек в единицу времени, определяемых соотношением (11).
Шаг 2. Пока (Tm – t) > M, , каждый раз, когда уровень запаса в системе опускается до r, производится заказ, объемом Q. Товар продается по обычной цене.
Шаг 3. При (Tm – t) <= M, то выполняется сравнение наличного запаса, Ut, и D(Tm – t) – ожидаемого объема реализации товара за время (Tm – t):
– если Ut <= D(Tm – t)
скидка не предлагается, возвращаемся к шагу 2;
– если Ut > D(Tm – t),
необходимо определить размер скидки, переходим к шагу 4.
Шаг 4. Полагаем i = Tm.
Прибыль за период времени (Tm – t), R(p, i), полученная при установлении скидки p = {p1, p2,…pn} определяется соотношением (21):
где D(p, i) – спрос товар со скидкой p за период времени i;
TCU – определяется соотношением (3) с учетом нового значения спроса.
Пока i не станет равным t определяем ожидаемую прибыль за период от t до Tm по формуле (22):
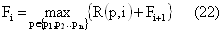
Fi+1 – оптимальное решение на предыдущем этапе. FTm+1 = 0.
Шаг 5. До истечения срока годности товар продается со скидкой, установленной на шаге 3.
Поскольку в рассмотренном алгоритме параметры оптимальной политики управления запасами определяются исходя из приближенных формул, а следовательно, более просты в расчетах, то использование данного алгоритма возможно и для более сложных многономенклатурных задач. Поскольку механизм определения скидки включается только за определенное время M до окончания срока годности товара, это позволяет максимально снизить вычислительную сложность алгоритма, в отличие от подхода рассмотренного в [9].
Данная система еще не может быть использована на практике, так как в ней рассматривается только один продукт. Реальные системы управления запасами должны быть многономенклатурными. Поэтому в рамках выпускной работы магистра планируется добавить в систему механизмы решения следующих задач:
- 1) классификация засов и выбор отдельных методов управления для различных товарных групп;
- 2) учет ограничения на вместимость склада;
- 3) учет ограничения на ограниченность денежных средств, вкладываемых в управление запасами;
- 3) разработка алгоритма оптимального распределения заказов во времени.
В данной работе быта рассмотрена (Q, r)-система управления скоропортящимся товарами. Разрабатываемая система основана на приближенном описании ее ожидаемых параметров.
Однако, в связи со случайным характером спроса, определение ожидаемого уровня запаса в системе и затем, оптимальных параметров системы (размера заказа и точки заказа) будет неточным. Тогда возможна ситуация, когда на складе остается нераспроданный товар с истекшим сроком годности и подлежащий списанию. В такой ситуации предприятие будет неизбежно нести убытки, определяемые стоимостью просроченных товаров и затратами на их списание.
Чтобы уменьшить такие убытки в разрабатываемой системе вводится скидка на продажную цену продукции. Возросший в результате снижения цены спрос, будет поглощать излишек запасов и уменьшит объем списываемой продукции. Кроме того, в зависимости от объема излишков, возможен выбор оптимального размера скидки, а также времени ее внедрения.
Для использования рассмотренной системы на практике в ней необходимо учесть также ограничения, возникающие при решении реальных многономенклатурных задач.
- www.cs.comizdat.com. Черненко М. Проблемы управления украинскими предприятиями. // Корпоративные системы, 2002, № 4.
- Бланк И.А. Основы финансового менеджмента в 2-х томах, т. 1. – М., Ника-Центр, 2000
- www.business.ua. Сергей Семенов. “Что там у него в карманцах?” // Бизнес, №18 (537), 05.05. 2003.
- Хедли Дж., Уайтин Т. Анализ систем управления запасами. – М., «Наука», 1969. – 511 с.
- Рыжиков Ю. И. Теория очередей и управление запасами: Учебное пособие для вузов. – СПб.: Питер, 2001. – 384 с.
- Хруцкий Е. А. Оптимизация хозяйственных связуй и материальных запасов (Вопросы методологии). – М.: Экономика, 1997. – 263 с.
- Букан Дж., Кенигсберг Э. Научное управление запасами. – М.: Наука, 1967. – 423 с.
- www.maths.ex.ac.uk/~DKSmith/Research.html David K. Smith. Dynamic Programming and Inventory Management: What Has Been Learnt in the Last Generation? //School of Mathematical Sciences University of Exeter, Exeter EX4 4QE, UK, 2000.
- www.edpsciences.org/articles/ro/pdf/1999/01/ro3.pdf Huan Neng Chiu, “A Good Approximation of the Inventory Level in a (Q r) Perishable Inventory System”, Operations Research, vol. 33, №1, 1999, pp. 29-45.
- Bwww.biostat.umn.edu/~tweedie/documents/invent.pdf W.L. Coopery and R.L. Tweediez, “Perfect Simulation of an Inventory Model for Perishable Products”, University of Minnesota, July 15, 2000.
- www.iitb.ac.in/~ieor/nh/Revised- chande_paper.pdfA Chande, N Hemachandra and N Rangaraj. Fixed-life perishable inventory problem and approximation under price promotion // Technical Report, Industrial Engineering and Operations Research, Indian Institute of Technology Bombay, Mumbai, 2004.
- www.ias.ac.in/sadhana/Pdf2005AprJun/Pe1304.pdf A Chandec, S Dhekane, N Hemachandra, N Rangaraj. Perishable inventory management and dynamic pricing using RFID technology // Industrial Engineering and Operations Research, Indian Institute of Technology, Bombay, Mumbai, Sadhana Vol. 30, Parts 2 & 3, April/June 2005, pp. 445–462.
* При написании данного реферата, магистерская работа еще не завершена. Окончательное завершение: январь 2007 года. Полный текст работы и все материалы по теме могут быть получены у автора или его руководителя после указанной даты.