Статистические методы прогнозирования
|
|
Источник:
Четыркин Е.М. Статистические методы прогнозирования - М.: Статистика, 1977.- 199с. |
|
Когда регрессия специфицирована и оценены ее параметры, она может быть применена для прогнозирования. Уравнение регрессии характеризует взаимосвязь между переменными x и y. Однако в самом уравнении регрессии с оцененными параметрами нет указания на то, как близко находятся фактические наблюдения от расчетных, иначе говоря, нет указания на степень тесноты связи между переменными. Поэтому оценка параметров регрессии обычно сопровождается расчетом такой дополнительной характеристики, как коэффициент корреляции, который представляет собой эмпирическую меру линейной зависимости между x и y. Продолжим говорить о линейной парной регрессии. Коэффициент корреляции для некоторой выборки значений x и y определяется по формуле |
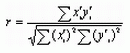
|
|
Величина r лежит между -1 и 1. чем выше значение r , тем теснее связь между переменными и тем с большим основанием найденная взаимосвязь может быть использована для прогнозирования. Коэффициент корреляции также может рассматриваться как один из критериев качества подбора функции. После получения r можно продолжить статистический анализ, исследовав вопрос, в какой мере полученный коэффициент корреляции существенен (т.е. существенно ли r отличается от нуля или его отличие от нуля можно приписать влиянию случайности, связанной с выборкой). Для проверки существенности при небольшом числе наблюдений применяют формулу |
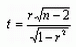
|
|
Величина t здесь следует t-распределению Стьюдента,
поэтому найденное значение t можно сопоставить с табличным
значением
Итак, мы оценили параметры a и b и получили регрессию,
на основе которой можно предсказывать значения y в
зависимости от значений x . Естественно полагать, что действительные
значения зависимой переменной не будут совпадать с расчетными
(прогнозными), так как сама линия регрессии описывает взаимосвязь
лишь в среднем, в общем. Отдельные наблюдения рассеяны вокруг нее.
Таким образом, первым и наиболее очевидным фактором, во многом
определяющим надежность получаемых по уравнению регрессии
прогностических оценок, является рассеяние наблюдений вокруг
линии регрессии. В качестве меры рассеяния примем такую
общераспространенную характеристику, как дисперсия.
Для ее определения найдем сумму квадратов отклонений фактических
отклонений от линии регрессии с параметрами a и b , т.е.
Вычислим |
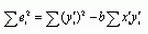
|
|
Значение величины
|
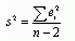
|
|
Величина
Рассмотрим теперь метод определения доверительных границ
для значения
Таким образом, дисперсия значения зависимой переменной,
определяемой по уравнению парной линейной регрессии будет
складываться из двух компонент - дисперсии параметра a и дисперсии параметра b.
Эти дисперсии соответственно равны
|
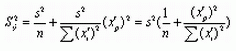
|
|
где
Зная дисперсию показателя
|
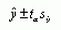
|
|
где
Эти доверительные границы расположатся выше и ниже линии регрессии
в виде ветвей гиперболы, ограничивая доверительную зону.
Эта доверительная зона определяет местоположение линии регрессии
(т.е. средних величин
Таким образом, уравнению
|
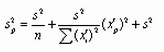 или
или

|
|
Доверительные интервалы для прогнозов индивидуальных значений
|
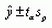
|
|
Таким образом,когда регрессия специфицирована и оценены ее параметры, она может быть применена для прогнозирования. Очевидно, что точность прогноза определяется не только точностью самого уравнения регрессии, но и тем, насколько надежно оценены будущие значения независимых переменных. |
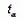 при n-2 степенях свободы.
при n-2 степенях свободы.
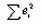
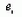 :
:
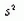 является выборочной оценкой дисперсии случайных членов
является выборочной оценкой дисперсии случайных членов
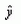 т.е. тех границ, в пределах которых с заданной доверительной
вероятностью будет находиться значение
т.е. тех границ, в пределах которых с заданной доверительной
вероятностью будет находиться значение
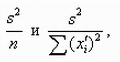 ,
откуда
,
откуда
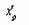 - значение переменной x (выраженное в виде отклонения от средней),
для которого определяется
- значение переменной x (выраженное в виде отклонения от средней),
для которого определяется
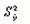 имеет минимальное значение в точке
имеет минимальное значение в точке
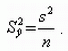 .
.
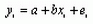 соответствует дисперсия
соответствует дисперсия
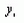 будут, следовательно, равны:
будут, следовательно, равны: