Назад в библиотеку
Исходный URL : http://www.omsu.omskreg.ru/vestnik/articles/y1999-i2/a017/article.html
РЕШЕНИЕ ЗАДАЧИ РАЗМЕЩЕНИЯ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ С ЗАПРЕЩЕННОЙ ОБЛАСТЬЮ
Г.Г. Забудский, И.В. Нежинский
Институт информационных технологий и прикладной математики СО РАН,
644099 Омск , ул. Певцова 13
| In this paper we consider a special case of well-known Fermat-Weberproblem. The problem is to locate the object in the complement of some sphere in Euclidean space. It is problem of nonconvex optimization. We propose algorithm for solving of the problem. It is modification of the algorithm A.S. Strekalovsky. |
1. Постановка задачи
Задачи размещения объектов часто возникают на практике и издавна привлекают
к себе внимание специалистов [1-3,5,7,8].
Впервые одну из таких задач поставил Ферма в XVII веке. Она заключалась
в поиске такой точки на плоскости, сумма
расстояний от которой до трех заданных точек была минимальна. В дальнейшем
рассматривались задачи размещения в произвольном конечномерном пространстве.
Требовалось разместить несколько объектов относительно некоторого числа
фиксированных объектов с произвольными положительными
удельными стоимостями связей.
Такой класс задач часто называют задачами Вебера или Штейнера-Вебера [5].
Алгоритмы решения этих задач зависят от метрики, выбираемой для
определения расстояний между объектами.
Если метрика прямоугольная,
то задача сводится к специальной задаче линейного программирования, в частности,
к решению серии задач отыскания максимального потока [5, 7].
В случае евклидовой метрики задача относится к классу задач
выпуклого программирования. Мы будем рассматривать задачу размещения
одного объекта в евклидовом пространстве вне некоторой запрещенной области.
Объект имеет произвольные положительные стоимости связей с
фиксированными объектами.
Пусть в евклидовом пространстве Rn зафиксированно m объектов, координаты
которых обозначим через  .
Задана также запрещенная область - сфера с центром в точке B, радиуса r.
Через ci обозначим удельные стоимости связей между размещаемым и
фиксированными объектами. Необходимо так разместить объект в допустимой
области, чтобы суммарная стоимость связей была минимальной. Математическая модель
задачи имеет вид.
.
Задана также запрещенная область - сфера с центром в точке B, радиуса r.
Через ci обозначим удельные стоимости связей между размещаемым и
фиксированными объектами. Необходимо так разместить объект в допустимой
области, чтобы суммарная стоимость связей была минимальной. Математическая модель
задачи имеет вид.
 |
|
|
(1) |
 |
|
|
(2) |
где

Постановка задачи размещения (1) - (2) нам не встречалась в литературе
и, по-видимому, ранее не рассматривалась.
Задача (1) - (2) не относится к классу задач выпуклой оптимизации,
для которого разработано достаточное количество эффективных алгоритмов. Наличие
ограничения (2) делает задачу многоэкстремальной.
Отметим, что даже
при решении задачи без ограничения градиентными алгоритмами возникают
проблемы "особых" точек, в которых не определен
градиент целевой функции. Решению задачи (1) посвящены, например, работы
[1, 8]. В них приводятся алгоритмы нахождения оптимального решения,
основанные на решении системы нелинейных уравнений.
Решению многоэкстремальных задач, в частности, специальных классов,
в последнее время уделяется много внимания [6, 9, 10]. Алгоритм решения задач,
в которых целевая функция выпукла, а допустимая область является дополнением
выпуклого
множества, приведен в работах А.С. Стрекаловского [6, 10]. Нами реализован
алгоритм решения задачи (1) - (2), основанный
на указанном подходе с учетом специфики задачи. Проведены
вычислительные эксперименты, которые показали его эффективность.
2. Алгоритм решения задачи
В дальнейшем будем предполагать, что все фиксированные объекты не лежат
на одной прямой. В этом случае
целевая функция строго выпукла[8]. Будем также считать, что выполнено следующее
предположение: оптимальное
решение задачи (1) не совпадает с оптимальным решением задачи (1) - (2).
Это условие будем обозначать (*).
Класс задач со свойством (*), у которых целевая функция выпукла, а
допустимая область является дополнением выпуклого множества,
получил название обратно-выпуклых задач [6, 10]. Сложность решения
этих задач
состоит в том, что они являются многоэкстремальными. Поэтому после
нахождении какого-либо
экстремума необходимо иметь способ определения: является ли полученная
точка локальным или глобальным экстремумом. В случае локального экстремума
необходимо найти способ перехода в другой локальный минимум с лучшим значением целевой
функции. Существует несколько методов решения многоэкстремальных задач.
Практически все они не гарантируют нахождение глобального экстремума. К таким методам
относятся: метод "тяжелого шарика", перебор локальных экстремумов с помощью
рассмотрения различных начальных точек , метод "спуск-подъем-перевал",
методы покрытий и др.
Проблема состоит в том, что нет достаточных условий глобального экстремума.
Вероятно, одним из первых, кто предложил такие достаточные условия для
специального класса задач, был А.С. Стрекаловский.
В его работе [6] рассматривалась следующая задача

где  ,
где S - выпуклое
множество, а f(x), g(x) - выпуклые функции. Кроме того,
для задачи (P) выполнено предположение (*). Нетрудно заметить, что в этом случае
решение z задачи (P) находится на границе допустимой области, т.е. удовлетворяет условиям
g(z)=0.
Обоснованием алгоритма решения подобных задач служит следующая теорема.
,
где S - выпуклое
множество, а f(x), g(x) - выпуклые функции. Кроме того,
для задачи (P) выполнено предположение (*). Нетрудно заметить, что в этом случае
решение z задачи (P) находится на границе допустимой области, т.е. удовлетворяет условиям
g(z)=0.
Обоснованием алгоритма решения подобных задач служит следующая теорема.
Теорема [6]. Для того чтобы точка z являлась
решением задачи (P), необходимо и достаточно, чтобы выполнялись
условия
Таким образом, чтобы проверить является ли z глобальным экстремумом,
необходимо решить следующую задачу:
Если  для всех
для всех  ,
то z глобальный минимум
в задаче (P). Так как невозможно перебрать все точки границы
допустимой области, то в работе [6] предложена ее дискретная аппроксимация,
которая назвывается R-множеством. Для решения задачи(P')
предлагается декомпозиционный алгоритм. Декомпозиция заключается
в разбиении исходной задачи на две:
нахождении x при фиксированном y, после чего с полученным
значением x решается задача по переменной y.
,
то z глобальный минимум
в задаче (P). Так как невозможно перебрать все точки границы
допустимой области, то в работе [6] предложена ее дискретная аппроксимация,
которая назвывается R-множеством. Для решения задачи(P')
предлагается декомпозиционный алгоритм. Декомпозиция заключается
в разбиении исходной задачи на две:
нахождении x при фиксированном y, после чего с полученным
значением x решается задача по переменной y.
Опишем по шагам алгоритм решения задачи (1) -(2), основанный на
изложенной выше схеме с учетом специфики задачи.
Алгоритм решения задачи (1) - (2):
Шаг 1. Методом проекции градиента, начиная с  ,
находим локальный минимум задачи. Пусть zk точка, найденная на этом шаге.
,
находим локальный минимум задачи. Пусть zk точка, найденная на этом шаге.
Шаг 2. Строим R-множество следующим образом:
Шаг 3. Для каждого  решаем задачу методом возможных
направлений [4]
решаем задачу методом возможных
направлений [4]
где 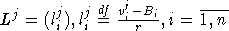
Шаг 4. Пусть  ,
решение задачи на шаге 3. Для каждого
xj решаем задачу
,
решение задачи на шаге 3. Для каждого
xj решаем задачу
где  и
и 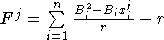 .
Алгоритм решения этой задачи приведен в Замечании 1.
Пусть
.
Алгоритм решения этой задачи приведен в Замечании 1.
Пусть  решения, полученные на этом шаге.
решения, полученные на этом шаге.
Шаг 5. Найдем  .
Предположим, что максимум достигается в точке xt.
.
Предположим, что максимум достигается в точке xt.
Шаг 6. Если  ,
тогда полагаем uk+1:=xt и возвращаемся на Шаг 1.
,
тогда полагаем uk+1:=xt и возвращаемся на Шаг 1.
Шаг 7. Если  ,
тогда Стоп. Точка zk - глобальный оптимум.
,
тогда Стоп. Точка zk - глобальный оптимум.
Замечание 1. Задачу на шаге 4 можно решить аналитически следующим образом. В силу того, что
допустимое множество сфера, а целевая функция линейна, то ее максимум будет
достигаться в точке, которая лежит на сфере и в которой гиперплоскость с
нормалью целевой функции касается сферы с подходящим значением свободного члена.
Точками касания сферы и гиперплоскости будут
 .
Выбрав ту из них, в которой
.
Выбрав ту из них, в которой  ,
получим решение задачи.
,
получим решение задачи.
Замечание 2. На шаге 1 проблема "особых" точек решалась способом, предложенным в
работе [8].
3. Результаты экспериментов
Вычислительные эксперименты проводились для решения задач на плоскости
и в пространстве размерности до 20. Количество фиксированных объектов
варьировалось
от 3 до 150. В задачах на плоскости исходные данные подбирались случайно и некоторым
специальным образом. Начальная точка выбиралась в окрестности локального экстремума,
не являющегося глобальным.
Разрешающее множество
в задачах размерности не более 10 выбиралось, как и описано в алгоритме. В
задачах большей размерности, с учетом большого количества точек, брались не
все симметричные точки, а лишь те, для которых выполнено неравество
 .
.
В результате проведенных экспериментов выяснилось, что независимо от того,
каким образом выбиралась начальная точка (произвольно или в окрестности
локального экстремума) за одну, максимум за
две итерации, алгоритм находил решение задачи (1) - (2)
в задачах на плоскости.
После такого же количества итераций алгоритм останавливался и для задач
большей размерности.
В этом случае нет гарантии нахождения глобального экстремума, так как это
зависит
от "плотности" R - множества. В таких задачах для большей уверенности в
нахождении решения задачи выбиралось несколько начальных точек.
Кроме того,
эксперименты показали, что при больших значениях радиуса запрещенной
сферы задача имеет один экстремум.
Замечание 3. Пусть допустимая область задачи состоит из дополнения к
k непересекающимся сферам, с центрами и радиусами
 соответственно. Тогда решение такой задачи сводится к
решению задачи (1) - (2). Действительно, пусть
соответственно. Тогда решение такой задачи сводится к
решению задачи (1) - (2). Действительно, пусть  минимум функции
(1) на всем пространствеRn. Если
минимум функции
(1) на всем пространствеRn. Если  для всех
для всех
 ,
то, очевидно,
,
то, очевидно,  оптимальное решение исходной
задачи. Если существует номер j (не более одного по условию), такой что
оптимальное решение исходной
задачи. Если существует номер j (не более одного по условию), такой что
 ,
то решение исходной задачи находится на сфере
j. Полагая B=Bj, r=rj, решаем задачу (1) - (2) и получаем решение
исходной задачи.
,
то решение исходной задачи находится на сфере
j. Полагая B=Bj, r=rj, решаем задачу (1) - (2) и получаем решение
исходной задачи.
Аналогично рассматривается случай, когда размещается
несколько объектов (более одного), не связанных между собой. Исходная задача
декомпозируется на независимые подзадачи, т. е. для каждого объекта поочередно
решается задача (1) - (2).
Работа выполнена при финансовой поддержке
РФФИ (код проекта 97-01-00771).
Литература
| [1] |
Аоки М. Введение в методы оптимизации// М.: Наука, 1977. 344 с.
|
| [2] |
Забудский Г.Г. Алгоритм решения одной задачи оптимального линейного упорядоченения
//Известия вузов. Математика. 1997. N 12. С. 73 -78.
|
| [3] |
Забудский Г.Г. Некоторые свойства многогранника задачи о p -медиане
//Вестник Омского университета. 1997. N 4. С. 11 -13.
|
| [4] |
Зуховицкий С.И. , Авдеева А.И. Линейное и выпуклое программирование. М.: Наука, 1967.
460 с.
|
| [5] |
Исследования операций. Модели и применения. М.: Мир, 1981. Т. 2. 344 с.
|
| [6] |
Стрекаловский А.С. К проблеме глобального экстремума в невыпуклых задачах оптимизации
//Известия вузов. Математика. 1990. N 8. С. 74 -80.
|
| [7] |
Трубин В. А. Эффективный алгоритм для задачи Вебера с прямоугольной метрикой
// Кибернетика. 1978. N 6. С. 67-70.
|
| [8] |
H. W. Kurn. A note on Fermat's problem// Mathematical
Programming 4.-North-Holland Publishing Company, 1973. P. 98 - 107.
|
| [9] |
J.-B Hiriart-Urruty. From convex optimization to non-convex optimization.
Part 1: Necessary and sufficient conditions for global optimality in
Nonsmooth and Related Topics, Plenum Press. P. 219 - 239.
|
| [10] |
A. Strekalovsky, Ider Tsevendorj. Testing the R-algorithm for reverse convex
problem// 916. Новосибирск: ВЦ СО АН СССР, 1990.
32с.
|
 .
Задана также запрещенная область - сфера с центром в точке B, радиуса r.
Через ci обозначим удельные стоимости связей между размещаемым и
фиксированными объектами. Необходимо так разместить объект в допустимой
области, чтобы суммарная стоимость связей была минимальной. Математическая модель
задачи имеет вид.
.
Задана также запрещенная область - сфера с центром в точке B, радиуса r.
Через ci обозначим удельные стоимости связей между размещаемым и
фиксированными объектами. Необходимо так разместить объект в допустимой
области, чтобы суммарная стоимость связей была минимальной. Математическая модель
задачи имеет вид.




 ,
где S - выпуклое
множество, а f(x), g(x) - выпуклые функции. Кроме того,
для задачи (P) выполнено предположение (*). Нетрудно заметить, что в этом случае
решение z задачи (P) находится на границе допустимой области, т.е. удовлетворяет условиям
g(z)=0.
Обоснованием алгоритма решения подобных задач служит следующая теорема.
,
где S - выпуклое
множество, а f(x), g(x) - выпуклые функции. Кроме того,
для задачи (P) выполнено предположение (*). Нетрудно заметить, что в этом случае
решение z задачи (P) находится на границе допустимой области, т.е. удовлетворяет условиям
g(z)=0.
Обоснованием алгоритма решения подобных задач служит следующая теорема.


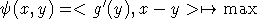

 для всех
для всех  ,
то z глобальный минимум
в задаче (P). Так как невозможно перебрать все точки границы
допустимой области, то в работе [6] предложена ее дискретная аппроксимация,
которая назвывается R-множеством. Для решения задачи(P')
предлагается декомпозиционный алгоритм. Декомпозиция заключается
в разбиении исходной задачи на две:
нахождении x при фиксированном y, после чего с полученным
значением x решается задача по переменной y.
,
то z глобальный минимум
в задаче (P). Так как невозможно перебрать все точки границы
допустимой области, то в работе [6] предложена ее дискретная аппроксимация,
которая назвывается R-множеством. Для решения задачи(P')
предлагается декомпозиционный алгоритм. Декомпозиция заключается
в разбиении исходной задачи на две:
нахождении x при фиксированном y, после чего с полученным
значением x решается задача по переменной y.
 ,
находим локальный минимум задачи. Пусть zk точка, найденная на этом шаге.
,
находим локальный минимум задачи. Пусть zk точка, найденная на этом шаге.


 решаем задачу методом возможных
направлений [
решаем задачу методом возможных
направлений [

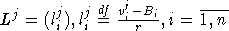
 ,
решение задачи на шаге 3. Для каждого
xj решаем задачу
,
решение задачи на шаге 3. Для каждого
xj решаем задачу

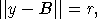
 и
и 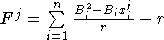 .
Алгоритм решения этой задачи приведен в Замечании 1.
Пусть
.
Алгоритм решения этой задачи приведен в Замечании 1.
Пусть  решения, полученные на этом шаге.
решения, полученные на этом шаге.
 .
Предположим, что максимум достигается в точке xt.
.
Предположим, что максимум достигается в точке xt.
 ,
тогда полагаем uk+1:=xt и возвращаемся на Шаг 1.
,
тогда полагаем uk+1:=xt и возвращаемся на Шаг 1.
 ,
тогда Стоп. Точка zk - глобальный оптимум.
,
тогда Стоп. Точка zk - глобальный оптимум.
 .
Выбрав ту из них, в которой
.
Выбрав ту из них, в которой  ,
получим решение задачи.
,
получим решение задачи.
 .
.
 соответственно. Тогда решение такой задачи сводится к
решению задачи (1) - (2). Действительно, пусть
соответственно. Тогда решение такой задачи сводится к
решению задачи (1) - (2). Действительно, пусть  минимум функции
(1) на всем пространствеRn. Если
минимум функции
(1) на всем пространствеRn. Если  для всех
для всех
 ,
то, очевидно,
,
то, очевидно,  ,
то решение исходной задачи находится на сфере
j. Полагая B=Bj, r=rj, решаем задачу (1) - (2) и получаем решение
исходной задачи.
,
то решение исходной задачи находится на сфере
j. Полагая B=Bj, r=rj, решаем задачу (1) - (2) и получаем решение
исходной задачи.