1.2. РАСПРОСТРАНЕНИЕ ВОЛНЫ ИЗЛУЧЕНИЯ В РЕАЛЬНОЙ СРЕДЕ

 

Выясним, к каким изменениям решения уравнений Максвелла приведет учет неидеальностей, имеющих место в реальных условиях распространения световых волн. Прежде всего очень часто приходится учитывать то, что оптическая среда небезгранична. Типичные примеры этого – распространение излучения по волоконно-оптическим световодам, имеющим цилиндрическую симметрию, или по плоским интегрально-оптическим диэлектрическим волноводам. В обоих случаях поперечные размеры оптических сред соизмеримы с длиной волны света l, протяженность же среды вдоль направления распространения можно считать бесконечной. Другой пример – распространение световой волны внутри лазера. Здесь необходимо учитывать наличие границ по всем трем координатам, т. е. мы встречаемся с задачей возбуждения объемного резонатора.

Рассмотрим однородный бесконечно протяженный волновод (рис. 1.4), у которого обозначим через S контур, ограничивающий это сечение. Решать уравнения Максвелла удобно, пользуясь поляризационным потенциалом (или вектором Герца) Пг, связанным с вектором-потенциалом А [см. формулу (1.6)] простым соотношением

 

                                            (1.18)

 

Если положить, что поля в волноводе меняются по периодическому закону ехр(–iwt), омических потерь нет (s = 0) и вектор Пг имеет лишь один компонент

направленный вдоль оси z, то решение может быть представлено в виде

Пг(М ,z,t) = y(М) f(z) ехр (-iwt),     (1.19)

где М – произвольная точка, лежащая в поперечном сечении s, имеющая координаты х и у; y(М) –собственная функция задачи о колебаниях мембраны, закрепленной по контуру, т. е.

 

D2y + a2y = 0;                                                 

yS = 0,                                                     (1.20)

имеющей бесконечную систему собственных значений {а2m} и собственных функций {ym}. Частные решения z-составляющей вектора Герца fm(z) определяются из уравнения

 

                                 (1.21)

 

Для волны, распространяющейся в положительном направлении оси z,

 

                              (1.22).

 

Общее решение уравнения Максвелла для волновода на рис. 1-4,а, представляющее собой суперпозицию всех частных решений, имеет вид:

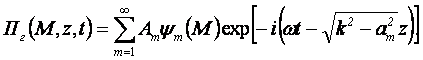                   (1.23).

 

Подобные выражения могут быть получены и для волн Пг(М, z, t), у которых имеется z-составляющая не электрического [как при выводе (1.23)], а магнитного вектора. В этом случае амплитуда волны представляет собой решение для колебаний мембраны, не закрепленной (свободной) по контуру S.

Итак, волна, распространяющаяся вдоль оси волновода (см. рис. 1.4,а) представляет собой дискретную совокупность плоских волн, амплитуды и фазы которых в каждой точке сечения s определяются решением задачи для колебание закрепленной (или свободной) мембраны, а волновые числа равны . Каждая из составляющих в (1.23) представляет тип волны, или вол-новую моду, характеризующуюся специфической структурой электромагнитного поля. Все моды волновода относятся к двум группам:

волны П(М, z, t), у которых Еz ¹ 0, Hz = 0, называемые электрическими. Е- или TМ-волнами;

волны Пг(М, z, t), у которых Еz = 0, Hz ¹ 0 (т. е. поле Е поляризовано в плоскости z = const), называемые магнитными Н- или ТE-волнами1.

Любое поле в волноводе представляет суперпозицию полей ТЕ и ТМ.

Уравнение (1.23) описывает незатухающие волны, распространяющиеся в направлении z, при условии k > аmmin. Таким образом, с учетом (1.15) для каждого волновода получаем критические значения частоты и длины волны

wкр = аmmin vф = аmmin с/n; lкр = 2p/аmmin.           (1.24)

По волноводу могут распространяться лишь волны с w ³ wкр и l £ lкр. Вследствие этого число распространяющихся мод всегда конечно, причем их тем больше, чем значительнее различие между частотой вводимого в волновод излучения w и критическим значением собственной частоты волновода wкр (или l и lкр).

Волновое число каждой составляющей в (1.23)    отсюда

               (1.25)

1 В аббревиатурах ТМ, ТЕ буква Т (от англ. transverse – поперечный)  означает, что ТМ и ТЕ – поперечные по Н и по Е волны.

Отсюда следует, что разные составляющие электромагнитной волны волновода имеют разные групповые скорости, при приближении к критическому режиму (l ® lкр) скорость распространения волны vг,в ® 0, а длина волны lв ® ¥, т. е. режим из волнового становится колебательным.

Проиллюстрируем общие положения на примерах. Для волновода  с сечением s и виде прямоугольника (b1 – толщина, b2 – ширина) собственные значения уравнения (1.20) зависят от двух целочисленных аргументов m и j:

 

                       (1.26)

 

Простейшая электрическая волна – ТМ11 (здесь m ¹ 0 и j ¹ 0, так как силовые линии магнитного поля не могут упираться в стенки и замыкаются сами на себя), а простейшая магнитная – ТЕ10. Структура этих волн (расположение силовых линий электрического и магнитного полей для фиксированного момента времени) представлена на рис. 1.4,б,в. Если принять b2 >> b1[ (что типично для интегрально-оптических волноводов), то, полагая в (1.26) m = 1, получаем, что при l ³ 2b1 в волноводе может существовать лишь одна мода ТЕ10.

Для круглого волновода радиуса r0 собственные значения

                                             (1.27)

где c(m)j – j-и корень уравнения Jm(c) = 0, где Jm – функция Бесселя m-го порядка. Поскольку c(0)1 = 2,4, то с учетом (1.24) получим условие существования лишь одной волны для круглого волновода: l ³ 2,6r0.

Наглядное представление о волновых модах дает лучевая теория (см. § 1.4), основанная на концепции зигзагообразного распространения света в волноводе. Соответственно этому каждая мода волнового поля представляет собой луч, падающий на границу волновод – окружающая среда под определенным углом q и распространяющийся по волноводу вследствие полного внутреннего отражения. Фактически тождественность волноводных мод и «косых» световых лучей вытекает и из решений уравнения Максвелла для волн П(М, z, t) и Пг(М, z, t). Действительно, дли всех мод, кроме ТЕ10, наряду с радиальными составляющими полей Е и Н имеются еще и осевые (вдоль оси z) хотя бы одного из этих полей. Геометрически это и означает плоскую волну, направление распространения которой отлично от z, причем это направление изменяется во времени (отражение от границ в лучевой теории). Несмотря на зигзагообразный путь такого луча свет (точнее, энергия излучения) распространяется лишь в направлении z (см. рис. 1.4), образуя в перпендикулярном направлении стоячую волну. Предельное значение угла падения, при котором могут существовать волноводные моды, определяется условием полного внутреннего отражения [см. формулу (1.36)] с заменой aп.в.о. на qп.в.о. Для некоторых лучей внутри этого угла выполняются такие фазовые соотношения, при которых многократно отраженные от различных границ плоские волны интерферируют в фазе, т. е. не подвергаются «самогашению». Именно эти лучи (или волны) представляют собой волноводные моды, прочие типы колебаний по мере распространения постепенно затухают. Волноводные моды определяются набором углов qm,j, (целочисленные аргументы m и j отражают дискретность q в направлениях х и у), представляющих собой частные решения трансцендентного уравнения, определяющего изменение фазы волны при распространении по волноводу. Итак, волноводные моды в лучевой теории тождественны световым лучам, направленным под углами qm,j к оси 0z, причем число разрешенных значений qm,j конечно.

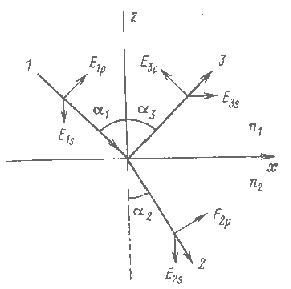
Другой практически важный случай отступления от идеализации (см. § 1.1) — это падение светового луча на границу раздела двух сред. Рассмотрим простейшую задачу. Пусть граница раздела двух изотропных полубесконечных сред с показателями преломления n1 и n2 представляет собой плоскость ху, на которую под углом a1 падает плоская электромагнитная волна (рис. 1.5). Уравнения Максвелла решаются по той же схеме, что и раньше, при этом граничные условия в плоскости ху выражаются в непрерывности тангенциальных составляющих векторов Е и Н. Решение приводит к появлению двух составляющих распространяющейся волны — преломленной (луч 2) и отраженной (луч 3). Существуют простые взаимосвязи направлений лучей 1, 2 и 3 (законы отражения и преломления):

 

a1 = a3;    n1×sina1 = n2 sin a2.                                  (1.28)

 

При этом все три луча лежат в одной плоскости – плоскости падения. Если разложить электрический вектор падающей волны на составляющие Е1р, лежащую в плоскости падения, и Е1s, перпендикулярную ей, то для аналогичных составляющих преломленной и отраженной волн решение уравнений Максвелла дает известные формулы Френеля1:

 

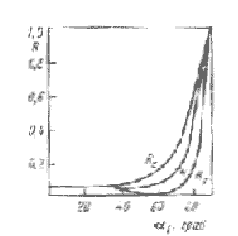
Рис. 1.5. Преломление и отражение света на границе двух сред	Рис.1.6. Зависимость коэффициента отражения R и его составляющих от угла падения для системы воздух-кварц (Rp соответствует поляризации света в плоскости р проходящей через лучи 1 и 3, Rs – поляризации света в плоскости s, проходящей через луч 3 и перпендикулярной плоскости р)

 

                                 

                                   (1.29)

                                              

                                                     

 

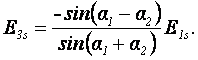
1 Интересно, что эти формулы получены за 40 лет до того, как были предложены уравнения электродинамики. Заложенная при их выводе неверная физически, но верная математически модель — поперечные колебания «эфира» — привела к правильным результатам.

Из анализа (1.28) и (1.29) можно сделать ряд важных выводов:

1. Фаза преломленной волны всегда совпадает с фазой падающей волны (Е2р и Elp, E2s и Els имеют одинаковые знаки при любых соотношениях a1 и a2); фазы составляющих отраженной волны могут отличаться от фаз таких же составляющих падающей волны на  0 ... p  в зависимости от угла падения.

2. Во всех экспериментах с отраженными и преломленными волнами измеряются их интенсивности, которые согласно (1-13) пропорциональны квадратам соответствующих амплитуд. Вводимые соответственно этому коэффициенты пропускания Т и отражения R (см. рис. 1.5).

 

                           (1.30)

 

для любого конкретного случая могут быть определены на основе формул Френеля. Дифференциальная форма этих параметров определяется как t=dI2/dI1 и r = dI3/dI1. Для неполяризованного (естественного) света получаем

 

                         (1.31)

 

Из расчетных зависимостей коэффициентов отражения от угла падения для разных случаев поляризации (рис. 1.6) видно, что до некоторого угла a1 величина  R  и  ее  составляющие почти постоянны, а затем резко возрастают до R = 1.

3. При нормальном падении луча света на границу раздела

 

R┴ = (n2 - n1)/(n2 + n1),                                     (1-32)

 

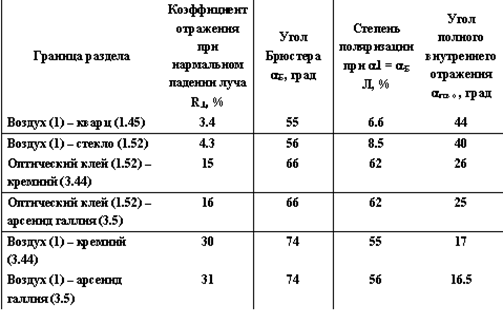
независимо от вида поляризации и от того, с какой стороны падает волна. Для некоторых практически важных в оптоэлектронике границ раздела значения  R┴ приведены в табл. 1.1. Коэффициент отражения изменяется от единиц до нескольких десятков процентов. Характерно, что и для лучей, отличных от нормального, но близких к нему (до a1 » aБ, где aБ — угол Брюстера, см. ниже), R » R┴. Из табл. 1.1 видно, в частности, что если между средами 1 и 2 поместить промежуточный слой с показателем преломления n1 < nnp < n2, то энергия отраженной волны уменьшится. Наиболее эффективно этот промежуточный просветляющий слой действует,

 

                                                        (1-33)

 

Таблица 1.1

Оптические характеристики некоторых границ раздела

4. Из (1.29) следует, что при (a1 + a2)®p/2  Е3p®0 и вектор Е3 совпадает с E3s, т. е. отраженный свет линейно поляризован в плоскости падения луча. Физически этот вывод, составляющий содержание закона Брюстера, основан на том, что поле волны 1, проникая во вторую среду, вызывает в ней колебания электронов, параллельные вектору Е2, и излучение ими вторичных волн в направлении, перпендикулярном их колебаниям. Вторичные волны и составляют отраженную волну 3. Понятно, что если угол между прошедшим 2 и отраженным 3 лучами составит p/2, то отраженный луч не будет содержать р-компонент. Условие  a1 + a2 = p/2  и определяет угол Брюстера

 

aБ = arctg(n2/n1).                                                         (1.34)

 

Степень   поляризации   естественного   света   при   выполнении   условия   a1 = aБ

 

                                        (1.35)

 

Из табл. 1.1 видно, что отражение от сред с большим показателем преломления может быть использовано для эффективной поляризации естественного света. Если рассчитанная по (1.35) степень поляризации недостаточна, применяют набор плоскопараллельных пластин, при этом Л приближается к 100%.

 5. Если на рис. 1.5 поменять направления лучей 2 и 1  (луч 2 станет падающим, а луч 1 — преломленным), то при условии

 

a2 = aп.в.о. ³ arcsin(n1/n2),                               (1.36)

 

наступает полное внутреннее отражение; энергия волны не переходит из среды 2 в среду 1. Детальное рассмотрение этого процесса показывает, что некоторое проникновение волны в среду 1 все же имеет место, но глубина этого проникновения (оцениваемая по уменьшению интенсивности в е раз), как правило, не превышает 0,5 l.

Из условия (1.36) aп.в.о. имеет действительные значения лишь при n2 > n1, т. е. при распространении света в оптически более плотной среде. При большом различии  n2 и n1  выйти из второй среды в первую могут лишь лучи, близкие к нормальным (см табл. 1.1).

Соотношения (1.28) – (1.36) широко используются в опто-электронике при расчете чувствительности фотоприемников, излучения светодиодов и лазеров, распространения волн по двухслойным оптическим волокнам, при изготовлении поляризаторов и модуляторов света.

Вернемся к рассмотрению безграничной изотропной среды, но учтем, что реально s ¹ 0. В этом случае в отличие от (1.7) получим

                        (1.37)

где, как и прежде, под u подразумеваются j, А, Е, Н или любая их составляющая. Уравнение (1.37) описывает процесс распространения плоской электромагнитной волны с затуханием, вызываемым диссипацией энергии вследствие проводимости. Формально (1.37) может быть сведено к (1.7), если ввести комплексный волновой вектор или (что согласно (1.15) эквивалентно) комплексный показатель преломления

 

`n = n – ig.                                                 (1.38)

 

Здесь п — действительная часть, равная введенному по (1.14) показателю преломления, а g – коэффициент экстинкции. Подставляя (1.38) в (1.15) и далее в формулу плоской волны (1.8), ограничиваясь при этом одномерным случаем (1.9), получаем

                        (1.39)

Это формула плоской волны с амплитудой, экспоненциально убывающей по мере проникновения излучения в поглощающую среду. Феноменологическое рассмотрение ослабления интенсивности света, распространяющегося в поглощающей среде, приводит к закону Бугера – Ламберта:

 

I(x) = I0exp(-c×x),                                                (1.40)

 

где c — экспериментально измеряемый линейный показатель поглощения. Учитывая квадратичную связь I0 с Е0 [см. формулу (1.13)], получаем

 

                                          (1-41)

 

Поскольку в эксперименте измеряется длина волны света в вакууме lв, а не в среде l, то обычно связь линейного показателя поглощения с коэффициентом экстинкции задается в виде

 

c = 4pg/lв.                                                (1.42)

 

Если комплексное значение показателя преломления (1.38) ввести в формулы, определяющие коэффициенты отражения и пропускания, то получим их обобщение для случая поглощающей среды. В частности, для нормального падения  луча  из  вакуума  (n1 = 1)  на поверхность поглощающей среды  (п*2 = п – ig)  имеем

 

                         (1.43)

 

При g®0 (1.43) переходит в (1.32), а при g®¥ R^®1, т. е. сильно поглощающее вещество ведет себя как металлическое зеркало. Закон сохранения энергии [третье уравнение в (1.30)] в случае поглощающей среды принимает вид:

R + T + A = 1,                                           (1.44)

или в дифференциальной форме

 

r + t + a = 1,                                            (1.44а)

 

где A(a) и T(t)—доли энергии волны, поглощенной в слое вещества и прошедшей через этот слой.

Проанализируем роль еще одного отличия реальных потоков излучения от идеализации § 1.1 — немонохроматичность световых волн. Для этого необходимо учитывать дисперсию, т. е. зависимость фазовой скорости волны от частоты (или частотную зависимость показателя преломления). Согласно классической теории замедление и поглощение световой волны в веществе обусловлено ее взаимодействием с элементарными атомными осцилляторами этого вещества. В простейшем приближении, когда все осцилляторы одинаковы, не взаимодействуют друг с другом и имеют собственные частоты колебаний w0, решение уравнения вынужденных колебаний, возбуждаемых внешней силой, изменяющейся с частотой w, дает

 

                             (1.45,

                                    

 

где N — концентрация осцилляторов, mе и q – масса и заряд электрона, f – константа, определяемая природой осциллятора.

Из формул (1.45) видно, что и п, и g должны менять ход своих частотных зависимостей вблизи резонансной частоты w = w0, что, как правило, и наблюдается экспериментально (рис. 1.7). Вдали от резонанса (w < w0 или w > w0) наблюдается нормальная дисперсия, для которой характерен рост п при увеличении w, около w = w0 – аномальная дисперсия. Для этой же области характерен и максимум поглощения. Обычно даваемые в справочниках значения п соответствуют w®0. Количественной мерой дисперсии служит величина DN/Dl или в пределе dn/dl, иногда ее и называют дисперсией D. Если распространяющаяся волна включает в себя группу монохроматических волн, занимающих полосу Dl, то согласно (1.16) и с учетом (1.15) ее групповая скорость

vг = vф(1-lD/n) = vфnг/n,                                   (1.46)

где vф = с/n – фазовая скорость, соответствующая частотному «центру» группы волн, а nг = п – lD — групповой показатель преломления.

Важнейшее практическое следствие дисперсии состоит в том, что по мере распространения в среде оптический сигнал «расплывается», т. е. происходит то же самое, что и с электрическим сигналом, распространяющимся по цепям, содержащим реактивности: искажение фронта и среза и увеличение общей длительности импульса. Оценки показывают, что уширение оптического импульса оказывается пропорциональным l1/2, где l — расстояние, пройденное им в диспергирующей среде.

Понятие дисперсии в более общем смысле как эффекта зависимости фазовой скорости волны от волнового вектора уже встречалось при анализе модового состава излучения, распространяющегося в волноводах [см. формулу (1.25)]; отличие состоит в том, что там дисперсия обусловливалась геометрическими факторами, а не тем, что D = Dn/Dl ¹ 0, поэтому она имеет место и для вакуума (n = 1). Эта модовая дисперсия важна, в частности, в системах волоконно-оптической связи.

В заключение отметим, что имеются и другие формы неидеальности оптической среды (шероховатость границ раздела, мутность, наличие статистически распределенных неоднородностей и т. п.), но их анализ (математически более сложный) основывается, как правило, на материале, рассмотренном в данном параграфе.