Olufsen M.S., Peskin C.S., Kim W.Y., Pedersen E.M., Nadim A., and Larsen J.: Numerical Simulatoin and Experimental Validation of Blood Flow in Arteries with Structured Tree Outflow Conditions
Исходный URL:http://www4.ncsu.edu/~msolufse/ABE01281.pdf

Числовая модель кровотока в артериях с древовидной структурой течения и экспериментальная её проверка

Резюме - Кровоток в больших системных артериях моделируется, используя одномерные уравнения, полученные из осесимметричных уравнений Навье-Стокса для потока в гибком и заостряющемся сосуде. Артериальное дерево сокращено после первых немногих генераций больших артерий с остающимися небольшими артериями и артериолами, обеспечивающими граничные условия оттока для больших артерий. Моделируя небольшие артерии и артериолы как структурированное дерево,полуаналитический подход, основанный на линеаризовавшей версии управляющих уравнений может использоваться, чтобы получить экспрессию для корневого сопративление структурированного дерева в частотной области. В области времени, это обеспечивает присущее граничное условие оттока. Структурированное дерево - бинарное асимметричное дерево, в котором радиусы дочернего сосуда измерены линейно с радиусом родительского сосуда. Кровоток и давление в большом сосуде вычислены как функции времени и осевого расстояния в пределах каждой из артерий. Сравнение между моделями и измерениями магнитного резонанса в восходящей аорте и девяти периферических местоположениях в одном человеке показывает превосходное соглашение между двумя.

Ключевые слова - Артериальный кровоток, Артериальное моделирование, моделирование Кровотока, Артериальные условия оттока, Биогидродинамика, Математическое моделирование.

ВВЕДЕНИЕ

Цель этой работы состоит в том, чтобы разработать и использовать одномерную жидко-динамическую модель, предсказывая кровоток и давление в системных артериях в любой точке сосуда. Такая модель может использоваться, чтобы изучить профиль потока и прижимных волн, поскольку они расходятся по артериям. Форма волн изменяется из-за артерий, изменяющих геометрию и структуру.

Системные артерии - гибкий сосуд, который заостряется по их длине и становится более жестким с меньшими радиусами. Они организованы в раздваивающемся дереве, в котором площадь поперечного сечения сосуда расширяется приблизительно от 5 см² в аортальном корне приблизительно к 400 см² в артериолах. Расширение встречается, потому что в каждом раздвоении объединенная площадь поперечного сечения дочернего сосуда является большей чем родительского сосуда, даже при том, что площадь поперечного сечения каждого сосуда дочери является меньшей чем область родительского сосуда. Кроме того, в дистальном конце артериального дерева, на артериолярном уровне, есть высокое сопротивление к потоку. В результате поток и прижимные волны отражены, и отраженные волны размножаются назад через артериальное дерево. Например, отраженная волна уменьшена у некоторых людей, страдающих от диабета, или также сосудистые болезни, типа атеросклероза, замечено, что люди с более жесткими артериями имеют менее явную отраженную волну, но увеличенные диастолические и систолические давления. Профили потока и прижимных волн изменяются значительно даже среди здоровых людей Следовательно, будучи в состоянии строить модель, основанную на взвешенной геометрии, и единственное атравматичное измерение потока в восходящей аорте позволит нам изучить формы волны для любого данного субъекта. Вычисленное давление и профили потока могли использоваться как часть диагностического метода. Например, для данного субъекта, взвешенные патологические профили потока могли быть по сравнению с вычисленными здоровыми профилями потока. Исследования того, как параметры модели должны измениться, чтобы моделировать взвешенные патологические профили потока, могли бы привести к лучшему пониманию патологического состояния. Кроме того, вычисление потоков и прижимных профилей могло использоваться в связи с имитаторами, например, в хирургическом или имитаторами анастезии.

В этой статье мы используем одномерную модель гидроаэродинамики, разработанную ранее для моделируемого потока сравнения социологического исследования и прижимных волн с потоками, полученными, используя методы магнитного резонанса. Геометрия (длины, вход и радиусы выхода) сосуда получена, используя измеренные данные от одного субъекта, и другие свойства сосуда (главным образом эластичность стен и периферических сопротивлений) основаны на предыдущей модели, но с параметрами, приспособленными, чтобы сравниться со взвешенными данными. Кроме того, уравнение, определяющее, как изменение давлений от родительского сосуда в его дочерей было изменено. Наконец, в нашей предыдущей работе, жидкая динамическая модель была заявлена, но не получена; таким образом мы обеспечиваем полное дифференцирование уравнений и заявляем, что алгоритмы имели обыкновение решать их. Модель состоит из двух частей: большие артерии, в которых кровоток и давление предсказаны в любой точке по сосуду, и небольшим артериям, в отношение которых между потоком и оказывают давление на граничные условия оттока выработок для больших артерий (см. рис. 1). Кровоток и давление в системных артериях (большой и небольшой сосуд) определены, используя несжимаемые осесимметричные уравнения Навье-Стокса для Ньютоновой жидкости. Одномерная модель получена, интегрируя эти уравнения по площади поперечного сечения сосуда. Дерево, представляющее большие артерии исходит от сердца и включает одну или две генерации от аорты, подвздошных, и бедренных артерий. Геометрия большого сосуда (длины и диаметры) подражает фактической геометрии артерий. Эти данные получены методами магнитного резонанса. Так как мы интересуемся предсказанием потока и оказываем давление на волны для данного субъекта, длины и диаметры для всего сосуда должны быть преданными человеческому артериальному дереву. Однако, чтобы ограничивать

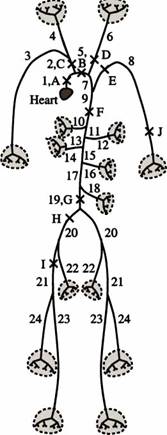
РИСУНОК 1. Системное артериальное дерево. Большие артерии смоделированы как двоичное дерево, где геометрия сосуда определена от измерений магнитного резонанса. Небольшие артерии смоделированы как структурированные деревья, присоединенные в терминалах большого сосуда. Геометрия структурированных деревьев не подражает фактической геометрии сосуда, но основана на общих статистических отношениях, которые оценены от литературных данных. Количество сосудов относящихся к различным сегментам больших артерий, и измерения этих сегментов даются в Таблице 1. Символы показывают десять местоположений, где потоки были измерены. Данные для них также определены в Таблице 1. Чтобы избегать слишком многих экспонатов из-за потока области входа, где только возможно, потоки измерены 2 см вне раздвоений.

модель мы сделали следующие исключения: Эти две коронарных артерии, межреберные артерии, артерии, выполняющие переход от брюшнополостной оси, и различных ветвей от подключичного, плечевого, и каротидного сосуда не учтены. Настоящее артерий с обеих сторон тела смоделировано тождественно. Они включают почечное, каротидный, подключичный, плечевой, подвздошный, и бедренные артерии. Коронарные артерии не включены, потому что приток в аорту от аортальной лампы измерен в восходящей аорте мимо коронарного раздвоения. Однако, коронарные артерии берут приблизительно 4 %-5 % функционального состояния сердца, и следовательно они должны быть включены, если приток в аорту измерен сразу после аортальной лампы.

Модель Кровотока и Проверка правильности в Больших Артериях

Межреберные артерии берут меньше чем 1 % функционального состояния сердца и, следовательно, их пренебрежение не изменяет вычисленные потоки значительно. Остающиеся артерии, не включенные в модель - вне начального разветвления от аорты, например, ветви от брюшнополостной оси. У нас нет никаких измерений в этих артериях, и включая их увеличивли бы значительно вычислительное время . Наконец, левые и правые артерии смоделированы как идентичные, так как мы только измерили геометрию в одной стороне.

Небольшие артерии смоделированы как бинарные асимметричные структурированные деревья, присоединенные в терминалах больших артерий (см. рис. 2). Каждый сосуд в пределах структурированных деревьев смоделирован как прямой сегмент послушного сосуда. В отличие от больших артерий, структурированные деревья не подражают фактической геометрии сосуда, но основаны на общих статистических отношениях, которые оценены из литературных данных.

БОЛЬШИЕ АРТЕРИИ

Предсказание кровотока и давления в послушном сосуде требует трех уравнений. Два уравнения гарантируют сохранение объема и импульса, и уравнение состояния связывает жидкое влияние на стену сосуда к ее послушным свойствам.

Типичный сосуд смоделирован как осесимметричный послушный цилиндр. Скорость жидкости, замкнутой в пределах цилиндра обозначена u = [ wr (r, x, f), wx (r, x, f)], где r - радиальная координата, x - позиция по сосуду, t - время, u_r – радиальная скорость, и u_x - осевая скорость. Стенка кровеносного сосуда, как предполагают, является непроницаемой. Следовательно, нескользящее условие удовлетворено, равняется ли скорость жидкости в стене скорости стены. Плотность p и вязкость взята}, чтобы быть постоянной. Допустим p (x, t) представляют давление жидкости и допускаем p0 (который является постоянным), представляют диастолическое давление. Мы предполагаем, что давление не изменяется очень по площади поперечного сечения сосуда, то есть, p приблизительно независим от r. Допустим R(x, t) радиус сосуда и допустим A( x, t) = πR² ( x,t) быть соответствующей площадью поперечного сечения. Сосуд, как предполагают, заостряется по экспоненте, то есть., равновесный радиус - r₀ (x) = r_texp ( log ( r_b /r_t) x / L ) когда p (x, t) = p₀ . Здесь, реальный масштаб времени r_t и r_b обозначают вход (вершина) и выход (основание) радиусы сосуда, и L >обозначает длину сосуда. Наконец, предполагается, что стена сосуда переносит радиальные движения только, то есть, что стена сосуда продольно привязана.

Уравнения динамики жидкости для Больших Артерий

Уравнение неразрывности. Для осесимметричного потока, уравнение неразрывности требует, чтобы дивергенция скоростной области обратилась в нуль, уступаясь

Кроме того, начиная с площади поперечного сечения Ur

Давайте определим

Так как сосуд продольно привязан (то есть, переносит радиальное движение только), и жидкость придерживается стены сосуда (из-за нескользящего условия)

как поток (объем/время) через сосуд. Тогда, одномерное уравнение неразрывности может быть получено нас-

мг (3) - (5) в (2):

Уравнение Импульса. Для осесимметричного потока без водоворота читает уравнение x-импульса

Первые три условия представляют осевую акселерацию жидкости, и остающиеся условия представляют сумму всех сил, действующих на жидкость. В этой модели силы состоят из прижимных и вязких вкладов ( v - кинематическая вязкость). Вообще, предыдущее уравнение содержит дополнительный вязкий элемент, действующий в продольном направлении ( νδ ² u_x /δx²) . В этом дифференцировании мы пренебрегли продольным вязким элементом, так как это является небольшим по сравнению с радиальным элементом

[правая сторона (7)]. Продольный вязкий элемент является небольшим, потому что кровеносные сосуды очень длинны по сравнению с их радиусами.

Как в случае уравнения неразрывности одномерная модель получена, интегрируя по площади поперечного сечения, имея в виду, что p принят как постоянная по той области

Здесь u_x ( x, t) - осевая скорость вне пограничного слоя. Согласно Lighthill толщина пограничного слоя S (для больших артерий) может быть оценена от ( ν/ω)^1/2 = ( νT / (2π R )) ≈0.1 см, где кинематическая вязкость ν=0.046 см²/ с , ω - угловая частота, и период кардиального цикла T = 1.1 с. Интегралы в (9) могут быть выражены как степенной ряд в δ:

Используя уравнения (3) и (5) первый элемент в (8) может быть написан как

Через интегрирование по частям, уравнение непрерывности (1) и отношения в (3) может использоваться, чтобы упростить второй элемент (8):

Объединение этих двух условий, дает

Вязкая тормозная, сила может быть оценена, используя скоростной профиль в (10):

Объединение более ранних условий с остающимися условиями в (8) дает

Пока мы не сделали никаких предположений о форме скоростного профиля. Для пульсирующего ламинарного потока в немного заостренном сосуде, скоростной профиль является довольно плоским за исключением тонкого пограничного слоя ширины S <R, в котором переходит в нулевую скорость в стене сделано (нескользящее условие) .Основаясь на этих соображениях, мы предлагаем следующую модель для скоростного профиля

Соблюдение ведущих условий в каждом компоненте и вставке их в (9) выработки одномерное уравнение

Young и Tsai среди других определили вязкое напряжение как комбинация двух элементов одно составление части в фазе со средней скоростью и вторым элементом, который является членом пропорции к производной времени скорости. Их дифференцирование основано на колебательном потоке в твердом сосуде, где неустойчивый элемент включен. В твердом сосуде ux может быть найден в терминах Бесселевых функций с комплексными аргументами в зависимости от частоты колебательного потока. Результат может быть расширен в пределе или небольших или больших частот. В низком частотном предельном Пуазейлевском течении восстановлен, и в высоких частотах получен эквивалент (11). Решение Young и Tsai эквивалентно тому, что мы получили для небольших артерий, где вязкие эффекты более значительны (см. секцию на Небольших Артериях). Для больших артерий вязкие эффекты являются небольшими, и следовательно, мы не включили неустойчивый элемент в более раннее уравнение. Однако, такой элемент может легко быть включен, изменяя коэффициент dq / dt в уравнении импульса (12).

Непрерывность (6) и импульс (12) уравнения не могут быть решены аналитически, таким образом к числовому методу призывают. В этой работе, уравнения решены, используя двухступенчатый Lax -Wendroff метод, который требует, чтобы уравнения были написаны в форме сохранения. Форма сохранения может быть получена, представляя количество B определенный ниже. Отметьте, что площадь поперечного сечения A расценена как функция давления

отношения получены из линейной теории эластичности. Используя исключительно упругую модель обоснованно, потому что вязкоупругие эффекты являются небольшими в пределах физиологических диапазонов давления , Предполагают, что сосуд - проспект, что стены являются тонкими (час/запрос < час , являющийся стенной толщиной), что нагружение и деформация осесимметричны, и что сосуд привязан в продольном направлении. Следовательно, внешние силы могут быть уменьшены до усилий, действующих в круговом направлении и от того, что известно как закон Лапласа, которым круговое растяжимое напряжение может быть найдено в форме

где ( r - ro )/ro - соответствующее круговое напряжение, E - модуль Юнга в круговом направлении, ao=ax = O.5 - отношения Пуассона в круговых и продольных направлениях. Решая для p (x, t) -p0 дают

Последний элемент может быть оценен явно и может, поэтому, быть добавлен к обеим сторонам уравнения импульса (12). В результате форма сохранения получена

Уравнения (6) и (13) составляют нашу элементарную одномерную модель для распространения кровотока и давления. Однако, есть два уравнения для трех зависимых переменных, p, q, и A. Поэтому, третьи отношения (статическое уравнение) необходимы