ВВЕДЕНИЕ

В последние годы одним из направлений развития компьютерных технологий является обработка цифровых изображений: улучшение качества изображения, восстановление поврежденных изображений, распознавание отдельных элементов и всего изображения в целом. Особое место в науке занимает задача распознавания изображения.

В настоящее время в медицинских учреждениях Украины нашли широкое применение компьютеризированные диагностические системы, использующие для выявления патологий различные изображения, в том числе и ультразвуковые снимки. Однако в большинстве этих систем недостаточно используются возможности современных ЭВМ для вынесения предварительного диагноза.

Целью данной работы является создание автоматизированной системы распознавания текстур изображений на основании методов, инвариантных к изменений угла поворота и масштаба. Данная система может быть адаптирована для использования ее в различных областях, например, в медицине – для автоматизированной обработки изображений УЗИ. Также подобная система может быть полезной в металлургии для анализа качества поверхности металла, для определения его зернистости, а также в пищевой промышленности, например для определения качества мяса (его пригодности).

Наиболее важными подсистемами в разрабатываемой системе являются:

1. Подсистема обработки изображения (текстурный анализ).
2. Подсистема поддержки принятия решения.

Особое значение имеет разработка математического обеспечения первой выделенной подсистемы. Текстурный анализ – это анализ, который осуществляется по признакам, рассчитанным по самому изображению. Существуют различные методы его реализации.

1. АКТУАЛЬНОСТЬ ПОСТАВЛЕННОЙ ЗАДАЧИ

В связи с актуальностью проблемы распознавания изображений, в последние годы текстурный анализ получил активное развитие. Имеет место как создание новых методов, так и модифицирование уже существующих, причем оба направления дают весомые результаты.

Исходя из цели данной работы необходимо выбрать такой метод текстурного анализа, на результаты классификации которого не влияло бы изменение масштаба и поворот изображения. Этот критерий существенно сужает диапазон существующих методов, но тем актуальнее становится поставленная задача. Например, при проведении ультразвукового обследования человека изображение одного и того же его органа не может на разных снимках представляться в абсолютно одинаковом положении. Один и тот же орган будет расположен под разными углами и с небольшой разницей в масштабе. Проблема состоит в том, что если не учитывать эти условия, то при анализе изображений одного и того же объекта, расположенного под разными углами и/или в разном масштабе, для одной и той же текстуры будут получены разные признаки, то есть она будет распознана по-разному, неверно. Таким образом, чтобы получить объективные результаты распознавания текстур, для текстурного анализа необходимо использовать метод, инвариантный к изменению угла поворота и масштабированию объекта на изображении.

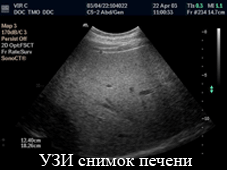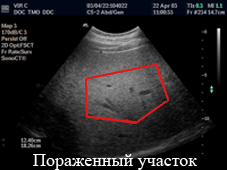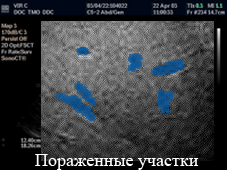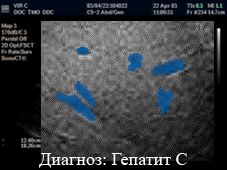
Рисунок 1.1 Вынесение диагноза на основании текстурного анализа УЗИ изображения печени человека (анимация, циклически повторяется 5 раз)

2. ОБЗОР СУЩЕСТВУЮЩИХ МЕТОДОВ

2.1. Метод, основанный на представлении спектральных сигнатур направления изображения текстуры

Мощным инструментом в инвариантном анализе текстуры является анализ Фурье. Рассматриваемый метод является достаточно простым в отношении вычислений, но в то же время эффективным для распознавания текстур, инвариантных к вращению. На основании представления вращения получают функцию распределения сигнатуры. Применяя расширение Фурье на этой функции, было достигнуто постоянство при вращении.

Проведением экспериментов по данному методу одними из последних проводили Дж.Жанг и Т.Тан [1]. Они исследовали полноценность предложенных сигнатур на базе данных из 1000 текстур с произвольными углами поворота. Обширное сравнительное исследование признаков Габора показало, что предложенный алгоритм очень эффективен в инвариантной классификации текстуры.

Ниже приведено описание математической основы данного метода.

Пусть f(x,y) – первоначальное изображение текстуры. Определим проекцию f(x,y) на линию l под углом к оси x:

где

(2.1)

Если =0, то получаем вертикальную проекцию на ось x:

(2.2)

Функция проекции может получить периодическую функцию текстур в разных направлениях.

Проекция функции f(x,y) на линию, расположенную под углом, может быть оценена с помощью ее Фурье-версии на линию под углом .

Пусть функция f_r(x_r,y_r) является повернутой версией функции f(x,y). Тогда взаимосвязь этих двух изображений формулируется следующим образом:

fr(xr,yr)=f(x,y);

(2.3)

Известно, что при повороте первоначальной текстуры на какой-то угол спектр частотной области также сдвигается на этот угол. Это свойство поворота преобразования Фурье. Связь между спектром первоначального и повернутого изображения описывается следующим образом:

(2.4)

где - преобразование Фурье первоначальной текстуры f(x,y),

- преобразование Фурье текстуры f_r(x_r,y_r),

- обратная транспонированная матрица матрицы R.

Одномерное преобразование Фурье для выражения (2.2):

(2.5)

Полученное выражение может быть записано в другой форме:

(2.6)

Пусть , – преобразование Фурье проекции f(x,y) на линию под углом ; – преобразование Фурье проекции f_r(x_r,y_r) на линию под углом . Их связь представляет собой:

=

(2.7)

Центральный момент выражения (2.7):

(2.8)

где - средние значения .

Вычислим спектр сигнатур с углом и (=+):

(2.9)

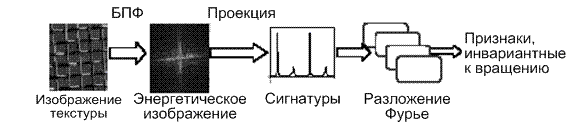
Таким образом получили спектральные сигнатуры направления T(). Очевидно, что текстурная сигнатура зависит от поворота и является функцией от с периодом 2.

T()=T(), если -=. Это подразумевает, что поворот входного изображения f(x,y) на угол эквивалентен сдвигу его спектральных сигнатур на такое же число вдоль оси направления.

Схематическая диаграмма получения признаков текстуры, инвариантных к вращению представлена на рис.2.1.

Рисунок 2.1 Схематическая диаграмма получения признаков текстуры, инвариантных к вращению

2.2. Метод, основанный на комплексном вейвлет-преобразовании «двойного дерева»

Работу по обобщению и оптимизации данного метода одними из последних проводили М.Пикеринг, М.Фратер и Дж.Арнольд [2].

Комплексное вейвлет-преобразование «двойного дерева» является формой дискретного вейвлет-преобразования, которое производит комплексные оценочные коэффициенты. Это осуществляется с помощью двойных деревьев фильтров, которые независимо производят реальные и мнимые ответы. Свойства КВП-ДД включают:

• приблизительную инвариантность к сдвигам;
• фильтры в двумерной выборке направленной избирательности;
• совершенная реконструкция сигнала по коэффициентам;
• ограниченная избыточность: 2:1 для одномерной и 4:1 для двумерной функции;
• эффективное вычисление O(n) для одномерной и O(n²) для двумерной функции.

Для двумерной функции фильтры подобны фильтрам Габора, поэтому КВП-ДД может быть эффективным способом произвести коэффициенты отклика подобные коэффициентам Габора. На каждом уровне производится 6 подполос, которые обнаруживают признаки, различающиеся на 30^o.

ДВП обеспечивает инструмент многомасштабного анализа для рассмотрения сигналов. Это преобразование может быть представлено как полосно-пропускающий фильтр, фильтры которого чувствительны к частотам по двухэлементным шкалам. На каждом уровне анализа, входной сигнал разложен на функции по базису вейвлет:

(2.10)

где Ф – материнская вейвлет-функция, S – целое число для обозначения масштаба, К – число, определяющее сдвиг. Функции базиса вейвлета для КВП-ДД определяются таким же образом, как и для ДВП.

Для анализа признаков, инвариантного к изменению масштаба, используются фильтры, равные по амплитуде на каждом уровне анализа, поэтому можно убрать множитель . Получается новое семейство функций базиса вейвлета:

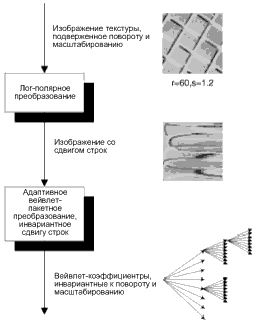
Нет необходимости изменять фильтры для КВП-ДД. Нужно только умножить выходные коэффициенты на . Обозначим КВП-ДД^# и ДВП^# как преобразования, использующие Ф^#_s,k(x) для своих базисных функций вейвлета.

2.3. Метод, основанный на использовании лог-полярных энергетических вейвлет-сигнатур

Этот метод предлагает эффективную схему классификации текстур, инвариантных к вращению и масштабированию, использующую лог-полярные вейвлет сигнатуры. Выделение признаков, инвариантных вращению и масштабированию, для данного изображения включает применение лог-полярного преобразования для устранения эффектов вращения и масштабирования; затем производится лог-полярное изображение со сдвигом рядов, которое потом передается к адаптивному вейвлет-преобразователю, инвариантному сдвигу рядов, для устранения эффекта сдвига рядов.

По алгоритму данного метода [3] происходит извлечение лог-полярных вейвлет сигнатур энергии, инвариантных к вращению и масштабированию, для данного изображения, которые могут быть получены с помощью лог-полярного преобразования на изображении, а затем с помощью адаптивного вейвлет-преобразования, инвариантного сдвигу рядов (как показано в рис.2.2).

Рисунок 2.2 Выделение вейвлет-коэффициентов, инвариантных к повороту и масштабированию, из изображения текстуры, подверженной повороту и масштабированию

Алгоритм лог-полярного преобразования разделён на 2 основных этапа. На первом этапе радиус наибольшего круга внутри данного изображения используется как сканирующая линия выборки (сэмплирования) S раз от 0^o до 360^o для получения эквивалентной Sx[N/2] полярной формы. Так, формально, полярная форма p(a,r) данного NxN изображения f(x,y) может быть вычислена как:

(2.12)

для а=0,…,S-1, и r=0,…,[N/2]-1.

На втором этапе логарифмическая функция применяется ко всем значениям радиуса в полярной форме, и их выходные величины квантуются на R состояний. Получаем SxR лог-полярное изображение для заданного NxN изображения

(2.13)

для i=0,…,S-1, и j=0,…,R-1.

3. ОБОБЩЕНИЕ РЕЗУЛЬТАТОВ НАУЧНОГО ПОИСКА И АНАЛИЗА

Проанализировав имеющиеся результаты работы рассмотренных методов: метода, основанного на представлении спектральных сигнатур направления изображения текстуры, метода, основанного на комплексном вейвлет-преобразовании «двойного дерева» и метода, основанного на использовании лог-полярных энергетических вейвлет-сигнатур; можно сделать следующие основные выводы:

• Метод, основанный на представлении спектральных сигнатур направления изображения текстуры, имеет достаточно высокую среднюю точность 98.90% классификации. Однако этот метод является инвариантным только к изменению угла поворота изображения. Инвариантности к масштабированию изображения он не обеспечивает, что является серьезным недостатком, и поэтому в представленном виде для данной исследовательской работы он не подходит. Однако в дальнейшем возможна доработка этого метода, например, можно сделать попытку до или после расчета признаков использовать одно из известных преобразований, дающих инвариантность к масштабу (преобразование Радона, лог-полярное преобразование).
• В методах текстурного анализа инвариантность к изменению угла поворота и масштаба обеспечивается одним из двух способов:
  1. С помощью преобразования изображения до или после расчета признаков этого изображения. Инвариантности распознавания текстур к изменению угла поворота и/или масштаба можно добиться, используя, например, преобразование Радона или лог-полярное преобразование;
  2. С помощью использования в расчетах признаков текстур, инвариантных к изменению угла поворота и/или масштаба.

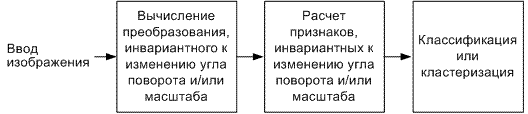
Таким образом, рассмотрев представленные методы текстурного анализа, инвариантные к изменению угла поворота и масштаба изображения, ознакомившись с их структурой, можно составить обобщенную структуру подсистемы обработки изображений, инвариантных к изменению угла поворота и масштаба. Данная структура представлена на рис.3.1.

Рисунок 3.1 Обобщенная структура подсистемы обработки изображений, инвариантных к изменению угла поворота и масштаба

Классификация – это процесс распределения по классам элементов изображения на конечное число классов на основе значений их атрибутов (признаков). Если элемент изображения удовлетворяет определенному условию классификации, то он относится к определенному классу, который соответствует этому условию.

Кластеризация – это процесс разделения изображения на классы (кластеры) на основе некоторой меры сходства элементов этого изображения.

4. ОСНОВНЫЕ ЗАДАЧИ ИССЛЕДОВАНИЯ

Вследствие обобщения результатов научного поиска и анализа приведенных выше методов текстурного анализа, а также на основании представленной структуры подсистемы обработки изображений, инвариантных к изменению угла поворота и масштаба, можно сформулировать постановку задачи для построения подсистемы обработки изображений, инвариантных к изменению угла поворота и масштаба:

1. Обоснование и выбор методов преобразования изображения, позволяющего получить инвариантность к изменению угла поворота и/или масштаба этого изображения;
2. Обоснование и выбор методов расчета признаков изображения, позволяющих получить инвариантность к изменению угла поворота и/или масштаба этого изображения;
3. Обоснование и выбор методов классификации изображения;
4. Математическое моделирование и программная реализация методов распознавания текстур, построенных на основании выбранных методов преобразования и расчета признаков с целью выбора метода, обеспечивающего наиболее высокую точность и наименьшую зависимость от масштаба и поворота;
5. Выбор значений параметров метода, обеспечивающего наиболее высокую точность классификации изображения;
6. Апробация метода на прикладных задачах (УЗИ, дефектоскопия).

ЗАКЛЮЧЕНИЕ

Анализ текстуры – фундаментальная проблема в обработке изображения, машинном представлении и их использовании, например, при объектном распознавании, дистанционном воздействии, восстановлении изображения на основе его содержимого и так далее. Эта тема активно исследуется в течение более трех десятилетий, но ощутимое развитие она приобретает только в последние годы.

Особенно актуальна эта проблема распознавания текстур для данной работы. На разных УЗИ снимках один и тот же орган одного человека не может быть представлен в том же самом положении. В связи с этим в данной работе рассматриваются методы текстурного анализа, инвариантного к изменению угла поворота и масштабирования изображений.

СПИСОК ИСТОЧНИКОВ

[1] «Новые текстурные характеристики и их использование в классификации текстур, инвариантных к изменению угла поворота», Джианго Жанг, Тиену Тан, 2001.

[2] «Метод распознавания текстур, инвариантный к изменению угла поворота и масштаба, основанный на комплексном вейвлет-преобразовании «двойного дерева», Эдвард Х. С. Ло, Марк Пикеринг, Майкл Фратер, Джон Арнолд, 2004 IEEE.

[3] «Логарифмически-полярные вейвлет-сигнатуры для классификации текстур, инвариантных к вращению и масштабу», Чи-Мэн Пан, Мун-Чуен Ли, 2003 IEEE.

[4] http://gis-lab.info/qa/genclass-erdas.html – информация о классификации изображений.

Примечание:

Данный автореферат на является окончательной версией автореферата магистерской работы. Готовность магистерской работы планируется на декабрь 2006 г. За окончательной версией обращаться к автору.