ФЛИКЕР-МОДЕЛЬ С РАСШИРЕННЫМ ЧАСТОТНЫМ ДИАПАЗОНОМ КОЛЕБАНИЙ НАПРЯЖЕНИЯ

Э.Г. Куренный, Е.Н. Дмитриева, В.А. Петросов, К.В. Цыганкова

Донецкий национальный технический университет

Annotation – The groundlessness of the norms of the voltage fluctuation in the field of less then 1 Hz frequencies. It is offered to lift limits of minimum frequency by the way of taking into account the phenomenon of the slow adaptation.

Key words – EMC, dose of flicker, weighting filter, reduction of norms, slow adaptation of vision.

Под колебаниями напряжения понимают быструю составляющую процесса U(t) изменения действующих значений напряжения: разность U(t) между U(t) и его одноминутным трендом [1,2]. Колебания напряжения создают колебания светового потока ламп, которые вызывают фликер-эффект у людей, работающих при искусственном освещении. В общем случае допустимость колебаний оценивается лозой фликера напряжения. Периодические колебания напряжения простой формы можно оценивать по зависимостям размахов колебаний от их частоты (кривым размахов) при условии, что любая их точка дает допустимую дозу фликера.

В стандарте [1] указываются разные частотные диапазоны колебаний: взвешивающий фильтр (ВФ) фликерметра имеет частоту пропускания от 0,05 до 35 Гц, а нормы на размахи периодических колебаний установлены для частот всего от 0,5 до 24 Гц. В стандарте же [2] рис. 1 для колебаний в форме меандра приведен для частот F от 0,1 до 1620 мин^-1, т.е. для частот от 8,33·10^-4 до 13,5 Гц. Это объясняется тем. что при частотах менее 0,05 Гц требования к размахам колебаний устанавливались не с целью ограничения фликер-эффекта, а из условий обеспечения запуска электродвигателей [З]. Смешивать разные по смыслу оценки электромагнитной совместимости (ЭМС) не допустимо. Далее будем исходить из фликер-модели с минимальной частотой 0,05 Гц.

Однако в литературе по биомедицине (например, нет ограничений по частотному диапазону, поэтому нет оснований считать, что при частотах менее 0,05 Гц фликер-эффект отсутствует. Это подтверждается и инженерной практикой: так, в [5] нижний предел частот колебаний принят равным один раз в час, т.е. всего 1,4·10^-4 Гц. Устранение этого явного несоответствия является целью статьи.

СУЩЕСТВУЮЩИЙ ВЗВЕШИВАЮЩИЙ ФИЛЬТР

Не останавливаясь на проблеме учета утомления человека, отметим, что основу фликер-модели составляет линейный ВФ, который моделирует источник света, 1 реакцию (1) человека на колебания напряжения. ВФ описывается линейным дифференциальным уравнением II порядка с постоянными коэффициентами и состоит из трет последовательно соединенных фильтров: ВЧ - высотах частот, ВК - восприятия колебаний (термин наш), НЧ - нижних частот.

Фильтр ВЧ имеет пороговую частоту 0,05 Гц и представляет собой реальное дифференцирующее звено 1 с постоянной времени Т_k =3,1831 с и амплитудно-частотной функцией(AЧФ)

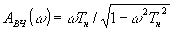     (1)

где w = 2p l - угловая частота

В фильтр ВК входят поел обязательно соединенные звенья: 2 - колебательное с коэффициентом передачи k = 1.74802 и постоянными времени Т_к1 = 0,015418 с, Т_к2 = 0,017385 с; 3 - форсирующее с Tф = 0,069811 с; 4 и 5 - апериодические (инерционные) первого порядка с Т_н1 = 0,12989 с и Т_н2 = 0,007267 с; 6 - дифференцирующее с постоянной времениТ_к2. Эти звенья имеют следующие АЧФ:

     (2)

.

,

     (3)

АЧФ фильтра ВК

     (4)

Фильтр НЧ 7 с пороговой частотой 35 Гц представляет собой фильтр Батерворта из трех колебательных звеньев с постоянными времени Т_Б1 = 0,0023537 с, Т_Б2= 0,004573 с, Т_Б3= 0,0064308 с., Т_Б4=-0,0087849 с. АЧФ фильтра

A_НЧ={ [ (1-w ²T_Б2²)²+w ²T_Б1² ] [ (1-w ²T _Б2²)²+w ²T_3>Б3^2] [ (1-w ²T_Б2²)²+w ²T_Б4²] }^-1/2.     (5)

Для того, чтобы выразить реакцию фильтра в относительных единицах (о.е.), вводится коэффициент kg =16 (о.е.)/(%). Этот коэффициент учитывается пропорциональным звеном 8.

Все фильтры и звенья соединены последовательно, поэтому АЧФ взвешивающего фильтра

А_ВФ(w )=kg A_<ВЧ(w )А_ВК(w )А_НЧ(w )     (6)

Рисунок 1 - Частотные характеристики ВФ

Рассчитанная по формулам (1) - (6) АЧФ представлена кривой 1 на рис. 1. Пороговой частоте 0,05 Гц отвечает значение 0,0067, которое можно считать границей практического затухания АЧФ. Кривая имеет максимум при частоте 8,85 Гц (в табл.В.1 из [2] - 0,146 мин^-1 (или 8,77 Гц), которая совпадает с резонансной частотой нервных клеток при восприятии электрических сигналов. В этой зоне даже очень малые размахи колебаний вызывают сильное воздействие на человека.

Переходная функция h(t) ВФ (кривая 1, рис.2) была найдена Л.В. Черниковой с использованием метода-парциальных реакций [5], согласно которому ВФ заменяется эквивалентной моделью из 11 параллельно включенных инерционных звеньев. Сумма переходных функций всех звеньев дает искомую функцию. Кривая 1 уменьшается за 0,27 с до значения 0,18%, которое составляет 0,02 от ее наибольшей ординаты.

ПРЕДЛАГАЕМОЕ РЕШЕНИЕ

Ограничение частотного диапазона значением 0.05 Гц представляется некорректным. Для объяснения причины этого принципиального недостатка существующей фликер-модели рассмотрим адаптацию зрения к изменению освещенности. Есть два вида адаптации: быстрая обусловлена электрическими процессами, а медленная - фотохимическими процессами в мозгу. Первая имеет постоянную времени порядка десятков мс и вызывает заметные субъективные ощущения у человека, особенно в зоне резонансной-частоты нервных клеток. Поэтому ее можно надежно оценить именно в области достаточно высоких частот. Медленная же адаптация имеет постоянную времени на три порядка большую, а ее действие примерно в 10 раз слабее. Это обстоятельство и объясняет, почему выполненные эксперименты не дали достоверных результатов в области низких частот.

Отсюда следует, что для распространения концепции фликер-модели на частоты менее 0,05 Гц необходимо учесть явление медленной адаптации. Для этого в существующем ВФ выделим звено быстрой адаптации и параллельно ему добавим звено медленной адаптации. Фильтр ВЧ при этом становится излишним.

В [6] указано значение 0,016 с постоянной быстрой адаптации. Близкой к ней является величина Т_к2 которую и примем для характеристики быстрой адаптации. Это явление моделируется реальным дифференцирующим звеном с передаточной функцией

W(s)=T_k2s/( T_k2s+1),     (7)

В существующем ВФ звено 6 дает только числитель передаточной функции (7). Для получения знаменателя к этому звену добавим инерционное звено 8 с постоянной времени Т_к2, но для сохранения АЧФ в области высоких частот в ВФ введем форсирующая звено 10 с той же -постоянной времени (рис.3). Прок - ведение передаточных функций звеньев 8 и 10 равно единице.

Медленная 2-аптация моделируется реальный дифференцирующим звеном 11 с коэффициентом передачи к_а2= 0,09 и постоянной времени Т_а2 = 70. Передаточная функция звена даются выражением

W_a2(s)=k_a2T_k2s/( T_k2s+1),     (8)

Коэффициент передачи k в формуле (4) обеспечивает равенстве единице ординаты АЧФ при резонансной частоте. Преобразование структуры ВФ нарушает это условие. Поэтому необходимо ввести нормировочный множитель 1/A_m, который можно учесть в любом из последовательно включенных звеньев. В результате передаточная функция предлагаемого ВФ (индекс “К”)имеет вид

W_k(s)=(T_k2+1)W_n(s)[ W_a1(s)+W_a2(s)] ,     (9)

где через

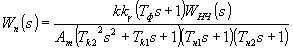     (10)

обозначена передаточная функция последовательно соединенных звеньев 2-5, 7 и 8.

ЧАСТОТНЫЕ ФУНКЦИИ

Звенья 11 и 12 имеют следующие АЧФ:

     (11)

     (12)

Заменив в (9) s на jw , где j=Ö -1, найдем АЧФ предлагаемого ВФ.

Рисунок 2 - Переходные функции ВФ

     (13)

Для определения нормировочного множителя необходимо вначале положить A_m = 1 и по формуле (13) рассчитать АЧФ, максимальная ордината которой дает фактическое значение A_m. Полученная с учетом этого значения АЧФ имеет единичную ординату при резонансной частоте (рис.1, кривая 2).

В области больших частот кривые 1 и 2 практически совпадают, а при малых частотах кривая 2 проходит намного выше. Пороговая частота для предлагаемого ВФ равна 10^-4 Гц, а не 0,05 Гц. Это означает, что учет медленной адаптации уменьшает нижний предел частот в 0,05/10^-4 = 500 раз.

Чем больше ордината АЧФ, тем жестче требования к ЭМС. Отношение ординат кривой 2 и 1 дает ориентировочную оценку степени занижения требований при использовании существующей фликер-модели. Например, при пороговой частоте 0,05 Гц фликерметра отношение ординат равно 21,4, а при пороговой частоте 0,5 Гц кривых размахов в [2] -1,82. Столь существенное занижение требований должно быть исключено.

Существующие нормы относятся к стандартной лампе накаливания 60 Вт, 230 В. Для учета фактического источника света теоретически необходимо разделить (6) или (13) на АЧФ стандартной лампы и умножить на АЧФ рассматриваемой лампы. Для практических целей целесообразно установить коэффициент пересчета для каждого вида ламп: как для АЧФ, так и доз фликера напряжения. Например, для люминесцентных ламп этот коэффициент равен 0,417.

Соответствующая АЧФ представлена на рис.1 кривой 3, которая проходит намного ниже кривой 2. Это объясняется тем, что при одних и тех же колебаниях напряжения колебания светового потока у люминесцентных ламп в 2,4 раза меньше, а потому человек утомляется меньше.

ПЕРЕХОДНЫЕ ФУНКЦИИ

Из-за сложности формулы (9) переходную функцию h_k(t) ВФ определить как обратное преобразование Лапласа от W_k(s)/s не представляется возможным. Для этой цели воспользуемся методом парциальных реакций. В отличие от существующего ВФ, в котором все звенья и фильтры соединены последовательно, предлагаемый ВФ имеет параллельно включенные звенья.

Поскольку метод парциальных реакций относится только к последовательному соединению, необходимо свести задачу к рассмотрению именно таких соединений. В соответствии со структурой формулы (9) для этого достаточно представить искомую переходную функцию в виде суммы

h_k(t)=h_n1(t)-h_n2(t),     (14)

двух составляющих, определяемым по передаточным функциям

W_n1,2(s)=(T_k2-1)W_n(s)W_a1,2(s),      (15)

каждая из которых относится к линейным системам с последовательными соединениями звеньев.

Эти системы не аналогичны, так как при умножении переходной функции звена 10 на W_a1(s) она

сокращается, а при умножении на W_a2(s) - нет. В результате первая система описывается дифференциальным уравнением 10 порядка, а вторая -11. Именно поэтому передаточная функция звена 10 не входит в формулу (10).

Если передаточная функция системы из последовательных звеньев имеет числитель P(s) и знаменатель в виде многочлена n-й степени, то постоянная времени и коэффициент передачи i-го парциального инерционного звена определяется по формулам [5]:

J₁=-1/s₁, a₁=,     (16)

где s_r - корни знаменателя, Т_nⁿ - общий множитель разложения знаменателя на множители s-s_r при r= 1,2,....n.

Знаменатели двух систем в (15) представляют собой комбинацию инерционных и колебательных звеньев. Инерционное звено с постоянной времени T_н имеет корень

-1/Т_н, а потому постоянная времени (но не коэффициент передачи!) совпадает с Т_н. Каждому колебательному звену отвечают два комплексных корня. Например, для звена 2

s_21,22=-a _2± jb ₂=25,049± j51,78 c^-1,     (17)

где

a ₂=T_k1/2T_k2²,

     (18)

В этом случае имеем два парциальных звена с постоянными времени (нумерация парциальных звеньев не совпадает с нумерацией исходных звеньев):

J_1,2=-1/s_21,22== 7,5709× 10^-3± j0,01558 c^-1.     (19)

Аналогично вычисляются остальные корни. В этом случае постоянные времени парциальных звеньев, помимо (19), составят:

J_3,4=T_{и 3,4}, J_5,6=(-1,1769± j4,4119)10^-3 c^-1,

J_7,8=(3,2154± j3,2517)10^-3 c^-1,     (20)

J_9,10=(-4,3925± j1,2723)10^-3 c^-1.

Коэффициент передачи i-го парциального звена

     (21)

при s=s_i

Для второй системы к постоянным времени (20) добавляется постоянная J₁₁ ⁼ Т_а2 11 парциального звена, а вместо (21) будут другие коэффициенты передачи при s =s_i:

     (22)

С учетом известной формулы для перехода функции инерционного звена получим составляющие переходной функции в виде суммы парциальных реакций:

,

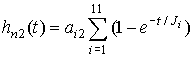     (23)

Несмотря на то, что выражения (16)-(22) содержат; мнимые величины, при суммировании согласно (23) и (14) остаются лишь вещественные величины.

Медленная адаптация значительно задерживает затухание переходной функции. Это и приводит к большему утомлению человека.

ЗАКЛЮЧЕНИЕ

Эмпирический подход к выбору АЧФ взвешивающего фильтра не позволяет учесть явление медленной адаптации. Поэтому существующие норм существенно занижают требования к колебаниям напряжения частотой 1 Гц и менее. Для устранения этого принципиального недостатка необходимо в существующий ВФ добавить блок медленной адаптации и исключить фильтр высоких частот, что позволит уменьшить нижнюю колебаний с 0,05 до 10^-4 Гц.

ЛИТЕРАТУРА

1. CEI/IEC 61000-4-15. Electromagnetic compatibility- Part 4, Section 15: "Flickermeter - Functional and design specification", 1997.

2. ГОСТ 13109-97. Межгосударственный стандарт Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения”. - Введ. в Украине с 01.01.2000.

3. C. Mirra, G. Sani. "Il fenomeno del flicker. Analiz delle sue caracteristiche. Techniche di misura e metodi del limitazione".- L'Elettrotecnica, 1987.

4. Ю.П. Шабанов-Кушнаренко, “Математическое моделирование некоторых функций человеческого зрения”. — В кн. Проблемы бионики. — М.: Наука, с. 39-45,1973.

5. E.G. Kourennyi, V.A. Petrosov, L.V. Chernikova. "Linear filtration on random processes in EMC models: the ''partial reaction" method". - Fifteenth International Wroclaw symposium and exhibition: Electromagnetic compatibility 2000. - Wroclaw: National Institute of Telecommunications, pp. 587-590, 2000, part II.