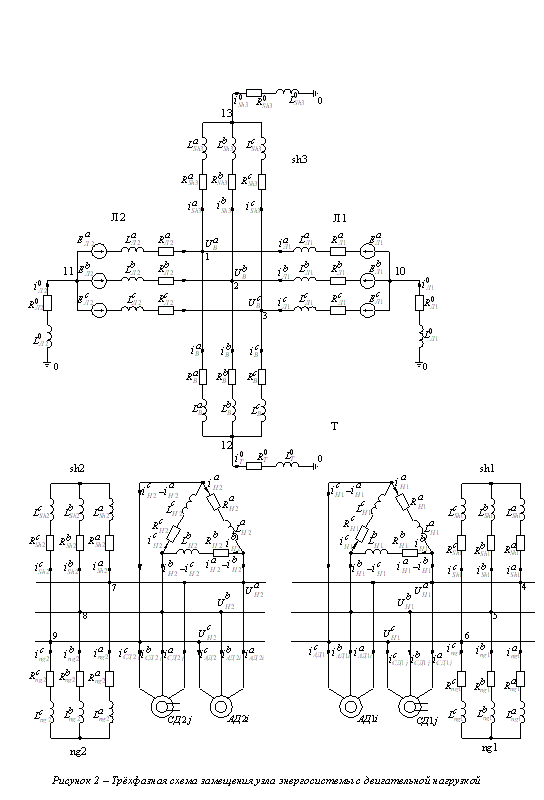ДонНТУ
>Портал магистров ДонНТУ
Биография| Библиотека|
Реферат| Ссылки |Отчёт о поиске|
Индивидуальное задание
Сивокобыленко В.Ф., Лебедев В.К., Кукуй К.А.
Донецкий
национальный технический университет
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ РЕЖИМОВ
ГРУППОВОГО ВЫБЕГА И САМОЗАПУСКА В СИСТЕМАХ ЭЛЕКТРОСНАБЖЕНИЯ С АСИНХРОННЫМИ И
СИНХРОННЫМИ ДВИГАТЕЛЯМИ
Рассмотрена математическая
модель узла двигательной нагрузки энергосистемы основанная на полных
дифференциальных уравнениях её элементов. Получены выражения для определения
напряжений в узлах расчетной схемы. Модель позволяет рассчитывать режимы
группового выбега, самозапуска при перерывах питания, вызванных симметричными и
несимметричными короткими замыканиями в схеме электроснабжения с асинхронными и
синхронными двигателями.
Системы
электроснабжения с асинхронными и синхронными двигателями получили широкое
распространение в различных отраслях промышленности: металлургических и
химических предприятиях, магистральных газо- и нефтепроводах, в системах
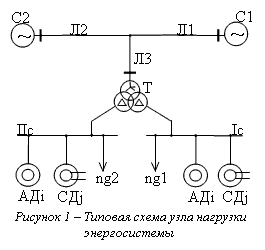
собственных нужд электростанции и др. Типовая схема таких систем
электроснабжения приведена на рис. 1. Для анализа их работы при кратковременных
нарушениях электроснабжения требуется учет токов подпитки места короткого
замыкания от двигательной нагрузки, определение частоты, фазы и уровня
напряжения на шинах питания двигателей, учет перетоков мощностей между
отдельными двигателями и узлами нагрузки при их групповом выбеге, выбор уставок
устройств релейной защиты и автоматики. При этом требуется определение
мгновенных значений параметров режимов (токов, напряжений, мощностей, моментов и
др.).
В работах, посвященных данной теме,
в основном рассматриваются узлы нагрузки, содержащие только асинхронные
двигатели [1 — 4], или только синхронные [5 — 8], и недостаточно освещен вопрос
анализа поведения комплексного узла нагрузки, состоящего из произвольного числа
асинхронных и синхронных двигателей, статической нагрузки. Кроме того, в
указанных работах и других [9 — 13] рассматриваются и анализируются в основном
перерывы питания, вызваны симметричными короткими замыканиями, тогда, как
известно, что в питающих сетях 110 — 330 кВ с глухим заземлением нейтрали
преобладающими являются однофазные короткие замыкания. Решение указанных
вопросов и явилось целью настоящей работы, в которой представлено математическое
описание коротких замыканий и режимов группового выбега и самозапуска
асинхронных и синхронных двигателей, реализованное в цифровой модели на ПЭВМ.
При разработке модели принимались общепринятые допущения для электрических машин
и трансформаторов (синусоидальность магнитного потока в зазоре, неучёт насыщения
магнитных потоков, симметрия фазных обмоток). Типовая схема системы
электроснабжения с асинхронными и синхронными двигателями, аналогичная
приведенной в [8], может быть представлена из питающих энергосистем С1 и С2 с
соответствующими ЭДС Е1, Е2, линий межсистемных связей Л1, Л2 и линии Л3,
подключенной глухой отпайкой к линиям Л1, Л2 для питания через понижающий
трансформатор Т двигательной и статической нагрузки на напряжении 6 — 10 кВ.
Трансформатор Т содержит две расщепленные обмотки низшего напряжения и имеет
схему соединений Υ/ Δ / Δ. В такой схеме будем рассматривать симметричные и
несимметричные короткие замыкания и кратковременные перерывы питания на стороне
высшего (110 — 330кВ) и низшего (6 — 10кВ) напряжений. Трёхфазная схема
замещения рассмотренной типовой схемы электроснабжения предоставлена на рис.2.
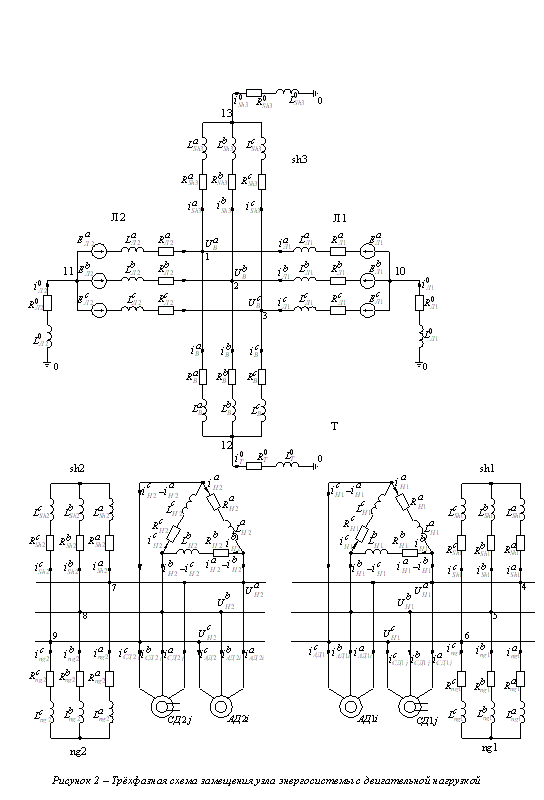
В этой схеме к каждой из секций 6 —
10 кВ подключены асинхронные (i=1,2…n) и синхронные двигатели (j=1,2…m),
статическая нагрузка ng1, ng2, шунты sh1, sh2 для моделирования коротких
замыканий, а также обмотки низшего напряжения трансформатора НН1 и НН2. Сеть
высшего напряжения представлена обмотками трансформатора, соединенными в звезду,
ЭДС систем ЕЛ1 и ЕЛ2, линиями Л1, Л2, шунтом sh3 для моделирования любых видов
коротких замыканий, а также заземлениями нейтралей питающих систем,
трансформатора Т и шунта sh3. Способы определения активных сопротивлений и
индуктивностей указанных элементов схемы рассмотрены в работах [2,8,11,12].
Асинхронные и синхронные двигатели представлены схемами замещений с
двухконтурным эквивалентным ротором по каждой из осей d, q и, кроме того, в
синхронных двигателях учтена обмотка возбуждения по оси d. Дифференциальные
уравнения статических элементов (трансформатора, питающих линий, шунтов,
нагрузки) записываются в фазных координатах а, b, c, o, уравнения асинхронных
двигателей - в неподвижных относительно статора координатах α, β, уравнения
синхронных двигателей — во вращающихся вместе с ротором каждой машины
индивидуальных осях d, q. При этом на каждом шаге расчета, используя
соотношения, приведенные в [12], производится преобразование переменных
асинхронных и синхронных двигателей к фазным координатам а, b, c. С целью
уменьшения количества вычислительных операций в данной модели за основу приняты
для асинхронных и синхронных двигателей дифференциальные уравнения, записанные
относительно токов статора и ротора [2,8]. Как видно из схемы замещения системы
(рис.2) она содержит кроме базисного нулевого 13 узлов, 34 ветви для статических
элементов, а также на каждой секции по n присоединений для асинхронных
двигателей и m присоединений для синхронных двигателей. Положительные
направления токов и напряжений ветвей указаны на схеме стрелками. Для
определения токов и напряжений ветвей за основу принят метод узловых напряжений.
Последние находятся из решения системы алгебраических линейных уравнений,
которая получена из выражений первого закона Кирхгофа для производных от узловых
токов. Для понижения порядка указанной системы уравнений с 13 до 9 выразим токи
в ветвях заземлений нейтралей через сумму соответствующих фазных токов и
определив через них напряжения узлов 10 — 13, учтём их затем в уравнениях
обмотки высшего напряжения трансформатора, линий Л1, Л2, шунта sh3. После
определения узловых напряжений переменные состояния находятся из численного
решения методом Рунге-Кутта дифференциальных уравнений отдельных элементов
схемы. Запишем дифференциальные уравнения отдельных элементов. Для
трёхобмоточного трансформатора имеющего расщеплённые обмотки низшего напряжения
с учетом рабочего магнитного потока и потоков рассеяния эти уравнения в
матричной форме записи в фазных координатах а, b, c, о могут быть представлены
как:
| Lва+Lт0 |
Lт0 |
Lт0 |
-Lm |
0 |
0 |
-Lm |
0 |
0 |
| Lт0 |
Lвb+Lт0 |
Lт0 |
0 |
-Lm |
0 |
0 |
-Lm |
0 |
| Lт0 |
Lт0 |
Lвc+Lт0 |
0 |
0 |
-Lm |
0 |
0 |
-Lm |
| -Lm |
0 |
0 |
LH1a |
0 |
0 |
Lm |
0 |
0 |
| 0 |
-Lm |
0 |
0 |
LH1b |
0 |
0 |
Lm |
0 |
| 0 |
0 |
-Lm |
0 |
0 |
LH1c |
0 |
0 |
Lm |
| -Lm |
0 |
0 |
Lm |
0 |
0 |
LH1a |
0 |
0 |
| 0 |
-Lm |
0 |
0 |
Lm |
0 |
0 |
LH2b |
0 |
| 0 |
0 |
-Lm |
0 |
0 |
Lm |
0 |
0 |
LH2c | |
· |
| piва |
| piвb |
| piвc |
| piH1а |
| piH1b |
| piH1c |
| piH2а |
| piH2b |
| piH2c | |
= |
| Uва -
iва(Rва +
Rт0) - iвb
Rт0 - iвc
Rт0 |
| Uвb -
iвb(Rвb +
Rт0) - iвa
Rт0 - iвc
Rт0 |
| Uвc -
iвc(Rвc +
Rт0) - iвa
Rт0 - iвb
Rт0 |
| (UH1c -
UH1a)/ √3 - RH1а
iH1а |
| (UH1a -
UH1b)/ √3 - RH1b
iH1b |
| (UH1b -
UH1c)/ √3 - RH1c
iH1c |
| (UH2c -
UH2a)/ √3 - RH2а
iH2а |
| UH2a -
UH2b)/ √3 - RH2b
iH2b |
| (UH2b -
UH2c)/ √3 - RH2c
iH2c | |
(1) |
В (1) используются параметры схемы
замещения трансформатора: Lm — индуктивность ветви намагничивания;
Rвa, Rвb, Rвc,
Rн1a, Rн1b,
Rн1c, Rн2a,
Rн2b, Rн2c — активные сопротивления
обмоток соответствующих фаз; Lвa,
Lвb, Lвc,
Lн1a, Lн1b,
Lн1c, Lн2a,
Lн2b, Lн2c - полные индуктивности
обмоток, состоящие из суммы индуктивностей рассеяния и индуктивности ветви
намагничивания; RТ0, RТ0 — активное
сопротивление и индуктивность для токов нулевой последовательности в цепи
заземления нейтрали обмоток высшего напряжения; p=d ⁄dt- оператор
дифференцирования. Дифференциальные уравнения
элементов сети высшего напряжения, шунта sh3 линий межузловых связей с их
питающими системами, имеющими заземлённые нейтрали, в фазной системе координат
a, b, c, о имеют вид:
| Lsh3а+Lsh30 |
Lsh30 |
Lsh30 |
| Lsh30 |
Lsh3b+Lsh30 |
Lsh30 |
| Lsh30 |
Lsh30 |
Lsh3c+Lsh30 | |
· |
|
= |
| Uва -
Rsh3а ish3а -
Rsh30(ish3a +
ish3b + ish3c) |
| Uвb -
Rsh3b ish3b -
Rsh30(ish3a +
ish3b + ish3c) |
| Uвc -
Rsh3c ish3c -
Rsh30(ish3a +
ish3b +
ish3c) | |
(2) |
| Lл0+Lл0 |
Lл0 |
Lл0 |
| Lл0 |
Lлb+Lл0 |
Lл0 |
| Lл0 |
Lл0 |
Lлc+Lл0 | |
· |
|
= |
| Eла -
Uва - Rла
iла -
Rл0(iлa +
iлb + iлc) |
| Eлb -
Uвb - Rлb
iлb -
Rл0(iлa +
iлb + iлc) |
| Eлc -
Uвc - Rлc
iлc -
Rл0(iлa +
iлb +
iлc) | |
(3) |
Для решения систем уравнений (1) —
(3) относительно производных токов необходимо найти обратные матрицы
индуктивностей трансформатора Lт-1, имеющую элементы
bmjт (m=1,…,9, j=1,…,9), шунта с элементами
bijsh3 (i=1,…,3, j=1,…,3), линий
Lл-1 с элементами bijл (i=1,…,3,
j=1,…,3, л=л1, л2 ), и умножить их на соответствующие правые части уравнений (1)
— (3). Тогда эти уравнения, приведенные к форме Коши, в фазной системе координат
примут следующий вид:
трансформатор:
pink=bm1tUвa+bm2tUвb+bm3tUвc+bm4t(UH1c-UH1a)/
√3 +
bm5t(UH1a-UH1b)/
√3 +
bm6t(UH1b-UH1c)/
√3 +
bm7t(UH2c-UH2a)/
√3 +
bm9t(UH2b-UH2c)/
√3 + bnkt, (4)
где
ankt= - bm1t
Rвa iвa - bm2t
Rвb iвb - bm3t
Rвc iвc -
Rт0(bm1t +
bm2t +
bm3t)(iвa +
iвb + iвc)Rвa
iвa - bm4t
RH1a iH1a -
bm5t RH1b iH1b
- bm6t RH1c
iH1c - bm7t
RH2a iH2a -
bm8t RH2b iH2b
- bm9t RH2c
iH2c
шунт sh3:
pish3k=
bi1sh3Uва +
bi2sh3Uвb +
bi3sh3Uвc +
aksh3, (5)
где
aksh3= - bi1sh3
Rsh3a ish3a -
bi2sh3 Rsh3b
ish3b - bi3sh3
Rsh3c ish3c -
Rsh30(bi1sh3 +
bi2sh3 +
bi3sh3)(ish3a +
ish3b + ish3c),
линии Л1, Л2:
piлk= -
bi1лUва -
bi2лUвb -
bi3лUвc + akл,
(6)
где
akл= bi1л
Eлa + bi2л Eлb
+ bi3л Eлc -
bi1л Rлa iлa -
bi2л Rлb iлb -
bi3л Rлc iлc-
Rл0(bi1л +
bi2л +
bi3л)(iлa +
iлb + iлc);
л=л1, л2
.
В (4) — (6) значение первого индекса в
обозначении элементов обратных матриц Lт-1,
Lsh3-1, Lл-1 определяются из
приведённой ниже таблицы, в которой индекс n соответствует обмоткам В, H1, H2, k
- фазам a, b, c, а индекс m определяется суммированием значений i и
l.
Таблица1. — Значения первого индекса в
элементах обратных матриц индуктивностей
| n |
B |
H1 |
H2 |
| k |
a |
b |
c |
a |
b |
c |
a |
b |
c |
| i |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
| l |
0 |
0 |
0 |
3 |
3 |
3 |
6 |
6 |
6 |
| m=i+l |
1 |
2 |
3 |
4 |
2 |
6 |
7 |
8 |
9 |
Дифференциальные
уравнения нагрузки ng1 и ng2, шунтов sh1 и sh2 на стороне низшего напряжения
трансформатора запишем в координатах a, b, c, в форме Коши аналогично [2]:
pizk=
bzkUHk + akz,
(7)
где:
bkz
= 1 ⁄ Lkz akz =
-bkzRzkizk;
Z=sh1, sh2, ng1, ng2; k=a, b, c; Н=Н1,
Н2.
Для синхронных двигателей из-за магнитной и
электрической несимметрии их роторов по осям наиболее целесообразно
дифференциальные уравнения решать в осях d, q ротора и осуществлять переход к
фазным координатам на каждом шаге расчёта. В [8] были получены полные
дифференциальные уравнения СД, имеющего кроме обмотки возбуждения по два
эквивалентных демпферных контура в осях d и q. Ниже приведём уравнения только
для производных токов статора pisd, pisq которые записаны в форме Коши во
вращающейся системе координат d и q:
pisd=-d11Rs isd -
d12Rrd'
ird'-d13Rrd"
ird"+d14(UF-Rf
if) + ω
d11(Lsqisq+(irq'+irq")Lmq)+d11Usd=TСДd+d11Usd;
(8)
pisq=-q11Rs isq -
q12Rrq'
irq'-q13Rrq"
irq"+d14(UF-Rf
if) - ω
q11(Lsdisd+(ird'+ird"
+
if)Lmd)+q11Usq=TСДq+q11Usq;
(9)
В уравнениях (8) и (9) используются
параметры схем замещения СД по осям d и q: Rs, Rf,
Rrd', Rrd",
Rrq', Rrq" — соответственно активные
сопротивления обмоток статора, возбуждения и демпферных контуров ротора;
Lmd, Lmq, Lsd, Lsq — индуктивности
ветвей намагничивания и полные индуктивности контуров статора; dij,
qij, — коэффициенты обратных матриц индуктивностей СД по осям d и q [
8 ]. Для определения выражений производных токов статора СД в осях a, b, c,
аналогично уравнениям статических элементов сети (4) — (7) воспользуемся
матрицами прямого ПСД и обратного ПСД-1
преобразования переменных и получим формулы для производных токов статора СД в
осях a, b, c и напряжений статора в осях d, q, которые потребуются нам в
дальнейшем:
| ПСД = |
cosγ |
-sinγ |
| cos(γ-2 π/3) |
-sin(γ-2 π/3) |
| cos(γ+2 π/3) |
-sin(γ+2 π/3) | |
| ПСД-1 =
2/3[ |
cosγ |
cos(γ-2 π/3) |
cos(γ+2 π/3) |
] |
| -sinγ |
-sin(γ+2 π/3) |
-sin(γ+2 π/3) | |
(10) |
|
|
=2/3 |
| cosγ |
cos(γ-2 π/3) |
cos(γ+2 π/3) |
| -sinγ |
-sin(γ+2 π/3) |
-sin(γ+2 π/3) |
|
|
; (11)
|
|
|
= |
| cosγ |
-sinγ |
| cos(γ-2 π/3) |
-sin(γ-2 π/3) |
| cos(γ+2 π/3) |
-sin(γ+2 π/3) |
| · |
| -ω · |
| sinγ |
cosγ |
| sin(γ-2 π/3) |
cos(γ-2 π/3) |
| sin(γ+2 π/3) |
cos(γ+2 π/3) |
| · |
| . (12)
|
Заменив в (12) производные для токов
СД их значениями из (8) и (9) с учётом (11), получим выражения для производных
токов статора СД в осях a, b, c:
piСДk =
b1kСД UHa +
b2kСД UHb +
b3kСД UHc +
akСД; (13)
где:
b1kСД =
2/3(d11cos(γ+θk)cos(γ) + q11sin(γ +
θk)sin(γ));
b2kСД =
2/3(d11cos(γ+θk)cos(γ - 2 π/3) + q11sin(γ +
θk)sin(γ - 2 π/3));
b3kСД =
2/3(d11cos(γ+θk)cos(γ + 2 π/3) + q11sin(γ +
θk)sin(γ + 2 π/3));
akСД =
(TСДd - ω isq)cos(γ) +
(TСДq + ω isd)sin(γ));
при k=a, θk =
θa = 0; при k=b, θk = θb = - 2 π/3; при k=c,
θk = θc = 2 π/3; Н = Н1,
Н2.
В [ 2 ] были получены дифференциальные
уравнения АД для двухконтурной схемы замещения, записанные в форме Коши в
неподвижной системе координат х, у. Выражения для производных токов статора при
этом имеют следующий вид:
pi
sx = -
k
11R
s i
x -
k
12R
r' i
rx' -
k
13R
r" i
rx" -
ω((k
12+k
13)L
m
i
sy+k
12L
r'
i
ry'+k
12L
m
i
ry'+k
13L
m
i
ry"+k
13L
r"
i
ry")+k
11U
sx=T
АДx+k
11U
sx;
(14)
pisy = -
k11Rs iy -
k12Rr' iry' -
k13Rr" iry" -
ω((k12+k13)Lm
isx+k12Lr'
irx'+k12Lm
irx'+k13Lm
irx"+k13Lr"
irx")+k11Usy=TАДy+k11Usy;
(15)
где: Rs,
Rr', Rr" — активные сопротивления
обмоток статора и демпферных контуров;
Lr',
Lr", Lm — полные индуктивности контуров ротора
и ветви намагничивания;
Lij — коэффициенты обратной матрицы
индуктивностей АД [ 2 ].
Для определения
выражений производных токов статора АД в осях a, b, c воспользуемся матрицами
прямого ПAД и обратного ПAД-1 преобразования
переменных и получим формулы для производных токов статора АД в осях a, b, c и
напряжений статора в осях х, у, которые потребуются нам в дальнейшем:
| ПAД = |
1 |
0 |
| -1/2 |
√3/2 |
| -1/2 |
-√3/2 | |
| ПAД-1 =
|
2/3 |
-1/3 |
-1/3 |
; (16) |
| 0 |
1/ √3 |
-1/
√3 | |
|
|
= |
| 2/3 |
-1/3 |
-1/3 |
| 0 |
1/ √3 |
-1/ √3 |
| · |
|
; (17)
|
Заменив в (18) производные для токов
статора АД их значениями из (14) и (15) с учётом (17) получим выражения для
производных токов статора АД в осях a, b, c:
piАДa =
b1АДUHa +
b2АДUHb +
b2АДUHc +
aaАД;
piАДb =
b2АДUHa +
b1АДUHb +
b2АДUHc +
abАД;
piАДc =
b2АДUHa +
b2АДUHb +
b1АДUHc +
acАД; (19)
где:
b1АД =
2/3 k11; b2АД = -1/3 k11;
aaАД = TАДx;
aaАД = -1/2TАДx +
√3/2TАДy; acАД =
-1/2TАДx - √3/2TАДy; H=H1,
H2.
Найдём выражения для расчёта узловых
напряжений в схеме. Для узлов расчётной схемы 1 — 9 согласно первому закону
Кирхгофа для производных токов имеем:
piBk +
pish3k - piЛ1k -
piЛ2k = 0; pish1k +
ping1k +
∑i=1СД1piСДik +
∑i=1AД1piAДik -
piH1k = 0;
pish2k +
ping2k +
∑i=1СД2piСДik +
∑i=1AД2piAДik -
piH2k = 0; (20)
где k=a, b,
c.
Подставив в (20) полученные ранее
выражения для производных токов из (4) — (7), (13) и (19) получим систему из
девяти алгебраических уравнений, записанную относительно неизвестных напряжений
в узлах расчётной схемы в системе неподвижных координат a, b,
c.
Таким образом получена математическая модель
типовой схемы электроснабжения (рис. 1), которая состоит из дифференциальных
уравнений её основных элементов и системы алгебраических уравнений для
определения узловых напряжений. На каждом шаге расчёта по предшествующим
значениям интегрируемых переменных определяются узловые напряжения, а затем,
одним из численных методов, выполняется шаг расчёта дифференциальных уравнений
всех элементов.
Расчёт режима заданного вида
короткого замыкания производится соответствующим изменением сопротивлений шунта
на время длительности короткого замыкания. После расчёта режима группового
выбега двигателей на короткое замыкание и восстановления до аварийных значений
шунта производится расчёт режима самозапуска двигателей. Моделирование режимов
группового выбега двигателей после отключения источника питания по причине, не
связанной с возникновением к. з., производится увеличением сопротивлений обмоток
высшего напряжения питающего трансформатора Т. При этом фиксируется величина,
частота и фаза напряжений на секциях, токи и мощности отдельных двигателей, что
позволяет оценить взаимообмен энергией и общий характер поведения узла
двигательной нагрузки. Моделирование режимов повторной подачи напряжения на
выбегающие двигатели позволяет определить возникающие значения токов и моментов
и дать оценку допустимости этих режимов в зависимости от фазы подаваемого
напряжения и успешности
самозапуска.
Преимущество разработанной модели
по сравнению с известными заключается в том, что она позволяет исследовать
поведение двигательной нагрузки при наиболее распространённых однофазных к. з. в
сети 110 — 330 кВ, а так же при обрывах проводов одной из
фаз.
ВЫВОДЫ
1.
Разработана математическая модель узла двигательной нагрузки энергосистем;
содержащая асинхронные и синхронные двигатели, статическую нагрузку и шунты для
моделирования симметричных и несимметричных коротких замыканий. Все элементы
узла описаны полными дифференциальными уравнениями и выражены относительно
производных токов.
2. Получены аналитические
выражения для определения на каждом шаге расчета мгновенных значений напряжения
в узлах расчета схемы.
3. Разработанная модель
позволяет анализировать режимы группового выбега и самозапуска, коротких
замыканий и другие переходные режимы узла комплексной нагрузки, содержащего
асинхронные и синхронные двигатели и может быть использована как на стадии
проектирования, так и эксплуатации узлов энергосистем, содержащих мощный
привод.
ЛИТЕРАТУРА
1.
Ойрех Я.А., Сивокобыленко В.Ф. Режимы самозапуска асинхронных двигателей. — М.:
Энергия, 1974. — 96 с.
2. Сивокобыленко В.Ф.,
Лебедев В.К., Кукуй К.А. Математическое моделирование асинхронной нагрузки в
режимах группового выбега и самозапуска. — Сб. научн. трудов ДонНТУ. Серия:
электротехника и энергетика, вып. 41: — Донецк: ДонНТУ, 2002. — с.
28-34.
3. Баков Ю.В. Проектирование
электрической части электростанций с применением ЭВМ: Учеб. пособие для вузов. —
М.: Энергоатомиздат, 1991. — 272 с.
4. Кетнер
К.К., Козлова И.А., Сендюрев В.М. Алгоритмизация расчетов переходных процессов
автономных электроэнергетических систем. — Рига: Зинатне, 1981. — 166
с.
5. Павлюк К., Беднарек С. Пуск и асинхронные
режимы синхронных двигателей. Пер. с польск. М., — Энергия, 1971. — 272
с.
6. Слодарж М.И. Режимы работы, релейная
защита и автоматика синхронных двигателей. — М.: Энергия, 1977. — 216
с.
7. Овчаренко А.С., Розинский Д.И. Повышение
эффективности электроснабжения промышленных предприятий. — К.: Техника, 1989. —
287 с.
8. Сивокобыленко В.Ф., Лебедев В.К.,
Кукуй К.А. Метод расчета группового выбега синхронной нагрузки электрических
систем. — Сб. научн. трудов ДонНТУ. Серия: электротехника и энергетика, вып. 50:
— Донецк: ДонНТУ, 2002. — с. 79-87.
9.
Сыромятников И.А. Режимы работы асинхронных и синхронных двигателей. — М.:
Энергоатомиздат, 1984. — 240 с.
10. Ковач К.П.
Переходные процессы в машинах переменного тока. — М.Л., Госэнергоиздат, 1963. —
744с.
11.Сивокобыленко В.Ф., Костенко В.И.
Математическое моделирование электродвигателей собственных нужд электрических
станций. — Донецк, ДПИ, 1979. — 110 с.
12.
Сивокобыленко В.Ф. Переходные процессы в многомашинных системах электроснабжения
электрических станций: Уч. пособие. — Донецк, ДПИ, 1984. — 116
с.
13. Голоднов Ю.М. Самозапуск
электродвигателей. — М.: Энергоатомиздат, 1985. — 136
с.
"Наукові праці Донецького технічного
універсітету". Серія: "Елктротехніка і енергетика", випуск 67. Донецьк: ДонНТУ,
2003. — 204 с.
Биография| Библиотека|
Реферат| Ссылки |Отчёт о поиске|
Индивидуальное задание
ДонНТУ
>Портал магистров ДонНТУ