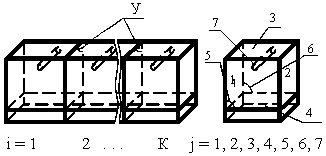
Рис. 1. Схема деления печи на зоны.
i - номер зоны, j - номер поверхности, У - условные поверхности
Известна [1] методика расчёта теплообмена в туннельной печи, базирующаяся на эмпирически полученных скоростях нагрева изделий. Расчёты получаются приближенными. Есть необходимость в создании более точной методики расчёта. В данной статье ставится задача разработки математической модели радиационного теплообмена в проходной электрической печи со стержневыми нагревателями на основе зонального метода с условными поверхностей (ЗУП) [2]. Метод ЗУП позволяет упростить систему нелинейных уравнений, описывающих лучистый теплообмен, и снизить объём вычислений по сравнению с классическим зональным методом [3]. Достоинства, недостатки, а также величина погрешности метода (ЗУП) рассмотрены в [4].
Будем решать задачу применительно к двухщелевой печи для обжига абразивных изделий с тремя ярусами стержневых электронагревателей. Для упрощения рассмотрим один ярус печи, где садка занимает всю поверхность пода (рис. 1).
Рабочее пространство печи (рис. 1) поделено на зоны условными поверхностями У. Каждая зона имеет 7 поверхностей: 1 и 2 - левая и правая торцевые, 3 - поверхность свода, 4 - поверхность изделия, 5 и 6 - поверхности боковых стен, 7 - нагреватель.
Система уравнений метода ЗУП записывается для объёмных зон. Плотность падающего теплового потока:
 ;
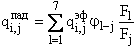i = 1, 2, 3, ... , К; j = 1, 2, 3, 4, 5, 6, 7. |
(1) |
Плотность эффективного излучения действительных поверхностей:
 ;
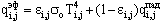i = 1, 2, 3, ... , К; j = 3, 4, 5, 6, 7; (1,1); (К,2). |
(2) |
Плотность эффективного излучения условных поверхностей:
 ;
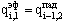i = 2, 3, ... , К; |
(3) |
 ;
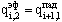i = 1, 2, ... , К-1; |
(4) |
Уравнение теплового баланса для поверхностей кладки:
 ;
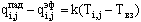i = 1, 2, 3, ... , К; j = 3, 5, 6; (1,1); (К,2) |
(5) |
Уравнение теплового баланса печи:
 |
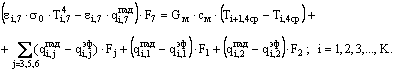(6) |
В уравнениях (1-6) обозначено: q - плотность теплового потока,
Вт/м2; Т - температура, К;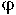 
- угловой коэффициент; 
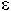- степень черноты; F - площадь поверхности, м2; k - коэффициент
теплопередачи через стенку печи, Вт/(м2К); Gм -
производительность печи, кг/с; см - теплоёмкость материала,
Дж/(кг°С); индексы: эф, пад - соответственно эффективный и падающий тепловые
потоки.
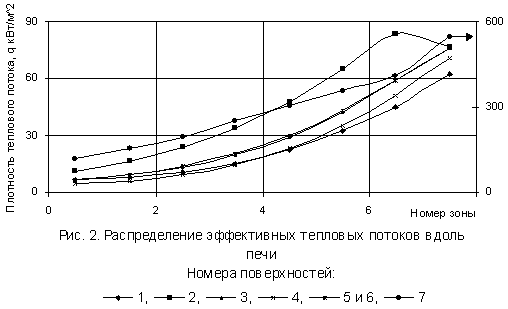
Разработаны алгоритм и программы расчёта при делении рабочего пространства печи на 4 и 8 зон. Нелинейная система уравнений (1-6) имеет соответственно 68 и 132 уравнения и решается методом Ньютона. На рис. 2 приведены распределения вдоль печи эффективных тепловых потоков всех поверхностей для 8 зон.
В ходе расчётов на ПК было выполнено 5-7 итераций менее чем за секунду. Исходными данными для расчётов были график обжига изделий, производительность печи, геометрические размеры рабочего пространства и теплофизические свойства материалов.
По результатам расчётов можно сделать вывод, что если распределения температур носят монотонный характер, то эффективный тепловой поток с условной поверхности 2 имеет максимум в предпоследней зоне (рис. 2). Вероятно это связано с влиянием близко расположенной торцевой стенки печи.
