Коноплёва Анна Петровна
Факультет: Вычислительная Техника и Информатика (ФВТИ)
Специальность: Системное Программирование (СП)
Тема выпускной работы: "Разработка и исследование программных средств для работы с гипекодами"
Научный руководитель: Аноприенко Александр Яковлевич
АВТОРЕФЕРАТ
1. Когнитивное моделирование. Что это такое. Области применения. Перспективы развития
1. 1. Иллюстративноя и когнитивнаяфункции компьютерной графики и когнитивного компьютерного моделирования
В настоящее время
компьютерная графика (КГ) - это одно из наиболее бурно развивающихся
направлений информационных технологий. В современных научных исследованиях, в
том числе и в фундаментальных, компьютерная графика стала комплексным
познавательным инструментом - массовым атрибутом современного образовательного
процесса и научных исследований.
В начале функция КГ была
исключительно иллюстративной. Однако, с развитием этого направления, все
большее значение приобрели те возможности КГ, которые позволяют активизировать
свойственную человеку способность мыслить сложными пространственными образами. Это,
так называемая когнитивная функция КГ.
Иллюстративная функция КГ
сводится к воплощению в том или ином визуальном оформлении то, что уже
известно, т. е. существует в окружающем нас мире либо как идея в голове
исследователя. Когнитивная же функция состоит в том, чтобы с помощью некоторого
изображения - модели получить не
существующее еще даже в голове специалиста знание, способствовать интеллектуальному процессу
получения этого знания.[6]
За тот период истории
существования компьютерной когнитивной графики (ККГ) сформировалась
определенная классификация основных ее направлений:
- первое направление занимается теми
областями, где задача вербализируема, но не решаема или трудно решаема без
применения некоторых нетрадиционных методов, например, экспертных систем;
-
второе направление - моделирование когнитивных процессов, связанных с
пониманием и обработкой
текстово-графической информации, т.е. разработка систем типа “Текст - рисунок”
и “Рисунок - текст”;
- третье направление ККГ - "системы"
восприятия и оценки” - во многом сходно с первым. Однако, здесь критична не
столько сложность задачи, сколько объем исходной информации и время, дающееся
на принятие решения [7].
Для уменьшения
времени, необходимого для восприятия той или иной информации, при ее
предъявлении имеет смысл обращаться не столько к мало-производительному "механизму" логики, сколько к более мощному – интуитивно ассоциативному
мышлению.
Например,
информация, представленная в виде изменения формы, цвета фигуры, искажение ее
пропорций, воспринимается гораздо быстрее, чем та же информация в текстовом
виде [7].
В настоящее время наряду
с традиционным компьютерным моделированием КГ стала частью перспективного
направления информационных технологий когнитивного компьютерного моделирования (ККМ) [2].
Моделирование реальных
когнитивных процессов всегда находилось в центре когнитивистских исследований.
Расширившиеся возможности современных компьютеров позволяют, с одной стороны,
рассчитывать на построение адекватных моделей когнитивных процессов, а с другой
стороны, использовать идеи и методы когнитивных наук при решении практических
задач. Можно полагать, что когнитивное моделирование, вобрав в себя достижения
нейронаук, лингвистики, инженерии знаний, психологии и других когнитивных наук, явится ключем к созданию интеллектуальных систем нового поколения [2].
1.2. Психологические аспекты
эффективности применения ККМ в развитии интуитивно ассоциативного мышления
«Понятия без чувств пусты, впрочем,
также как
чувства без понятий слепы
Эммануил
Кант.
ККМ опирается
исключительно на способности человеческого разума к мышлению, которое состоит
из 6 основных операций: анализ, сравнение, обобщение, синтез, абстрагирование,
конкретизация.
В результате этих 6-ти
операций в сознании человека на основе сенсорной информации (зрительной,
слуховой, тактильной и т. д.) рождаются определенные теоретические и
практические выводы. Это дает нам новую оценку и пути улучшения того, что мы
воспринимаем.
Из всех познавательных
процессов мышление занимает особое, уникальное место. Именно мышление всегда связано с
постановкой, формулированием и поиском путей решения любой задачи ( в этом
смысле мышление – исключительно активный процесс, оно не может быть
непроизвольным, пассивным).
Мышление не существует
как абстрактный, отдельный, совершенно самостоятельный процесс в том смысле,
что оно сопровождается восприятием (делая его целостным и избирательным), запоминанием (делая его
долговременным, смысловым), без него не возможно развитие воображения.
Именно мышление позволяет
перейти от незнания к знанию, от неумения к умению, от отсутствия навыка к его
наличию. Отсюда логически вытекает заключение: чем выше уровень мышления, тем
выше результаты всех познавательных процессов, а значит, и потенциальных возможностей роста интеллекта.
Поскольку мышление
направлено на добывание качественных теоретических знаний и их практическое
использование, без него не имеет смысла ни восприятие, ни запоминание. Именно
поэтому основной целью ККМ становится не только красиво, наглядно и как можно
более информативно отобразить сложные процессы, а помочь в осмысленном восприятии целостного образа,
сделать его нестатичным, постоянно изменяющимся, помочь найти в нем
новые черты, оттенки, что способствует поиску рационального решения все новых и
новых задач.
1.3. Задачи компьютерной когнитивной графики
Первой задачей является созданиетаких моделей представления знаний, в которых была бы возможность однообразными
средствами представлять как объекты, характерные для логического мышления, так
и образы-картины, с которыми оперирует образное мышление.
Вторая задача - визуализация тех
человеческих знаний, для которых пока невозможно подобрать текстовые описания.
Третья - поиск путей перехода от
наблюдаемых образов-картин к формулировке некоторой гипотезы о тех механизмах и
процессах, которые скрыты за динамикой наблюдаемых картин.
Эти три задачи ККГ с
позиций информационных технологий поддержки принятия решений следует дополнить
четвертой задачей. Она заключается в создании условий для развития
профессионально-ориентированных интуиции и творческих способностей путем
построения пользовательского интерфейса, основанного на методах когнитивной
графики.
При разработке
компьютерных информационных систем анализа состояния объекта контроля и управления
обычно исходят из первых двух задач когнитивной графики, когда знания о
техническом объекте, полученные в ходе исследований и проектирования
пользовательского интерфейса представляются в привычной символьно-цифровой
форме. Множество таких данных делают их недоступными для анализа человеком. Четкое осознание третьей
и четвертой задач когнитивной графики позволяет формулировать дополнительные
требования как к собственно графическим изображениям, так и к соответствующему
программно-методическому обеспечению. Среди них можно выделить:
- адекватность изучаемым объектам или
процессам, используемым инженерным методам и методикам обучения;
-естественность и доступность для
восприятия пользователями;
-удобство для анализа качественных
закономерностей распределения параметров;
-эстетическую привлекательность,
быстроту формирования изображения.
Бурное
развитие средств вычислительной техники и огромное разнообразие программных
продуктов открывают новые возможности для создания современного
пользовательского интерфейса. Новые средства ввода, вывода, передачи, хранения
и преобразования информации позволяют использовать речевой ввод и вывод,
виртуальную реальность, мультипликационные и видео-образы, чертежи, карты,
сложные трехмерные динамические графические образы и т.п., что существенно
расширяет "полосу пропускания" информации при общении человека с
компьютером.
Проектировщикам желательно
выбирать подходящие формы графических изображений, вносить игровые и
исследовательские компоненты в исследовательскую работу, естественным образом
побуждая пользователя к глубокому и всестороннему анализу свойств изучаемых
объектов и процессов [8].
2.ФОРМЫ ПРЕДСТАВЛЕНИЯ ГИПЕРКОДОВ
2.1. Современные разработки в области многозначной логики
Современные
информационные технологии практически полностью базируются на двоичной логике — то есть, все вычисления
производятся на уровне нулей и
единиц. Двоичная логика компьютеров — естественное следствие
физических особенностей полупроводников. Единица
(обозначающая заряд) и ноль (обозначающая, что транзистор не пропускает
тока) — в настоящее время это основа всех вычислительных процессов вкомпьютерах и прочих "умных" устройствах [1].
Однако, в условиях сетевой
параллельности проявились недостатки традиционной булевой логики. На данном
этапе они компенсируются за счет алгоритмично-программного аппарата. Но, несмотря
на то, что таким образом достигается
универсальность современных компьютерных систем, это приводит к снижению
продуктивности на несколько порядков в сравнении с аппаратной поддержкойподобных функций [1].
Одним из
вариантов усовершенствования традиционной двоичной логики является переход к
многозначной логике [1].
2.2 Троичная логика. Перспективы
внедрения в компьютерные технологии.
Реализацией
аппаратных устройств, основанных на многозначной логике заинтересовались разработчики технологий для
беспроводных коммуникаций International
Technology Roadmap for Semiconductors (ITRC).На
данном этапе это становится
возможным. Разработчики заинтересовались новыми
"экзотическими" сплавами, такими как кремний-германий (SiGe),
что могло бы обеспечить тактовую частоту беспроводных устройств до
100 ГГц [3].
В транзисторе
из SiGe можно создавать несколько пороговых уровней напряжения, а это означает совместимость
с многозначной логикой – с одной стороны, большая ресурсоёмкость – с другой. По
подсчетам специалистов 16-битный микрокомпьютер, основанный на двоичной логике,
обладает памятью не более 216 (65 тысяч)
битов, в то время как при использовании троичной логики, объём памяти мог
бы возрасти до 43 миллионов битов (316 битов) [3].
В своё
время производители микросхем уже пытались перейти на троичную логику.
Но возникли множественные проблемы, связанные с недостаточным
развитием технологий в то время. Вследствие использование
однородных кремниевых структур, многозначность логики приходилось
обеспечивать с помощью двоичных "логических вентилей". Какие-то
решения подобного рода выпустили на рынок
;в итоге и Intel, и Fairchild, а с ними National
Semiconductor, Signetics (теперь Philips) и Motorola.
Их продукция базировалась на троичной и даже
четвертичной логике [3].
Недостаточный
уровень развития производственных технологий на том этапе, впрочем, привёл к
тому, что двоичные устройства оказались более выгодными с экономической точки
зрения [3].
Однако,
возможность и целесообразность перехода производителей полупроводников к
многозначной логике подчеркивается в статье известного в США
IT-консультанта
Бернарда Коула:"Мы уже возвращаемся к некоторым старым идеям,
выброшенным в мусорную корзину истории, — такие, как кремний-на-изоляторе,
асинхронная логика, ферро-электрическая память и кремниево-германиевые сплавы.
Почему бы не вспомнить и про многозначную логику?" [3]
2.3 Тетралогика
Тетралогика
(четырехзначная логика) также, как и троичная логика является частным случаем многозначной логики. Включает кроме
классических 1 («истина») и 0 («ложь») разные пары комбинаций следующих
значений:
- M как "множественность"
- А как "возможность","равно вероятность"
- и некоторые
другие. (Интересные варианты приведены в [8]).
На основе тетралогики
вводится понятие тетракода, которое представляет собой расширение обычного
бинарного кода. Каждый разряд тетракода представляет собой двухбитную
комбинацию, которая соответствует одному из четырех состояний тетралогики.
Таким образом суммарное количество бит для представления числа увеличивается в
2 раза, но при этом осуществляется качественно важное изменение кода: из
точечного числа он превращается в одномерное, что эффективно использует все
пространство числовой оси [1],[8].
Наличие хотя бы в одном
разряде значения М приведет к множественности значения. Например
1111 111M = {1111 1110; 1111 1111}
Тетракоды являются высоко
эффективными объектами, которые позволяют выйти за границы традиционной
компьютерной бинарной логики. И дают возможность приблизить компьютерную логику
к логике, свойственной человеку.
3.ВИЗУАЛИЗАЦИЯ ГИПЕРКОДОВ МЕТОДАМИ КОГНИТИВНОГО МОДЕЛИРОВАНИЯ
3.1. Актуальность развития идеи многозначной логики
Когнитивное моделирование
в контексте данной работы является инструментом для визуализации идеи о
гиперкодах, как об эволюционно новой форме представления кодо-логического
базиса, которая является скорее абстрактным понятием на данном этапе своего развития.
Существуют определенные
предпосылки для дальнейшего развития этого понятия.
Многозначная логика на
данном этапе развития человечества входит в спектр тех задач, которым
необходимо решение. Развитие этого направления может существенно расширить возможности
компьютерной техники, открыть большие возможности для создания искусственного интеллекта, послужить основой
для усовершенствования молекулярной биологии, генетики, химии, физики,
математики и многих других фундаментальных наук.
3.2. Визуализация «карт
Карно» как частного случая представления гиперкодов
Как уже было сказано
выше, двоичный код является частным случаем многозначной логики. Одной из
традиционных форм его представления являются "карты Карно" [4].
Если рассматривать "карты
Карно" в контексте многомерного логического пространства, можно выделить такие основные значения, которыми оперируют при работе с ними:
1 - TRUE (значение "истина");
0 – FALSE (значение"ложь");
* - безразличие к значению TRUE или FALSE.
"*" может
рассматриваться как еще одно, дополнительное логическое значения [4].
В рамках этой работы был разработан интерфейс для работы с "картами Карно". Был
реализован алгоритм "склейки" "карт
Карно" размерностью 4*4 для четырех переменных в двоичном коде. В ходе
дальнейшей работы планируется реализовать этот алгоритм для любой размерности и
любого числа переменных.
Среда
программирования ActionScript на базе Macromedia Flash MX.
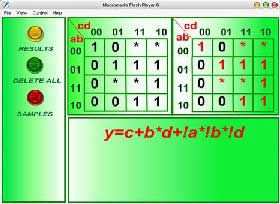
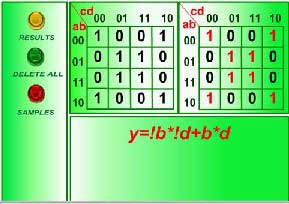
Пример работы программы приведен на рисунке 3.1.
|
Пример №1
|
Пример №2
|
|
|
|
Рисунок 3.1 - Реализация алгоритма "склейки карт Карно"
Такая интерактивная
программа может стать частью большого проекта, например книги по дисциплине "Прикладная теория
цифровых автоматов", в которой наряду с традиционными текстовыми пояснениями
могут приводиться разноплановые развивающие обучающие пособия такого типа [4].
Кроме того, такая
программа является визуализацией простейших гиперкодов, а потому может
послужить примером программного средства для работы в многомерном логическом
пространстве.
В рамках магистерской
работы разрабатывается подобная программа для работы с более сложным
кодо-логическим базисом.
3.3. Модель
отображения гиперчисел
Для того, чтобы решить ту
или иную научную задачу, нужно сначала представить, как могут выглядеть ее
решения. Из множества решений выбрать оптимальное. В случае с гиперкодами,
необходимо продумать множество вариантов их визуализации и выбрать из них самые
понятные и наиболее информационные [5].
Человечество еще в
далеком прошлом нашло способ визуализации монокодов – простые счетные палочки,
с задачей визуализации дикодов уже справились – временные диаграммы, а для
гиперкодов пока нет графических аналогов [1].
Итак, следующим этапом
данной работы был поиск способов визуализации гиперкодов на числовых осях х, у.
Разработана программа, входными данными которой являются два числа (2
координаты). Если бы речь шла об обычных числах, то результатом работы такой
программы была бы обычная точка координатной плоскости.
Случай с гиперкодами
более сложен. Здесь результатом должен быть диапазон гиперчисел. Поскольку
гиперчисло может быть определено как диапазон, то и отображать следует уже
диапазон диапазонов, где каждое гиперчисло может пересекаться с другим, в то же
самое время все диапазоны должны быть разными [5].
Работа в этом направленииеще ведется, но предварительным результатом может быть приведенная на рисунке 3.2. таблица.
Как видно из рисунка 3.2 гиперчисла могут находиться в различных соотношениях друг с другом в
зависимости от координат.
|
Диапазон гиперчисел с координатами 50\50
|
Диапазон гиперчисел с координатами 20\20
|
 |
 |
Рисунок 3.2 - первый предлагаемый способ визуализации гиперкодов
Следующим этапом работы стало интерактивное приложение, входными данными которого служит 4-разрядное
число в формате гиперкода. В зависимости от введенного значения на экране
генерируется его визуальное отображение на координатной плоскости.
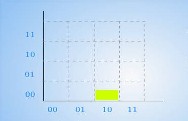
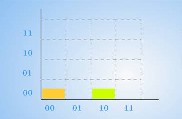
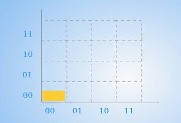
Результаты работы этой программы, которые довольно исчерпывающего объясняют принцип гиперкода, приведены на рисунке 3.3. Это еще один из способ визуализации гиперчисел.
|
Входные данные
|
Выходные результаты
|
Входные данные
|
Выходные результаты
|
|
0010
|
|
00М0
|
|
|
00А0
|
|
00А0
|

|
|
ММММ
|

|
|
|
Рисунок 3.3 - второй предлагаемый способ визуализации гиперкодов
ЛИТЕРАТУРА
[1] Аноприенко А.Я. Тетралогика и тетракоды. / В кн. “Сборник трудов факультета вычислительной техники и
информатики”. Вып.1. Донецк, ДонГТУ, 1996.
[2] Аноприенко А.Я. От вычислений к пониманию: когнитивное компью-терное моделирование и опыт его практического применения на при-мере решения проблемы Фестского диска // Научные труды Донецкого государственного технического университета. Выпуск 6. Серия "Ин-форматика, кибернетика и вычислительная техника" (ИКВТ-99). – До-нецк: ДонГТУ. – 1999. – С. 36-47
[3] Bernard Cole "Is it time to move beyond zeroes and ones?" //URL: Embedded.com
[4] Коноплева А. П. Аноприенко А.Я.
"Применение интерактивных приложений на Flash MX в дисциплине ПТЦА"
//Тезисы доклада на научную конференцию студентов, аспирантов и молодых ученых «КОМПЬЮТЕРНЫЙ МОНИТОРИНГ И ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ», ДонНТУ, май 2006 г.
[5] Коноплева А. П. Аноприенко А.Я.
"Задачи когнитивного компьютерного моделирования и его практическое применение для визуализации гиперкодов"//Тезисы доклада на научную конференцию студентов, аспирантов и молодых ученых «КОМПЬЮТЕРНЫЙ МОНИТОРИНГ И ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ», СевНТУ, апрель 2007 г.
[6] Дж. Лакофф Когнитивное моделирование// Язык и интеллект. - М.: Из-дательская группа “Прогресс”. – 1996. – C. 143 – 182.
[7] ЗенкинА.А, .ЗенкинА.А., Когнитивная Реальность:Порождение Творческих Решений В Науке, Образовании, Управлении. //Труды Международной конференции "Пользовательский интерфейс в современных компьютерных системах". - Орел, Россия, 1999
[8]Соболева А.Г. Когнитивная визуализация данных с помощью лиц Чернова // Збірка тез доповідей II Міжнародної наукової конференції студентів, аспірантів та молодих вчених “Комп’ютерний моніторинг та інформаційні технології 2006”, 15-17 травня 2006 р. – Донецьк: ДонН-ТУ, 2006. – С. 135-136.








