
Источник http://www.info.donntu.ru/el_izdan/geolog/sborniki/ggf111t2.pdf
Вернуться в библиотеку Сагайдак Д. И., ДонНТУ
ПОСТАНОВКА ЗАДАЧИ
Применение цифровых фотокамер для стереофотограмметрической съемки невозможно без их периодической калибровки [1]. В процессе ее выполнения контролируются и при необходимости корректируются элементы внутреннего ориентирования фотокамер. Метод калибровки с помощью тестового полигона является наиболее распространенным и легко реализуемым на практике [2, 3]. Несмотря на это до настоящего времени не сформулированы оптимальные параметры калибровки камеры по тестовому полигону. Под параметрами калибровки понимают характеристики тест-объекта (габариты, форма, количество опорных точек), взаимное расположение тест-объекта и камеры (удаление, угол фотографирования), количество снимков. Из опубликованных работ по калибровке камер с помощью тест-объекта, касающихся формируемой проблемы, необходимо выделить работу проф. Дубиновского [1]. В ней в качестве исследуемых параметров рассматривались превышения между опорными точками полигона используемого для калибровки. Было получено, что для полной калибровки нормальноугольной камеры по пространственному (рельефному) полигону превышения между опорными точками должны составлять не менее половины высоты фотографирования. При выполнении калибровки с помощью плоского тест-объекта, по утверждению автора работы [1], необходимо использовать конвергентный случай съемки. Исследование влияния значения угла конвергенции на точность решения задачи калибровки в работе не выполнялось. В работах других авторов [4-8] решение задачи калибровки с необходимой точностью достигалось путем вывода новых математических зависимостей и алгоритмов.
ЦЕЛЬ ИССЛЕДОВАНИЙ
Определение оптимальных параметров калибровки камеры с помощью плоского тестового полигона, то есть выбор оптимальных условий фотографирования и параметров полигона, при которых решение задачи калибровки выполняется с наивысшей возможной точностью.
МЕТОД РЕШЕНИЯ
Поиск оптимальных параметров выполнен методом моделирования съемки тестового полигона. На основании известных координат тестового полигона и элементов внутреннего и внешнего ориентирования снимка рассчитывались координаты на снимке. Полученные макетные снимки рассматривались как результаты измерений реальных снимков с неизвестными элементами ориентирования. Решение задачи калибровки выполнялось на основании уравнений коллинеарности, параметрические уравнения которых совместно с систематическими ошибками в общем случае согласно [9] имеют вид

где vxi,j, vyi,j - поправки в измеренные координаты точки i на снимке j;
aj1, bj1...cj3- направляющие
косинусы системы координат фотокамеры для j-го снимка;
Xi, Yi, Zi - геодезические координаты
точки местности;
Xjs, Yjs, Zjs - геодезические
координаты точки фотографирования j - го снимка;
x0, y0, f - соответственно
координаты главной точки и фокусное расстояние;
xi,j, yi,j - координаты изображения
точки i на снимке j;
jx(xi,j, yi,j, w11, w12...w2k),
jy(xi,j, yi,j, w11, w12...w2k) - функции,
описывающие систематические ошибки в измеренные координаты соответственно по
xi,j, yi,j .
После разложения уравнений коллинеарности (1) в ряд вокруг приближенных значений определяемых величин и объединения однородных частных производных в матрицы получаем линейное уравнение поправок для точки:
vi,j=di,j×dWj+fi,j+ dc+si,j×dw+li,j (2)
где dW
j, dc,
dw
- векторы поправок, соответственно, в элементы внешнего и
внутреннего ориентирования снимка j, а также в параметры систематических ошибок
координат точек; Объединив уравнения (2) для точек одного снимка в одноименные матрицы
получаем выражение: Dj×dWj+
Fj×dc+
Sj×dW+
Lj
(3) где обозначения аналогичны формуле (2). Совокупность уравнений (3) формирует систему параметрических уравнений
коллинеарности, которую можно записать как: где n - количество снимков, используемых для калибровки. Решая систему уравнений (4) методом наименьших квадратов при выполнении
условия VVт=min (5) получаем При решении задачи калибровки для снимков не искаженных за влияние
дисторсии объектива из уравнений (6) исключаются соответствующие неизвестные
dW. Используя метод исключения Гаусса систему
уравнений (6) разрешаем относительно вектора dc:
Вводя соответствующие обозначения, получаем выражение: dc=-N-1×L (8) Для характеристики точности калибровки служат диагональные элементы
матрицы N-1, выражающие величины обратные весам определения элементов
внутреннего ориентирования (ЭВО): Среднеквадратическая ошибка определения фокусного расстояния выражается
формулой где m- точность измерения координат
точек на снимках. Для координат главной точки выражение (10) будет аналогичным. УСЛОВИЯ ЭКСПЕРИМЕНТА Моделирование выполнялось для цифровых камер,
относящихся к классу узкоугольных. Прототипом являлась цифровая
пятимегапиксельная камера Olympus E20P с углом поля зрения от 14o
до 50o. Координаты опорных точек рассчитывались из условия, что калибровочный полигон
представляет собой плоскость. Возможные варианты параметров фотографирования, которые определяют
положение камер относительно тестового полигона, показаны на рисунке 1. Рис. 1. Параметры фотографирования Схема фотографирования тестового полигона представлена для одной
стереопары. Можно выделить две совокупности параметров определения
местоположения камеры относительно тестового полигона при фиксированном
значении фокусного расстояния камеры и размерах снимка:
di,j, fi,j, si,j - матрицы
частных производных по соответствующим переменным;
li,j- вектор свободных членов.
 (4)
(4) (6)
(6)  (7)
(7) (9)
(9) (10)
(10)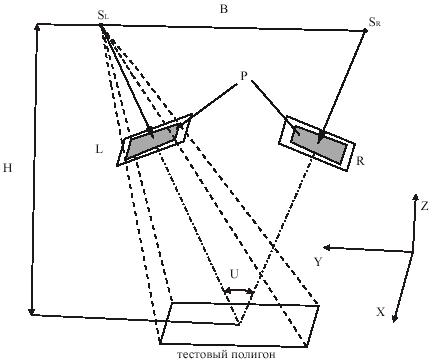
Под величиной P понимается процентное отношение площади фигуры, полученной путем оконтуривания изображения на снимке, к площади всего снимка. Очевидно, что при выполнении съемки с целью дальнейшей калибровки камеры значение площади заполнения на снимках должно быть максимально возможным. При условии выполнении этого условия для обеих групп параметров, количество величин для исследования сокращается. В первой совокупности остаются высота и базис фотографирования, а во второй – угол конвергенции. Для исследования была выбрана вторая группа параметров, что объясняется меньшим количеством величин и известным диапазоном их изменения.
В качестве дополнительных параметров фотографирования (условий фотографирования) могут использоваться количество снимков и количество точек тестового полигона. Эти параметры не определяют геометрическое место камер, но их регулирование может повлиять на точность решения задачи калибровки. Подробнее эти параметры рассмотрены ниже.
ОТСТОЯНИЕ СЪЕМКИ
Для подтверждения верности выбранных параметров, определяющих решения задачи калибровки, был проделан следующий эксперимент. При постоянном угле конвергенции стереопар было смоделировано фотографирование полигона на разных отстояниях. При этом площадь заполнения оставалась постоянной, что достигалось увеличением расстояния между опорными точками полигона. В результате расчетов точность определения элементов внутреннего ориентирования для моделей съемок, выполненных с различных отстояний, осталась постоянной. Это свидетельствует о том, что при неизменных значении площади заполнения снимка и угле конвергенции, изменение высоты фотографирования не влияет на точности решения задачи калибровки.
УГОЛ КОНВЕРГЕНЦИИ
Угол конвергенции. Исследования значений этого параметра выполнялось при разных углах поля зрения камеры. Угол поля зрения камеры (УПЗ) выражается градусной мере независимо от единиц измерения элементов внутреннего ориентирования. Для каждого из исследуемых УПЗ рассчитывалась модель при возможных углах конвергенции стереопар. Площадь покрытия при построении моделей всегда оставалась максимально возможной независимо от угла наклона камеры. На рисунке 2 и 3 изображены графики изменения точности определения соответственно фокусного расстояния и координат главной точки камеры зависимости от угла конвергенции стереопар. Ввиду незначительной разницы графики изменения весовых значений по x0 и y0 усреднены между собой для каждого УПЗ.
Для пояснения величин, изображенных на рисунках обратимся к выражению (11), которое выражает значения матрицы весовых коэффициентов (9) для минимума графика на рисунке 2 соответствующего УПЗ = 14o
 (11)
(11)
На основании (10) значение вектора среднеквадратических ошибок для (11) примет вид
 (12)
(12)
Значения вектора (12) показаны на рисунках 2 и 3 крестами.
Для шкал на рисунках 2 и 3 введем соответствующее обозначение:
 (13)
(13)
Как показывают рисунки, увеличение УПЗ камеры ведет к увеличению значения оптимального угла конвергенции стереопар. Точность решения задачи калибровки при этом увеличивается.
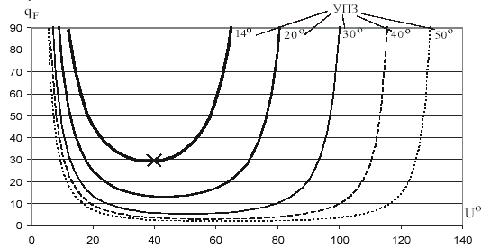
Рис. 2. Точность определения фокусного расстояния камер в зависимости от угла конвергенции стереопар
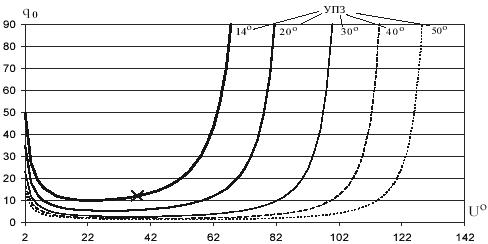
Рис. 3. Точность определения координат главной точки снимка в зависимости от угла конвергенции стереопар
Кривые, построенные для камер с большим углом поля зрения, имеют так называемое «плоское дно». Это говорит о том, что соблюдение оптимального угла конвергенции для широкоугольных камер не так строго, как для узкоугольных. Из рисунка 2 видно, что отклонение угла конвергенции стереопар от минимума функции для УПЗ=50o на 15o практически не изменит точность решения задачи калибровки. Такое же отклонение для камеры с УПЗ=14o значительно ухудшит точность решения задачи калибровки.
Следует отметить, что оптимальные углы конвергенции найденные соответственно по рисункам 2 и 3 отличаются между собой. Конечным значением оптимального угла конвергенции для данного УПЗ принимается угол, найденный из условия наивысшей возможной точности определения фокусного расстояния. Наличие плоского дна в графиках на рисунке 3 дает возможность изменения угла конвергенции без значительной потери точности определения координат главной точки.
Изложенные результаты получены для моделей со следующими параметрами: 8 симметрично расположенных относительно полигона снимков, 48 опорных точек, средняя площадь проекции полигона на снимках не менее 60%.
ПЛОЩАДЬ ПОКРЫТИЯ
Найденные значения оптимальных углов конвергенции для камер с разными УПЗ были получены при моделировании с максимальной площадью покрытия. Очевидно, что несоблюдение этого принципа приведет к потере точности решения задачи калибровки.
Для оценки влияния площади покрытия был выполнен такой эксперимент. Путем моделирования для камеры с УПЗ=14o строились макетные снимки с различной площадью покрытия. Значение угла конвергенции было выбрано по графику на рисунке 2. Изменение площади достигалось путем приближения и удаления камеры от тестового полигона по направлению оси фотографирования. Проведенные эксперименты показывают, что уменьшение площади покрытия с 70% до 25% приводит к уменьшению точности решения задачи калибровки в три раза.
КОЛИЧЕСТВО СНИМКОВ И ТОЧЕК ТЕСТОВОГО ПОЛИГОНА
Количество снимков и точек тестового полигона: Принципиальное решение задачи калибровки на основании уравнений коллинеарности возможно при наличии одной стереопары (двух снимков) и четырех опорных точек тестового полигона. В этом случае имеется 15 неизвестных, в том числе 6 элементов внешнего ориентирования для каждого снимка и 3 элемента внутреннего ориентирования для камеры. Для 4-х опорных точек можно составить 16 уравнений коллинеарности (по 8 на каждом снимке) и выполнить решение по МНК. Утверждение справедливо без поиска коэффициентов полинома дисторсии. Следовательно, увеличение количества снимков и точек тестового полигона приводят к избыточным измерениям и улучшают процесс решения задачи калибровки. На рисунке 2 показан пример, в котором достигнут наилучший результат решения, исходя из геометрического местоположения точек фотографирования относительно тестового полигона. Результат получен выбором оптимального угла конвергенции и максимальной площади покрытия снимка. Дальнейшие изменения положения камер не приведут к улучшению точности. Получить лучшее решение возможно при увеличении одного из указанных параметров (количество снимков или количество точек).
Для узкоугольной камеры (с УПЗ=14o) был проведен эксперимент при оптимальном угле конвергенции, максимальной площади покрытия и разных количествах точек тестового полигона (48 и 192 шт.). В результате, увеличения количества точек в четыре раза привело к повышению точности решения в два раза.
Для количества снимков выполняется тоже условие. Отличие между этими параметрами состоит в том, что изменение количества точек обеспечить достаточно сложно. Процесс калибровки камеры выполняется при построенном тестовом полигоне, а добавление точек приведет к дополнительным затратам на монтаж и геодезические работы по определению координат. Добавление снимков приведет только к увеличению затрат на этапе измерений координат точек на изображениях. В качестве дополнительных снимков могут использоваться снимки, выполненные с тех же точек фотографирования, но с поворотом камеры в плоскости перпендикулярной оси съемки [6].
В процессе решения необходимо оптимально подбирать количество точек и снимков тестового полигона. С одной стороны добавление этих параметров приведет к увеличению точности решения задачи калибровки, а с другой – к увеличению времени измерений и расчета.
Все выполненные эксперименты по выбору оптимального местоположения камеры относительно тестового полигона выполнялись для макетных снимков, смоделированных без учета дисторсии объектива. При уравнивании снимков, в координатах которых присутствуют систематические ошибки, вызванные дисторсией объектива, в математической модели калибровки необходимо добавлять дополнительные неизвестные (1). Задача совместного нахождения элементов внутреннего ориентирования и коэффициентов систематических ошибок относится к некорректным по Тихонову [10]. Детально этот вопрос будет рассмотрен в следующей работе.
ВЫВОДЫ
В работе обоснованы и определены параметры калибровки камеры, зависящие главным образом от угла поля изображения камеры и ее расположения относительно тестового полигона. Рисунки 2 и 3 определяют прогнозируемую точность решения задачи калибровки в зависимости от выбранных параметров.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
© Лунев А. А., 2006