After deciding on an encoding, the second
decision to make in using a genetic algorithm is how to perform selection —
that is, how to choose the individuals in the population that will create
offspring for the next generation, and how many offspring each will create. The
purpose of selection is, of course, to emphasize the fitter individuals in the
population in hopes that their offspring will in turn have even higher fitness.
Selection has to be balanced with variation from crossover and mutation (the
"exploitation/exploration balance"): too-strong selection means that suboptimal
highly fit individuals will take over the population, reducing the diversity
needed for further change and progress; too-weak selection will result in
too-slow evolution. As was the case for encodings, numerous selection schemes
have been proposed in the GA literature. Below I will describe some of the most
common methods. As was the case for encodings, these descriptions do not
provide rigorous guidelines for which method should be used for which problem;
this is still an open question for GAs. (For more technical comparisons of
different selection methods, see Goldberg and Deb 1991, Back and Hoffmeister
1991, de la Maza and Tidor 1993, and Hancock 1994.)
Fitness-Proportionate Selection with "Roulette Wheel" and
"Stochastic Universal" Sampling
Holland's original GA used
fitness-proportionate selection, in which the "expected value" of an individual
(i.e., the expected number of times an individual will be selected to
reproduce) is that individual's fitness divided by the average fitness of the
population. The most common method for implementing this is "roulette wheel"
sampling, described in chapter 1: each individual is assigned a slice of
a circular "roulette wheel," the size of the slice being proportional to the
individual's fitness. The wheel is spun N times, where N is the number of
individuals in the population. On each spin, the individual under the wheel's
marker is selected to be in the pool of parents for the next generation. This
method can be implemented as follows:
-
Sum the total expected value of individuals in the population. Call this sum T.
-
Repeat N times:
Choose a random integer r
between 0 and T.
Loop through the individuals in the
population, summing the expected values, until the sum is greater than or equal
to r. The individual whose expected value puts the sum over this limit is the
one selected.
This stochastic method statistically
results in the expected number of offspring for each individual. However, with
the relatively small populations typically used in GAs, the actual number of
offspring allocated to an individual is often far from its expected value (an
extremely unlikely series of spins of the roulette wheel could even allocate
all offspring to the worst individual in the population). James Baker (1987)
proposed a different sampling method—"stochastic universal sampling" (SUS)—to
minimize this "spread" (the range of possible actual values, given an expected
value). Rather than spin the roulette wheel N times to select N parents, SUS
spins the wheel once—but with N equally spaced pointers, which are used to
selected the N parents. Baker (1987) gives the following code fragment for SUS
(in C):
ptr = Rand(); /* Returns random number uniformly distributed in [0,1]*/
for (sum = i = 0; i < N; i + + )
for (sum += ExpVal(i,t); sum > ptr; ptr++)
Select
(i);
where i is an index over population members and where ExpVal(i,t) gives
the expected value of individual i at time t. Under this method,
each individual i is guaranteed to reproduce at least ExpVal(i,t) times
but no more than ExpVal(i,t) times. (The proof of this is left as an exercise.)
SUS does not solve the major problems with
fitness-proportionate selection. Typically, early in the search the fitness
variance in the population is high and a small number of individuals are much
fitter than the others. Under fitness-proportionate selection, they and their
descendents will multiply quickly in the population, in effect preventing the
GA from doing any further exploration. This is known as "premature
convergence." In other words, fitness-proportionate selection early on often
puts too much emphasis on "exploitation" of highly fit strings at the expense
of exploration of other regions of the search space. Later in the search, when
all individuals in the population are very similar (the fitness variance is
low), there are no real fitness differences for selection to exploit, and
evolution grinds to a near halt. Thus, the rate of evolution depends on the
variance of fitnesses in the population.
Sigma Scaling
To address such problems, GA
researchers have experimented with several "scaling" methods—methods for
mapping "raw" fitness values to expected values so as to make the GA less
susceptible to premature convergence. One example is "sigma scaling" (Forrest
1985; it was called "sigma truncation" in Goldberg 1989a), which keeps the
selection pressure (i.e., the degree to which highly fit individuals are
allowed many offspring) relatively constant over the course of the run rather
than depending on the fitness variances in the population. Under sigma scaling,
an individual's expected value is a function of its fitness, the population
mean, and the population standard deviation. A example of sigma scaling would
be
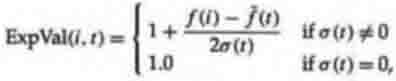
where ExpVal(i,t) is the expected value of individual i at time t, f(i) is the
fitness of i, f(t) is the mean fitness of the population at time t, and A(t) is
the standard deviation of the population fitnesses at time t. This function,
used in the work of Tanese (1989), gives an individual with fitness one
standard deviation above the mean 1.5 expected offspring. If ExpVal(i,t) was
less than 0, Tanese arbitrarily reset it to 0.1, so that individuals with very
low fitness had some small chance of reproducing.
At the beginning of a run, when the
standard deviation of fitnesses is typically high, the fitter individuals will
not be many standard deviations above the mean, and so they will not be
allocated the lion's share of offspring. Likewise, later in the run, when the
population is typically more converged and the standard deviation is typically
lower, the fitter individuals will stand out more, allowing evolution to
continue.
Elitism
"Elitism," first introduced
by Kenneth De Jong (1975), is an addition to many selection methods that forces
the GA to retain some number of the best individuals at each generation. Such
individuals can be lost if they are not selected to reproduce or if they are
destroyed by crossover or mutation. Many researchers have found that elitism
significantly improves the GA's performance.
Boltzmann Selection
Sigma scaling keeps the
selection pressure more constant over a run. But often different amounts of
selection pressure are needed at different times in a run—for example, early on
it might be good to be liberal, allowing less fit individuals to reproduce at
close to the rate of fitter individuals, and having selection occur slowly
while maintaining a lot of variation in the population. Later it might be good
to have selection be stronger in order to strongly emphasize highly fit
individuals, assuming that the early diversity with slow selection has allowed
the population to find the right part of the search space.
One approach to this is "Boltzmann
selection" (an approach similar to simulated annealing), in which a
continuously varying "temperature" controls the rate of selection according to
a preset schedule. The temperature starts out high, which means that selection
pressure is low (i.e., every individual has some reasonable probability of
reproducing). The temperature is gradually lowered, which gradually increases
the selection pressure, thereby allowing the GA to narrow in ever more closely
to the best part of the search space while maintaining the "appropriate" degree
of diversity. For examples of this approach, see Goldberg 1990, de la Maza and
Tidor 1991 and 1993, and Priigel-Bennett and Shapiro 1994. A typical
implementation is to assign to each individual i an expected value,
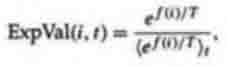
where T is temperature and <>t denotes the average over the population at time
t. Experimenting with this formula will show that, as T decreases, the
difference in ExpVal(i,t) between high and low fitnesses increases. The desire
is to have this happen gradually over the course of the search, so temperature
is gradually decreased according to a predefined schedule. De la Maza and Tidor
(1991) found that this method outperformed fitness-proportionate selection on a
small set of test problems. They also (1993) compared some theoretical
properties of the two methods.
Fitness-proportionate selection is commonly
used in GAs mainly because it was part of Holland's original proposal and
because it is used in the Schema Theorem, but, evidently, for many applications
simple fitness-proportionate selection requires several "fixes" to make it work
well. In recent years completely different approaches to selection (e.g., rank
and tournament selection) have become increasingly common.
Rank Selection
Rank selection is an
alternative method whose purpose is also to prevent too-quick convergence. In
the version proposed by Baker (1985), the individuals in the population are
ranked according to fitness, and the expected value of each individual depends
on its rank rather than on its absolute fitness. There is no need to scale
fitnesses in this case, since absolute differences in fitness are obscured.
This discarding of absolute fitness information can have advantages (using
absolute fitness can lead to convergence problems) and disadvantages (in some
cases it might be important to know that one individual is far fitter than its
nearest competitor). Ranking avoids giving the far largest share of offspring
to a small group of highly fit individuals, and thus reduces the selection
pressure when the fitness variance is high. It also keeps up selection pressure
when the fitness variance is low: the ratio of expected values of individuals
ranked i and i+1 will be the same whether their absolute fitness differences
are high or low.
The linear ranking method proposed by Baker
is as follows: Each individual in the population is ranked in increasing order
of fitness, from 1 to N. The user chooses the expected value Max of the
individual with rank N, with Max eO. The expected value of each
individual i in the population at time t is given by
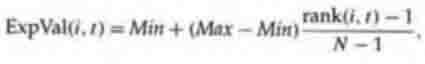 (5.1)
(5.1)
where Min is the expected value of the individual with rank 1. Given the
constraints MaxeO and iExpVal(i,t) = N (since population size stays
constant from generation to generation), it is required that 1 d Maxd 2 and Min
= 2 Max. (The derivation of these requirements is left as an exercise.)
At each generation the individuals in the
population are ranked and assigned expected values according to equation 5.1.
Baker recommended Max=1.1 and showed that this scheme compared favorably to
fitnessproportionate selection on some selected test problems. Rank selection
has a possible disadvantage: slowing down selection pressure means that the GA
will in some cases be slower in finding highly fit individuals. However, in
many cases the increased preservation of diversity that results from ranking
leads to more successful search than the quick convergence that can result from
fitness proportionate selection. A variety of other ranking schemes (such as
exponential rather than linear ranking) have also been tried. For any ranking
method, once the expected values have assigned, the SUS method can be used to
sample the population (i.e., choose parents).
As was described in chapter 2 above,
a variation of rank selection with elitism was used by Meyer and Packard for
evolving condition sets, and my colleagues and I used a similar scheme for
evolving cellular automata. In those examples the population was ranked by
fitness and the top E strings were selected to be parents. The N E ffspring
were merged with the E parents to create the next population. As was mentioned
above, this is a form of the so-called (1/4 + ») strategy used in the evolution
strategies community. This method can be useful in cases where the fitness
function is noisy (i.e., is a random variable, possibly returning different
values on different calls on the same individual); the best individuals are
retained so that they can be tested again and thus, over time, gain
increasingly reliable fitness estimates.
Tournament Selection
The fitness-proportionate
methods described above require two passes through the population at each
generation: one pass to compute the mean fitness (and, for sigma scaling, the
standard deviation) and one pass to compute the expected value of each
individual. Rank scaling requires sorting the entire population by rank—a
potentially time-consuming procedure. Tournament selection is similar to rank
selection in terms of selection pressure, but it is computationally more
efficient and more amenable to parallel implementation.
Two individuals are chosen at random from
the population. A random number r is then chosen between 0 and 1. If r < k
(where k is a parameter, for example 0.75), the fitter of the two individuals
is selected to be a parent; otherwise the less fit individual is selected. The
two are then returned to the original population and can be selected again. An
analysis of this method was presented by Goldberg and Deb (1991).
Steady-State Selection
Most GAs described in the
literature have been "generational"—at each generation the new population
consists entirely of offspring formed by parents in the previous generation
(though some of these offspring may be identical to their parents). In some
schemes, such as the elitist schemes described above, successive generations
overlap to some degree—some portion of the previous generation is retained in
the new population. The fraction of new individuals at each generation has been
called the "generation gap" (De Jong 1975). In steady-state selection, only a
few individuals are replaced in each generation: usually a small number of the
least fit individuals are replaced by offspring resulting from crossover and
mutation of the fittest individuals. Steady-state GAs are often used in
evolving rule-based systems (e.g., classifier systems; see Holland 1986) in
which incremental learning (and remembering what has already been learned) is
important and in which members of the population collectively (rather than
individually) solve the problem at hand. Steady-state selection has been
analyzed by Syswerda (1989, 1991), by Whitley (1989), and by De Jong and Sarma
(1993).
GENETIC OPERATORS
The third decision to make
in implementing a genetic algorithm is what genetic operators to use. This
decision depends greatly on the encoding strategy. Here I will discuss
crossover and mutation mostly in the context of bit-string encodings, and I
will mention a number of other operators that have been proposed in the GA
literature.
Crossover
It could be said that the
main distinguishing feature of a GA is the use of crossover. Single-point
crossover is the simplest form: a single crossover position is chosen at random
and the parts of two parents after the crossover position are exchanged to form
two offspring. The idea here is, of course, to recombine building blocks
(schemas) on different strings. Single-point crossover has some shortcomings,
though. For one thing, it cannot combine all possible schemas. For example, it
cannot in general combine instances of 11*****1 and ****ll**to form an instance
of 11**11*1. Likewise, schemas with long defining lengths are likely to be
destroyed under single-point crossover. Eshelman, Caruana, and Schaffer (1989)
call this "positional bias": the schemas that can be created or destroyed by a
crossover depend strongly on the location of the bits in the chromosome.
Single-point crossover assumes that short, low-order schemas are the functional
building blocks of strings, but one generally does not know in advance what
ordering of bits will group functionally related bits together—this was the
purpose of the inversion operator and other adaptive operators described above.
Eshelman, Caruana, and Schaffer also point out that there may not be any way to
put all functionally related bits close together on a string, since particular
bits might be crucial in more than one schema. They point out further that the
tendency of single-point crossover to keep short schemas intact can lead to the
preservation of hitchhikers—bits that are not part of a desired schema but
which, by being close on the string, hitchhike along with the beneficial schema
as it reproduces. (This was seen in the "Royal Road" experiments, described
above in chapter 4.) Many people have also noted that singlepoint crossover
treats some loci preferentially: the segments exchanged between the two parents
always contain the endpoints of the strings.
To reduce positional bias and this
"endpoint" effect, many GA practitioners use two-point crossover, in which two
positions are chosen at random and the segments between them are exchanged.
Two-point crossover is less likely to disrupt schemas with large defining
lengths and can combine more schemas than single-point crossover. In addition,
the segments that are exchanged do not necessarily contain the endpoints of the
strings. Again, there are schemas that two-point crossover cannot combine. GA
practitioners have experimented with different numbers of crossover points (in
one method, the number of crossover points for each pair of parents is chosen
from a Poisson distribution whose mean is a function of the length of the
chromosome). Some practitioners (e.g., Spears and De Jong (1991)) believe
strongly in the superiority of "parameterized uniform crossover," in which an
exchange happens at each bit position with probability p (typically 0.5
d p d 0.8). Parameterized uniform crossover has no positional bias—any
schemas contained at different positions in the parents can potentially be
recombined in the offspring. However, this lack of positional bias can prevent
coadapted alleles from ever forming in the population, since parameterized
uniform crossover can be highly disruptive of any schema.
Given these (and the many other variants of
crossover found in the GA literature), which one should you use? There is no
simple answer; the success or failure of a particular crossover operator
depends in complicated ways on the particular fitness function, encoding, and
other details of the GA. It is still a very important open problem to fully
understand these interactions. There are many papers in the GA literature
quantifying aspects of various crossover operators (positional bias, disruption
potential, ability to create different schemas in one step, and so on), but
these do not give definitive guidance on when to use which type of crossover.
There are also many papers in which the usefulness of different types of
crossover is empirically compared, but all these studies rely on particular
small suites of test functions, and different studies produce conflicting
results. Again, it is hard to glean general conclusions. It is common in recent
GA applications to use either two-point crossover or parameterized uniform
crossover with p H 0.7-0.8.
For the most part, the comments and
references above deal with crossover in the context of bit-string encodings,
though some of them apply to other types of encodings as well. Some types of
encodings require specially defined crossover and mutation operators—for
example, the tree encoding used in genetic programming, or encodings for
problems like the Traveling Salesman problem (in which the task is to find a
correct ordering for a collection of objects).
Most of the comments above also assume that
crossover's ability to recombine highly fit schemas is the reason it should be
useful. Given some of the challenges we have seen to the relevance of schemas
as a analysis tool for understanding GAs, one might ask if we should not
consider the possibility that crossover is actually useful for some entirely
different reason (e.g., it is in essence a "macro-mutation" operator that
simply allows for large jumps in the search space). I must leave this question
as an open area of GA research for interested readers to explore. (Terry Jones
(1995) has performed some interesting, though preliminary, experiments
attempting to tease out the different possible roles of crossover in GAs.) Its
answer might also shed light on the question of why recombination is useful for
real organisms (if indeed it is)—a controversial and still open question in
evolutionary biology.
Mutation
A common view in the GA
community, dating back to Holland's book Adaptation in Natural and ARtificial
Systems, is that crossover is the major instrument of variation and innovation
in GAs, with mutation insuring the population against permanent fixation at any
particular locus and thus playing more of a background role. This differs from
the traditional positions of other evolutionary computation methods, such as
evolutionary programming and early versions of evolution strategies, in which
random mutation is the only source of variation. (Later versions of evolution
strategies have included a form of crossover.)
However, the appreciation of the role of
mutation is growing as the GA community attempts to understand how GAs solve
complex problems. Some comparative studies have been performed on the power of
mutation versus crossover; for example, Spears (1993) formally verified the
intuitive idea that, while mutation and crossover have the same ability for
"disruption" of existing schemas, crossover is a more robust "constructor" of
new schemas. Muhlenbein (1992, p. 15), on the other hand, argues that in many
cases a hill-climbing strategy will work better than a GA with crossover and
that "the power of mutation has been underestimated in traditional genetic
algorithms." As we saw in the Royal Road experiments in chapter 4. it is
not a choice between crossover or mutation but rather the balance among
crossover, mutation, and selection that is all important. The correct balance
also depends on details of the fitness function and the encoding. Furthermore,
crossover and mutation vary in relative usefulness over the course of a run.
Precisely how all this happens still needs to be elucidated. In my opinion, the
most promising prospect for producing the right balances over the course of a
run is to find ways for the GA to adapt its own mutation and crossover rates
during a search. Some attempts at this will be described below.
Other Operators and Mating Strategies
Though most GA applications
use only crossover and mutation, many other operators and strategies for
applying them have been explored in the GA literature. These include inversion
and gene doubling (discussed above) and several operators for preserving
diversity in the population. For example, De Jong (1975) experimented with a
"crowding" operator in which a newly formed offspring replaced the existing
individual most similar to itself. This prevented too many similar individuals
("crowds") from being in the population at the same time. Goldberg and
Richardson (1987) accomplished a similar result using an explicit "fitness
sharing" function: each individual's fitness was decreased by the presence of
other population members, where the amount of decrease due to each other
population member was an explicit increasing function of the similarity between
the two individuals. Thus, individuals that were similar to many other
individuals were punished, and individuals that were different were rewarded.
Goldberg and Richardson showed that in some cases this could induce appropriate
"speciation," allowing the population members to converge on several peaks in
the fitness landscape rather than all converging to the same peak. Smith,
Forrest, and Perelson (1993) showed that a similar effect could be obtained
without the presence of an explicit sharing function.
A different way to promote diversity is to
put restrictions on mating. For example, if only sufficiently similar
individuals are allowed to mate, distinct "species" (mating groups) will tend
to form. This approach has been studied by Deb and Goldberg (1989). Eshelman
(1991) and Eshelman and Schaffer (1991) used the opposite tack: they disallowed
matings between sufficiently similar individuals ("incest"). Their desire was
not to form species but rather to keep the entire population as diverse as
possible. Holland (1975) and Booker (1985) have suggested using "mating
tags"—parts of the chromosome that identify prospective mates to one another.
Only those individuals with matching tags are allowed to mate (a kind of
"sexual selection" procedure). These tags would, in principle, evolve along
with the rest of the chromosome to adaptively implement appropriate
restrictions on mating. Finally, there have been some experiments with
spatially restricted mating (see, e.g., Hillis 1992): the population evolves on
a spatial lattice, and individuals are likely to mate only with individuals in
their spatial neighborhoods. Hillis found that such a scheme helped preserve
diversity by maintaining spatially isolated species, with innovations largely
occurring at the boundaries between species.
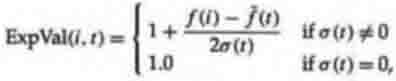
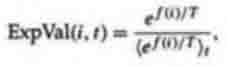
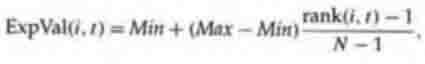 (5.1)
(5.1)