Автореферат
Постановка задачі
Зварювання - технологічний процес, широко застосовуваний у всіх галузях для виготовлення нових і
ремонту експлуатованих механізмів, конструкцій й устаткування.
В останні роки швидко розвивається автоматизації дугового зварювання (зварювання плавленням) із застосуванням
промислових роботів, що може застосовуватися у всіх галузях при виготовленні металоконструкцій. Зварюванням
плавленням можна з'єднувати практично всі використовувані для виготовлення конструкцій метали й сплави будь-якої
товщини. Цей процес дуже шкідливий для людини, пов'язаний із сильним шумом, більшими температурами, впливом
диму й інтенсивного світла (іскріння), автоматизація забезпечує високу якість швів, більшу стабільність і
швидкість роботи.
Роботи, застосовувані для автоматизації дугового зварювання, являють собою універсальні перепрограмувальні
маніпулятори. Система керування зварювальним роботом повинна забезпечувати швидке настроювання параметрів
керування для заданої траєкторії руху зварювального пальника, що може бути задана аналітично функцією переміщення
пальника в часі або задане оператором безліччю крапок, які можуть бути отримані експериментально. Під час
зварювання оператор повинен мати можливість подкоректувати траєкторію, щоб забезпечити точність позиціювання
не більше необхідної - ±0.1мм. Також необхідно враховувати типи матеріалів виробів, що зварюють, і їхню товщину,
від яких буде залежати швидкість переміщення голівки зварювального пальника. Якщо швидкість пальника буде
відрізнятися від заданої, то не буде забезпечена висока якість швів, навіть при нульовій помилці позиціювання.
Так як менша швидкість досить не розплавить краї матеріалів, що зварюють, а більша - навпаки переплавить їх.
Основною проблемою керування дуговим зварюванням є проблема точного позиціювання, тобто точного відстеження заданої
траєкторії в просторі й у часі, при безперервному контурному керуванні для виконання щодо складних маніпуляційних
завдань. Основними факторами, що породжують цю проблему, є істотна нелінійність динамічної й кінематичної моделі,
динамічна взаємозв'язок між окремими системами, а також незаплановані фактори: зміна програми траєкторії або
несподівана зміна корисного навантаження.
Більшість раніше застосовуваних методів керування або не враховували зміну динаміки в часі, або були настільки
складні й громіздкі в обчислювальному відношенні, що вимагали дуже великої кількості обчислень на кожному кроці
за короткий проміжок часу. У першому випадку не забезпечувалися задані вимоги до динамічного регулювання, а в
другому - приводило до необхідності використання дуже потужних і дорогих контролерів.
Для усунення проблем нелінійності диференціальних рівнянь застосовується лінеаризація динамічної моделі. Лінеаризація
за допомогою класичних методів з використанням розкладання нелінійних диференціальних рівнянь у ряд Тейлора в околиці
робочої крапки має потребу в перенастроюванні параметрів керування при зміні робочої крапки.
Для усунення цих же проблем можна застосувати новий загальний метод компенсації взаємозв'язків і нелінейностей диференціальних
рівнянь динаміки з використанням дифеоморфного перетворення й теорії Чи алгебри. Даний підхід заснований на ідеї одержання
"зовнішньої лінеаризації" складної нелінійної системи з використанням дифеоморфного перетворення координат і нелінійний
обратний зв'язку по стану. Цей метод дозволяє забезпечити поблочну розв'язку виходу; конструктивний алгоритм знаходження
нелінійного зворотного зв'язку для підсистем, у яких число виходів може бути менше або дорівнює числу входів; розв'язку
виходів нелінійним зворотним зв'язком з погляду стану системи; для забезпечення стійкості системи керування нелінійний
зворотний зв'язок з'єднується з контролером оптимальної корекції помилок.
Перевагою цього методу є те, що параметри керування не мають потреби в пері настроюванню, оскільки лінеаризація проводиться
не в конкретній крапці, а на цілій підмножині нелінійних площин.
Угору
1. АНАЛІЗ ІСНУЮЧИХ АЛГОРИТМІВ УПРАВЛІННЯ МАНІПУЛЯЦІЙНИМИ ПРОМИСЛОВИМИ РОБОТАМИ.
1.1. Аналіз існуючих методів синтезу алгоритмів керування маніпуляционним промисловим роботом.
Планування траєкторії руху маніпулятора промислового робота здійснюється за допомогою алгоритмів керування плануванням.
Ці алгоритми керування розглядаються як нелінійні алгоритми поділу командного руху по ступенях рухливості маніпулятора.
Їхня реалізація пов'язана з рішенням нелінійних рівнянь, що характеризують конфігурацію механізму при заданому положенні
робочих органів промислових роботів. Для рішення таких нелінійних завдань прибігають або до допомоги ЕОМ, або імітаціонному
моделюванню з використанням реальних моделей маніпуляционних систем.
Для лінеаризації рівнянь, що описують поводження маніпуляціоннї системи при малих змінах координат елементів механізму,
звичайно прибігають до диференціювання за часом координат положення ланок у складному механізмі, зв'язаному нелінійними
залежностями або до компенсації нелінійностей і взаємодії за допомогою регуляторів і зворотного зв'язку.
Завданням керування є вироблення алгоритму необхідного функціонування приводів маніпулятора. При цьому використається
кілька методів керування плануванням траєкторії руху маніпулятора промислового робота.
Метод керування по векторі швидкості складається в завданні швидкості руху робочих органів маніпуляціой системи
у вигляді шестимерного вектора, що представляє проекції векторів кутової швидкості робітника органа й швидкості його
деякої крапки в якій-небудь системі координат, які передбачаються алгоритмами керування таким чином, щоб повністю
визначити швидкість робочого органа в поточній крапці траєкторії.
Безпосереднє використання цього рішення для цілей керування обмежуються виникненням у процесі керування вирождених
конфігурацій механізму, які повинні враховуватися алгоритмом керування. Такий метод керування є ефективним при
необхідності швидкого перекладу робочого органа з одного положення в інше, не потребуючій високій точності позиціювання.
Крім того, метод має достатню складність реалізації.
Метод послідовних коректувань положення найбільше широко застосовується в цифрових системах керування. У цьому
випадку алгоритм керування по векторі швидкості формується як збільшення координат маніпулятора за один цикл обчислення
алгоритму.
Недоліком методу є часта вибірка вузлових крапок складної траєкторії, щоб переходи від однієї крапки до іншої
при плануванні траєкторії руху не міняли принципово необхідної картини руху.
Наближені методи. При синтезі системи керування маніпулятором користуються наближеними рішеннями, які випливають із
обмеженості завдання значень координат. Звичайно беруть по трьох значення: два крайніх й одне середнє, і для них обчислюють
зворотну матрицю Якобі, що залежить від конфігурації маніпулятора, для всіх інших значень координат (у тому числі й вузлових,
характерних крапок траєкторії) зворотна матриця обчислюється інтерполяцією. У багатьох випадках, особливо при наявності
зворотного зв'язку по положенню, цього виявляється цілком достатньо при досягненні кінцевої мети керування.
Недоліком методу є виникаючі при інтерполяції помилки, що досягають великого значення, особливо при відсутності зворотного
зв'язку по положенню.
Метод керування по векторі сили. До недоліків методу керування по векторі швидкості варто віднести неможливість
забезпечувати формалізацію прагнення переміщення робочих органів промислових роботів у заданому напрямку, якщо на заданій
траєкторії зустрічаються крапки, у яких матриця конфігурації маніпулятора є вирожденой.
Тенденція до спрощення процесу керування й обумовлених цим обчислень привели до використання методу керування по векторі сили,
у якому імітаційно реалізується ідея керування по заданому напрямку. У дійсності до маніпулятора не додаються ніякі сили, але
приводи, що стежать, розвивають таку сукупність узагальнених сил, які динамічно еквівалентні заданим силам, що імітують їхній
додаток до маніпулятора. Обчислювач, одержавши на вході сигнали, що задають, визначає узагальнені сили, віднесені до координат,
безпосередньо керованим приводом. У свою чергу, приводи постійно виробляють такі узагальнені сили, які виходять на виході
обчислювача. У ці узагальнені сили можуть автоматично вводитися виправлення регуляторами й компенсаторами.
1.2. Аналіз існуючих методів компенсації нелінейностей і розв'язки взаємодій у маніпуляційних промислових роботах.
Основним завданням керування промисловими роботами є генерування зовнішніх моментів u(t) таким чином, щоб рух робота
здійснювалося по обраній траєкторії. Рух робота звичайно здійснюється двома різними контрольованими фазами. Першої з них
є контрольна фаза грубого руху, під час якої робот переміщається від споконвічної позиції в околицю місця розташування
заданої мети уздовж попередньо певної траєкторії. Другою контрольною фазою є стадія точного руху, коли робочий орган робота
динамічно взаимодіє з об'єктом, використовуючи при цьому інформаційний канал зворотного зв'язку від зовнішніх датчиків для
виконання завдання.
У випадку, якщо в роботах використається традиційна техніка, що стежить, то нелінійності й взаємодії, що є присутнім у динаміку
маніпулятора, не можуть бути скомпенсовані на стадії грубого руху. З підвищенням вимог до робочих характеристик промислових
роботів стає необхідним прийняття в увагу перерахованих динамічних ефектів. По цьому протягом останнього часу була запропонована
велика кількість удосконалень у схемах й алгоритмах безпосереднього контролю промислових роботів.
Деякими дослідниками було запропоновано використати лінеаризовані моделі систем як основу для подальшої реалізації розв'язки
регулювання. Кан і Рот розробили наближену модель оптимального контролера, що приводила до субоптимального регулювання.
Субоптимальне регулювання виникало в результаті наближеної заміни нелінійної системи лінійної й наступного аналітичного
знаходження оптимального керування для лінійної системи. Був також запропонований метод лінійного регулювання по багатьом
змінним. Однак, заснована на лінеаризованій моделі система регулювання може виявитися практично неприйнятної, якщо реальні
робочі умови почнуть відрізнятися від умов, закладених при лінеаризації. Це може привести до небажаних відхилень реакції робота
від заданої траєкторії, як це було показано Фрюндом при моделюванні різних методів регулювання.
Одним з перших методів, у яких робот розглядається як нелінійна, взаємозалежна система з багатьма входами й багатьма виходами,
була методика обчислень обертаючих моментів, досліджена Підлогою, Маркевичем. Цей метод заснований на використанні негативних
зворотних і позитивної зворотних зв'язків. Позитивний зворотний зв'язок використається для компенсації сил взаємодії, що виникають
між зчленуваннями, а за допомогою негативного зворотного зв'язку виробляється обчислення необхідних коригувальних обертальних
моментів для компенсації будь-яких відхилень від заданої траєкторії. При цьому покладається , що можливо точне обчислення
інерційних сил реакції, сили Кориолиса й доцентрової сили, а також гравітаційних сил. Таким чином, експлуатаційні характеристики
даної системи регулювання в значній мірі залежать від точності використовуваної моделі. Метод визначення обертаючих моментів
вимагає значної кількості обчислень, що часто розглядається як його недолік.
Регулювання швидкості спроектованого руху являє собою методику визначення змінних швидкостей руху зчленування, необхідних для
забезпечення переміщення кінцевої крапки робота в заданому напрямку. При такій схемі керування всі встановлені траєкторії
задаються в декартових координатах. Це є певною перевагою, оскільки більшість користувачів, імовірно, з більшою легкістю можуть
задати послідовність переміщення в декартових координатах, чим у змінних координатах місця розташування з'єднання. Способи
обчислення обертаючих моментів і регулювання швидкості спроектованого руху сполучені в методі регулювання прискорення
спроектованого руху. У ЦЬОМУ методі передбачається, що необхідні місця розташування, швидкості й прискорення заданого руху руки
визначаються користувачем. Перераховані методи також мають недоліки: вони вимагають наявності деталізованої динамічної моделі й
тривалого машинного часу для здійснення обчислень.
Основне достоїнство різних методів адаптивного регулювання є відсутність необхідності використання моделі динаміки робота.
В еталонній моделі адаптивного контролю вибирається відповідним еталоном модель, а алгоритм адаптації модифікує коефіцієнти
підсилення в каналах зворотного зв'язку контролерів. Алгоритм адаптації задається різницею між вихідними сигналами еталонної
моделі й фактичних вихідних периметрів робота. Керування роботом здійснюється регулюванням коефіцієнтів підсилення в каналах
зворотного зв'язку для місця розташування й швидкості, так щоб його характеристики замкнутого контуру минулого близькі до
еталонної моделі. Недоліком методу є копіткість і багатомірність при реалізації.
Новий плин у проектуванні керуючих систем для промислових роботів є використання теорії систем зі змінною структурою. У системах
зі змінною структурою на поверхні перемикання має місце так званий ковзний режим. При роботі в ковзному режимі система залишається
нечутливої до змін параметрів і збурюванням. Створення керування, індуцирований ковзний режим, не вимагає точного моделювання;
виявляється достатнім тільки знати співвідношення між параметрами моделі. Однак, цей метод володіє одним недоліком, що випливає
з мінімізації часу рішення: точне визначення моментів включення регулюючих вхідних сигналів виявляється скрутним.
Угору
2. МАТЕМАТИЧНА МОДЕЛЬ ПРОМИСЛОВОГО РОБОТА ТИПУ PUMA-560 З МІНІМАЛЬНОЮ КОНФІГУРАЦІЄЮ
2.1. Математична модель кінематики промислового робота
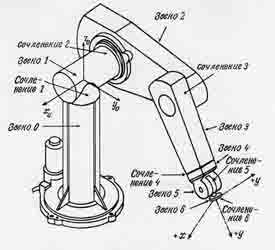 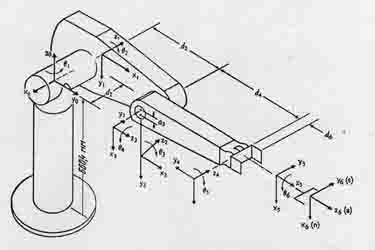
Рис. 2.1 - Манипулятор PUMA-560.
Поняття "робот з мінімальною конфігурацією" означає, що будуть розглядатися три перші ланки роботів, які визначають положення
схвата маніпулятора в просторі. Інакше кажучи, не будуть розглядатися останні три щаблі рухливості, які визначають орієнтацію
схвата.
Для розглянутого робота згідно відомі матриці однорідних перетворень координат для переходу від i-ої до (i-1)-ой системи координат:
Для маніпуляційного робота типу PUMA-560, всі зчленування якого обертальні, параметри di и
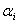 є конструктивними параметрами зчленувань. Параметр qi
є змінною величиною. Конкретні значення конструктивних параметрів, наведені в таблицях 1 й 2. є конструктивними параметрами зчленувань. Параметр qi
є змінною величиною. Конкретні значення конструктивних параметрів, наведені в таблицях 1 й 2.
Таблиця 1
Конструктивні параметри робота PUMA-560
| a2,м |
a3,м |
a4,м |
a5,м |
| 0.432 |
0.019 |
0.125 |
0.432 |
Таблиця 2
Масо-інерційні характеристики робота PUMA-560
| Ланка |
Маса |
Центры мас |
Радіуси инерції |
| i |
mi,кг |
xi,м |
yi,м |
zi,м |
kxi,м |
kyi,м |
kzi,м |
| 1 |
33.5 |
0 |
0 |
0.08 |
0.0451 |
0.0451 |
0.00579 |
| 2 |
73.3 |
-0.216 |
0 |
0.2175 |
0.05657 |
0.1847 |
0.1408 |
| 3 |
36.3 |
0 |
0 |
0.216 |
0.06728 |
0.06791 |
0.0036 |
| 4 |
8.95 |
0 |
0.02 |
0 |
0.00316 |
0.00211 |
0.00316 |
Для одержання однорідної матриці 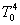 , що визначає положення схвата маніпулятора
в просторі, необхідно виконати (відповідно до формалізму Денавита-Хартенберга) операції перемножування матриць , що визначає положення схвата маніпулятора
в просторі, необхідно виконати (відповідно до формалізму Денавита-Хартенберга) операції перемножування матриць
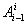 для i=1 для i=1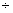 4: 4:
|
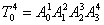
|
(2.5) |
У даній матриці нас цікавить 4-й стовпець, що є вектором положення схвата розглянутого маніпулятора, координати якого мають вигляд:
де
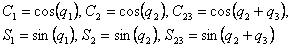
Отриманий вектор 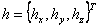 є нелінійним відображенням вихідних координат системи,
що надалі використається при лінеаризації рівнянь динаміки маніпулятора. є нелінійним відображенням вихідних координат системи,
що надалі використається при лінеаризації рівнянь динаміки маніпулятора.
2. Математична модель динаміки промислового робота типу PUMA-560 у формі рівняння Лагранжа-Эйлера
Розглянемо робот з n кінематичними парами, що не має надлишкових ступенів рухливості, у якого n - мірний вектор моментів
t(t) у кінематичних парах пов'язаний з n - мірним вектором Q(t) кутів повороту в шарнірах нелінійним динамічним рівнянням руху:
|
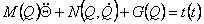
|
(2.9) |
де M(Q) - симетрична позитивно певна матриця інерції розмірністю n х n,
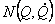 - n - мірний вектор-стовпець моментів, обумовлених силами Кориолиса й відцентровими силами: - n - мірний вектор-стовпець моментів, обумовлених силами Кориолиса й відцентровими силами:
|
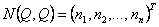
|
(2.10) |
|
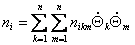
|
(2.11) |
G(Q) - n - мірний вектор гравітаційного навантаження;
Рівняння (2.9) описує динаміку маніпулятора у формі Эйлера-Лагранжа. Для приведення нелінійних диференціальних рівнянь (2.9)
до спеціального виду, уведемо позначення:
|
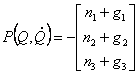
|
(2.12) |
Тоді рівняння (2.9) прийме вид:
|
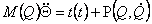
|
(2.13) |
Рівняння (2.13) надалі буде використано при одержанні нелінійного рівняння спеціального виду.
Завдання керування маніпулятором полягає в створенні такої системи керування, що забезпечує відстеження вектором кутів повороту
в шарнірах Q(t) будь-який заданої (опорної) траєкторії Qr(t), де Qr(t) - n - мірний вектор-стовпець
довільних функцій часу. Доцільно допустити, що ці функції мають похідні першого й другого порядків, тобто необхідні кутова швидкість
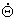 r(t) і кутове прискорення r(t) і кутове прискорення 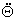 r(t)
існують і доступні безпосередньо, без необхідності операції диференціювання Qr(t). Бажано також, щоб система керування
маніпулятором забезпечувала відстеження траєкторії незалежно від маси вантажу m, тобто щоб динамічні характеристики маніпулятора
були нечутливі до величини корисного навантаження. r(t)
існують і доступні безпосередньо, без необхідності операції диференціювання Qr(t). Бажано також, щоб система керування
маніпулятором забезпечувала відстеження траєкторії незалежно від маси вантажу m, тобто щоб динамічні характеристики маніпулятора
були нечутливі до величини корисного навантаження.
Угору
3. ЛІНЕАРИЗАЦІЯ МАТЕМАТИЧНОЇ МОДЕЛІ ДИНАМІКИ ПРОМИСЛОВОГО РОБОТА ТИПУ PUMA-560
3.1 Лінеаризація математичної моделі динаміки робота на основах розкладання навряд Тейлора
Апроксимуємо нелінійну математичну модель динамічної системи (2.8) на тимчасовому інтервалі ti<t<ti+Dt
шляхом розкладання в ряд Тейлора в околиці номінальній операційної (робочої) крапки лінійної інваріантної за часом багатомірною
моделлю
|
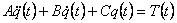
|
(3.1) |
де q(t) и T(t) - відхилення векторів кутів повороту й моментів у шарнірах від своїх номінальних значень
t(ti) і Q(ti) у робочій точці P={t(ti),Q(ti),Q(ti)}, тобто
|
q(t)=Q(t)-Q(ti)
|
(3.2) |
|
T(t)=t(t)-t(ti)
|
(3.3) |
Три матриці А, В, З розмірністю n х n, що входять у лінеаризовану модель (3.1), залежать від положення робочої крапки Р
и можуть бути, отримані з виражень:
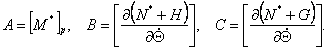
і матриця А завжди симетрична, позитивно певна й, отже, не вирождена. Рівняння (3.1) являє собою систему зв'язаних лінійних,
що не залежать від часу диференціальних рівнянь, що описують динаміку робота в збільшеннях при наявності збурювань в околиці
номінальної операційної крапки Р.
Можливі два варіанти подання лінеаризованой моделі робота (3.1), а саме: модель у просторі стану, тобто в тимчасовій області,
і модель в області комплексної змінної, тобто в частотній області.
Для складання моделі робота в просторі станів визначають елементи виражень 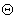 і
і 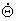 змінні стани системи, і рівняння (3.1) переписують у стандартному форматі: змінні стани системи, і рівняння (3.1) переписують у стандартному форматі:
|
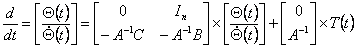
|
(3.5) |
Порядок цієї моделі дорівнює 2n, вектор стану 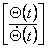 має розмірність
2n має розмірність
2n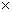 1, всі вектори розглядаються в тимчасовій області. 1, всі вектори розглядаються в тимчасовій області.
Модель робота в частотній області становимо за допомогою перетворення Лапласа з рівнянь (3.1), у результаті чого одержуємо:
|
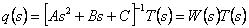
|
(3.6) |
де T(s) и q(s) - n - мірні вектори входу й виходу системи в частотній області.
3.2 Приведення рівнянь динаміки промислового робота типу PUMA-560 у формі Лагранжа-Эйлера до спеціального виду
Для одержань нелінійного диференціального рівняння спеціального виду введемо наступні позначення для узагальнених координат:
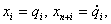
вектор (x1,x2,…,x2n) позначається X, вектор (x1,x2,…,xn)
позначається 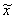 . Рівняння (2.9) можна представити в стандартній формі спеціального
виду, якщо врахувати раніше уведені позначення: . Рівняння (2.9) можна представити в стандартній формі спеціального
виду, якщо врахувати раніше уведені позначення:
|
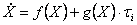
|
(3.7) |
Зміст нелінійних функцій f(x) і g(x) у рівнянні (3.7) стане зрозумілим при його записі у формі компонентів:
|

|
(3.8) |
У такий спосіб отримане векторно-матричне рівняння (3.8), на основі якого буде здійснена лінеаризація динамічної моделі
маніпулятора із застосуванням дифеоморфного перетворення координат і нелінійного зворотнього зв'язку за станом.
3.3 Лінеаризація математичної моделі динаміки робота на основі дифеоморфного перетворення координат і нелінійного
зворотнього зв'язку за станом
Для лінеаризації динамічної моделі промислового робота типу PUMA-560 уводиться нелінійний зворотний зв'язок виду:
і дифеоморфне перетворення Т(х) таке, що після здійснення нелінійного зворотного зв'язку й дифеоморфного перетворення
координат нова (перетворена) система є лінійною в Бруновской канонічній формі з розв'язаним виходом.
У вираженні (3.9) фігурують наступні позначення:
U(x) - вектор керуючих впливів, прикладених до маніпулятора робота;
а(х) - векторна функція;
b(х) - неособлива матриця;
V- вектор вхідних впливів системи;
Нелінійний зворотний зв'язок може бути представлена в наступному виді:
|
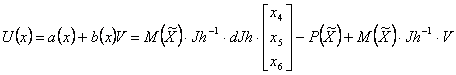
|
(3.10) |
де
|
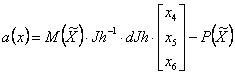
|
(3.11) |
|
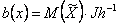
|
(3.12) |
Jh - матриця Якоби функції;
Jh-1 - матриця, зворотна матриці Якоби;
DJh - матриця, обумовлена відповідно до виражень:
|

|
(3.13) |
|

|
(3.14) |
Дифеоморфне перетворення координат має такий вигляд:
|

|
(3.15) |
де Lf- похідні Ли;
|
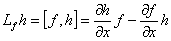
|
(3.16) |
Частні похідні 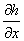 і і 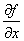 є матрицями Якоби;
є матрицями Якоби;
З використанням наведеної вище нелінійного зворотного зв'язку по стані й дифеоморфного перетворення динамічна модель
маніпулятора представляється в канонічній формі Brunovsky з декомпозицією по вихідним змінним:
|
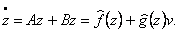
|
(3.17) |
|
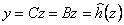
|
(3.18) |
де z - вектор стану в перетвореній системі координат розмірності (6x1);
А - блочно-діагональна матриця розмірності (6x6), що характеризує декомпозицію станів ланок перетвореної моделі робота;
В - блочно - діагональна матриця розмірності (6x3), що відбиває декомпозицію керуючих впливів на ланки перетвореної моделі робота;
С - блочно - діагональна матриця розмірності (3x6), що визначає декомпозицію вихідних координат шарнірів перетвореної моделі робота;
|
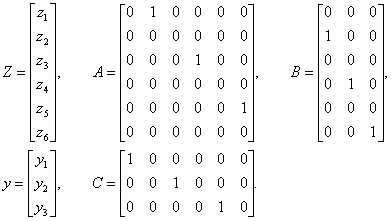
|
(3.19) |
Динамічна система, описана рівняннями (3.17) і (3.18), складається із трьох незалежних підсистем наступної форми:
|
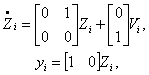
|
(3.20) |
де
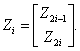
Дана лінійна система з розв'язаним виходом показаний схематично як блок BCLS (Бруновска канонічна лінійна система) на мал.3.1.
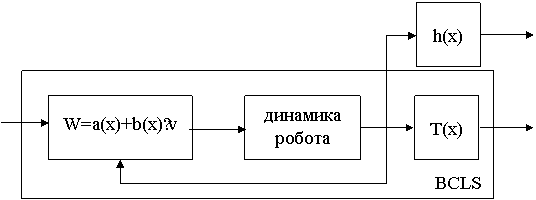
Рис.3.1 - Бруновска канонічна лінійна система
Лінеаризація, здійснювана нелінійним зворотним зв'язком, є "зовнішньою лінеаризацією" на відміну від звичайної "внутрішньої
лінеаризації" (розкладання в ряд Тейлора). Нелінійний характер вихідної системи не міняється. Лінеаризацію системи нелінійним
зворотним зв'язком можна назвати "точною лінеаризацією" у змісті керування. Точна загальна лінеаризація системи й розв'язка
виходу, здійснені нелінійним зворотним зв'язком по стані й дифеоморфним перетворенням координат, створюють лінійну систему.
Отримана система є нестійкої, тому що кожна лінійна підсистема має кратні нульові полюси. Отже, необхідно провести стабілізацію
отриманої лінійної системи.
У результаті проведеної лінеаризації динамічної моделі робота за допомогою нелінійного зворотного зв'язку по стані й дифеоморфного
перетворення координат, отримана лінеаризованна математична модель із декомпозицією стану по зчленуваннях і з розв'язаним виходом
маніпулятора. На основі отриманої математичної моделі можна синтезувати алгоритми оптимального керування маніпулятором робота добре
розробленими лінійними методами.
Угору
4. СИНТЕЗ АЛГОРИТМІВ КЕРУВАННЯ ПРОМИСЛОВИМ РОБОТОМ ТИПУ PUMA-560 МІНІМАЛЬНОЇ КОНФІГУРАЦІЇ
4.1. Синтез алгоритмів багатомірної системи керування промисловим роботом - багатомірного регулятора з комбінованим керуванням
Підхід до синтезу системи керування рухом у кінематичних парах, використовуваний у дійсній роботі, заснований на концепції так
званих "зворотних систем". Розглянемо лінійну, що не залежить від часу, багатомірну установку (об'єкт регулювання)
де u и у - m-мірні вектори - стовпці входу й виходу, a W(s) - її передатна функція у вигляді матриці розмірністю nхn.
Зворотним відображенням (інверсією) цієї установки є динамічна система, у якої передатна функція
Коли при послідовному з'єднанні об'єкту керування (4.1) передує його інверсія (4.2), на вхід якої подається необхідний
вихідний сигнал yd (t) об'єкта, інверсний регулятор буде генерувати відповідний керуючий вплив, забезпечуючи на виході
установки відтворення сигналу в (t), тому що по визначенню добуток передатної функції об'єкта і її інверсії є одинична
матриця розмірності mхm
Дана концепція може бути використана для керування нелінійними об'єктами, зокрема, стосовно до роботів. У випадку невеликих
відхилень параметрів об'єкта в околиці робочої крапки Р нелінійна установка апроксимируєтбся квазілійной інваріантної за часом
моделлю W1(s) на малом временном интервале
ti<t<ti+ t. У цьому інтервалі часу інверсія
Qi(s) установки використається як регулятор прямого каналу керування для генерування керуючого впливу uпк(t).
Потім коефіцієнти підсилення регулятора прямого каналу керування "обновляються" (настроюються) таким чином, щоб компенсувати зміни
в часі коефіцієнтів лінеаризованой моделі
Wi(s), обумовлені змінами положення робочої крапки Р. Коли регулятор прямого каналу керування є точною інверсією
об'єкта керування, помилка відстеження e(t)=yd(t)-y(t), що представляє собою різниця між входом регулятора (у) і
виходом системи (yd) будет равна нулю. Следовательно, буде дорівнює нулю. Отже, представляється логічним розглядати
помилку відстеження е(t) як міру відхилення регулятора прямого каналу керування від точної інверсії об'єкта. Ця інформація
використається для настроювання параметрів регулятора прямого каналу керування, причому настроювання ведеться таким чином, щоб
поводження регулятора були точною інверсією поводження об'єкта керування, що забезпечує якісне відстеження заданої траєкторії
yd(t). t. У цьому інтервалі часу інверсія
Qi(s) установки використається як регулятор прямого каналу керування для генерування керуючого впливу uпк(t).
Потім коефіцієнти підсилення регулятора прямого каналу керування "обновляються" (настроюються) таким чином, щоб компенсувати зміни
в часі коефіцієнтів лінеаризованой моделі
Wi(s), обумовлені змінами положення робочої крапки Р. Коли регулятор прямого каналу керування є точною інверсією
об'єкта керування, помилка відстеження e(t)=yd(t)-y(t), що представляє собою різниця між входом регулятора (у) і
виходом системи (yd) будет равна нулю. Следовательно, буде дорівнює нулю. Отже, представляється логічним розглядати
помилку відстеження е(t) як міру відхилення регулятора прямого каналу керування від точної інверсії об'єкта. Ця інформація
використається для настроювання параметрів регулятора прямого каналу керування, причому настроювання ведеться таким чином, щоб
поводження регулятора були точною інверсією поводження об'єкта керування, що забезпечує якісне відстеження заданої траєкторії
yd(t).
Окрім того, для підвищення стійкості замкнутої системи керування й поліпшення якості перехідних процесів використається регулятор
ланцюга зворотного зв'язку Ki(s), що генерує для об'єкта керування керуючий сигнал Uoc(t) у робочій крапці Р.
Коефіцієнти ланцюга зворотного зв'язку також постійно настроюються відповідно до помилки е(t) для компенсації змін
Wi(s). Крім того, при реалізації закону керування синтезується й використається додатковий сигнал
uрт(t), що відповідає робочій крапці Р. Цей сигнал допомагає поліпшити якість керування, забезпечуючи більше
швидку адаптацію до змін параметрів установки, і збільшує гнучкість системи керування. Виходячи із усього вищесказаного, загальний
закон керування визначається вираженням:
|
u(t)=uпк(t)+uос(t)+uрт(t)
|
(4.4) |
Описана методика синтезу проілюстрована блок-схемою на мал. 4.1
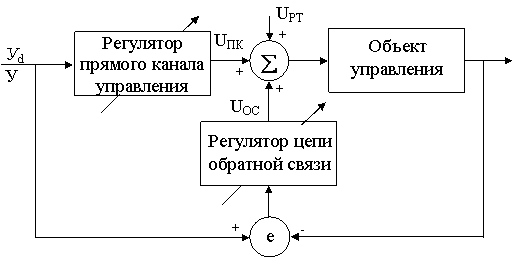
Рис. 4.1. - Структура системи управління
4.1.1. Синтез регулятора прямого каналу управління
Лінеаризовану модель (5.4.3.1) динаміки маніпулятора можна представити моделлю в частотній області (через передатну функцію)
|
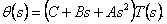
|
(4.5) |
З огляду на вищевикладене, як передатна функція Q(s) розмірністю n х n регулятора прямого каналу керування вибирається інверсія
лінеаризованой моделі (4.5), тобто
|
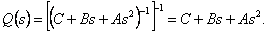
|
(4.6) |
Рівняння (4.6) дає просте вираження інверсії лінеаризованой моделі (3.1) маніпулятора, що забезпечує можливість практичної
реалізації Q(s). Необхідно відзначити, що інверсія Q(s) багатомірного об'єкта регулювання W(s) у загальному
випадку являє собою складну динамічну систему. Тоді закон керування, реалізований регулятором прямого каналу керування, задається
вираженням:
|
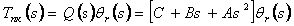
|
(4.7) |
або
|
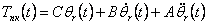
|
(4.8) |
де 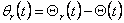 - необхідний n-мірний вектор-стовпець збільшень кутів повороту в шарнірах.
Реалізація закону керування (4.8) з використанням регулятора прямого каналу керування, що представляє собою інверсію робота,
здійснюється безпосередньою подачею в прямий канал керування необхідних сигналів положення - необхідний n-мірний вектор-стовпець збільшень кутів повороту в шарнірах.
Реалізація закону керування (4.8) з використанням регулятора прямого каналу керування, що представляє собою інверсію робота,
здійснюється безпосередньою подачею в прямий канал керування необхідних сигналів положення 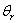 ,
швидкості ,
швидкості 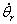 й прискорення й прискорення 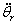 й множення їх на матриці
С, В и А відповідно. й множення їх на матриці
С, В и А відповідно.
4.1.2. Синтез регулятора зворотного зв'язку
Для підвищення стійкості замкнутої системи керування маніпулятором і поліпшення якості перехідних процесів використається регулятор
ланцюга зворотного зв'язку K(s):
де Kp і Kv - матриці (розмірністю n х n) коефіцієнтів зворотного зв'язку по положенню й швидкості, які
необхідно визначити. Закон керування, реалізований регулятором ланцюга зворотного зв'язку, має вигляд:
|
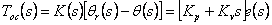
|
(4.10) |
або
|
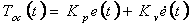
|
(4.11) |
де 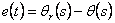 - n-мірний вектор збільшень помилки відстеження по положенню. Фактично рівняння
(4.11) являє собою закон управління каналу зворотного зв'язку по стані для лінеаризованой моделі (3.1) робота, оскільки воно
містить сигнали зворотного зв'язку як по - n-мірний вектор збільшень помилки відстеження по положенню. Фактично рівняння
(4.11) являє собою закон управління каналу зворотного зв'язку по стані для лінеаризованой моделі (3.1) робота, оскільки воно
містить сигнали зворотного зв'язку як по 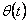 , так і по , так і по 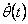 .
З огляду на результати вищенаведеного аналізу, побудуємо систему керування рухом у кінематичних парах "у збільшеннях", скомбінувавши
регулятор ланцюга зворотного зв'язку K(s) і регулятор прямого каналу керування
Q(s) як показано на блок - схемі мал. 4.2. .
З огляду на результати вищенаведеного аналізу, побудуємо систему керування рухом у кінематичних парах "у збільшеннях", скомбінувавши
регулятор ланцюга зворотного зв'язку K(s) і регулятор прямого каналу керування
Q(s) як показано на блок - схемі мал. 4.2.
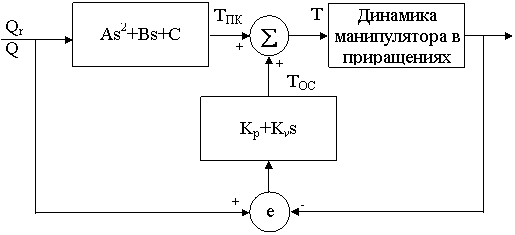
Рис. 4.2. - Система управління рухом маніпулятора в прирощеннях
З обліком мал. 4.2 закон руху в збільшеннях у частотній області задається в такий спосіб:
|
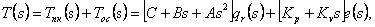
|
(4.12) |
або в тимчасовій області
|
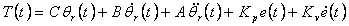
|
(4.13) |
Коли закон управління рухом у збільшеннях застосовується до нелінійної моделі маніпулятора,
"повний" закон керування задається вираженням:
|
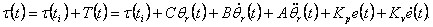
|
(4.14) |
Видно, що "повний" закон управління являє собою суму двох компонентів. Першої з них є значення вектора
моментів у кінематичних парах, прикладеного в номінальній робочій крапці Р, тобто
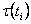 . Другий компонент обумовлений регуляторами K(s) і . Другий компонент обумовлений регуляторами K(s) і
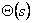 , що забезпечують керування рухом у збільшеннях. Нехай далі n - мірний
"повний" заданий вектор описується вираженням , що забезпечують керування рухом у збільшеннях. Нехай далі n - мірний
"повний" заданий вектор описується вираженням 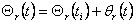 ,
a n-мірний "повний" вектор кутів повороту в шарнірах дорівнює ,
a n-мірний "повний" вектор кутів повороту в шарнірах дорівнює 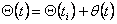 .
Підстановка цих виражень у рівняння (4.14) дає "повний" закон управління, певний через
"сумарні" змінні: .
Підстановка цих виражень у рівняння (4.14) дає "повний" закон управління, певний через
"сумарні" змінні:
|
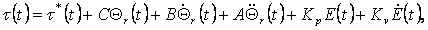
|
(4.15) |
де 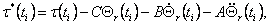 - n-мірний "сумарний" вектор помилки відстеження. Видно, що крім двох членів,
що відповідають регуляторам ланцюга зворотного зв'язку й прямого каналу керування, у повному законі керування (4.15) є
присутнім третій член - n-мірний "сумарний" вектор помилки відстеження. Видно, що крім двох членів,
що відповідають регуляторам ланцюга зворотного зв'язку й прямого каналу керування, у повному законі керування (4.15) є
присутнім третій член
|
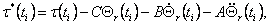
|
(4.16) |
відображаючий вплив положення робочої крапки Р.
4.2. Синтез алгоритмів керування промисловим роботом на основі дифеоморфного перетворення координат і нелінійного
зворотнього зв'язку за станом
Спочатку стабілізується нова лінійному й розімкнута по виході динамічна система. Потім для забезпечення стійкості
стабілізованої системи до невизначеностей у значеннях параметрів робота й завдання, додається контур оптимальної
корекції помилок для кожної лінійної підсистеми з розімкнутим виходом.
4.2.1. Стабілізація
Стабілізація здійснюється використанням контуру лінійного зворотного зв'язку F у системі й бажаному встановленні
полюсів замкнутої системи. Оскільки F є постійної блочно - діагональною матрицею, вся система залишиться лінійної
з розімкнутим виходом, називаної L&D - блоком (рис. 4.3). Для нового контуру зворотного зв'язку вводяться
лінійні ПД - регулятори:
|
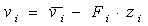
|
(4.17) |
де Fi=[fi1 fi2]. Тоді система (3.20) приймає вид:
|
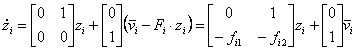 , ,
|
(4.18) |
Полюси кожної підсистеми визначаються вираженням:
|
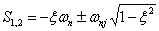 , ,
|
(4.19) |
де 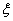 - коефіцієнт загасання; - коефіцієнт загасання; 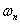 - власна частота;
- власна частота; 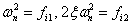 . .
Бажаний вхідний сигнал для кожної підсистеми можна одержати з рівнянь:
|
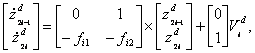 , ,
|
(4.20) |
|
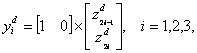 , ,
|
(4.21) |
де 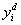 - бажана траєкторія. - бажана траєкторія.
4.2.2 Оптимізація помилок
Для синтезу оптимальної системи керування необхідно розглянути помилки
|
 , ,
|
(4.22) |
З рівнянь (4.18) - (4.22) можна одержати
|
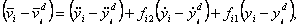 , ,
|
(4.23) |
тобто
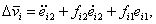
або
|
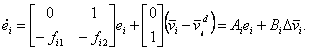 , ,
|
(4.24) |
У систему керування вводиться контур оптимальної корекції помилок, що забезпечує мінімізацію цільової функції
|
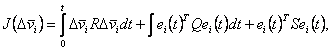 , ,
|
(4.25) |
де R - положительно-определенная матриця; Q и S - положительні-піввизначені матриці;
Т - час закінчення процесу. Відповідно до лінійної теорії оптимального керування оптимальна корекція
визначається вираженням:
|
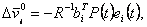 , ,
|
(4.26) |
де
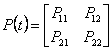
є положительно-определенной матрицею рішення рівняння Рікаті
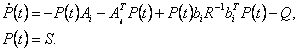
Якщо розглядати стале рішення при 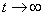 то то
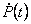 =0 і рівняння Рікаті приймає форму алгебраїчного рівняння: =0 і рівняння Рікаті приймає форму алгебраїчного рівняння:
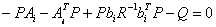
Звідси (4.27) приймає вид:
|
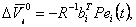 , ,
|
(4.27) |
або
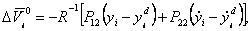
де
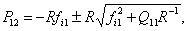
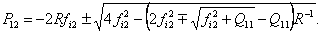
Структурна схема системи керування з оптимальною корекцією помилок представлена на рис. 4.3.
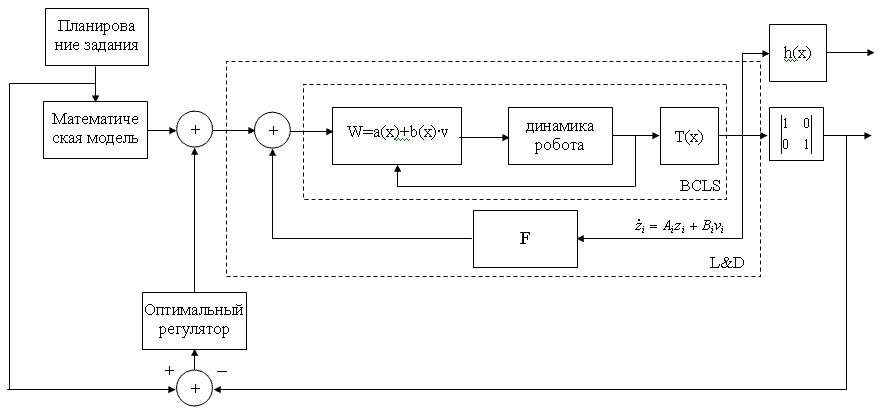
Рис. 4.3. - Система управління маніпуляційним роботом з дифеометричним регулятором
Угору
5. ЕКСПЕРИМЕНТАЛЬНА ПЕРЕВІРКА ПРАЦЕЗДАТНОСТІ СИНТЕЗОВАНИХ АЛГОРИТМІВ КЕРУВАННЯ НА ПЭВМ
З метою експериментальної перевірки працездатності синтезованих алгоритмів керування було проведене моделювання на ПЭВМ IBM PC.
Для цього розроблена програма в середовищі MATLAB. Проведення лінеаризації прогресивним методом, заснованим на застосуванні
теорії Чи груп вручну практично неможливо. Об'єктом моделювання є регулятор, побудований з використанням класичної теорії
багатомірних систем (багатомірний регулятор) і регулятор, синтезований на основі зазначеного новітнього методу керування.
Моделювання проведене у двох режимах: при відсутності (1 режим) і при наявності (2 режим) параметричних збурювань.

Рис 5.1. - Приклад роботи маніпулятора
Порівняльна оцінка експериментальних результатів моделювання рівнянь динаміки робота мінімальної конфігурації із синтезованими
багатомірним і дифеометричним регуляторами показує істотну перевагу алгоритмів керування, заснованих на новітньому методі. Так,
при значній зміні маси навантаження для новітнього методу помилка відстеження траєкторії не перевищила 0.1 мм, у той час як помилка
багатомірного регулятора перевищила 4 мм. При наявності в системі модельних помилок (відхилення параметрів моделі об'єкта на 50%)
багатомірний регулятор губить стійкість, дифеометричний регулятор при моделюванні в аналогічних умовах зберігає стійкість і необхідну
точність позиціювання (0.1 мм).
Угору
6.РОЗРОБКА АЛГОРИТМІВ КЕРУВАННЯ НА ОСНОВІ РОБАСТНИХ СИСТЕМ
Наступним етапом розробки системи є створення системи робастного керування, котра базується на сучасних формалізованих
підходах до математичного моделювання, дослідженню й проектованим системам. При розгляді адаптивних систем керування ми
прагнули до найкращого керування з погляду заданого критерію оптимальності. Адаптивна САУ, реагує в процесі функціонування
на зміну властивостей ОУ й зовнішніх впливів й, що пристосовується до нових умов на основі зміни структури й параметрів
керування пристроїв для того, щоб показник якості досягав екстремального значення.
Головним завданням синтезу робастних систем керування є пошук закону керування який зберігав би вихідні змінні системи й сигнали
помилки в заданих припустимих межах незважаючи на наявність невизначеностей у контурі керування. Невизначеності можуть приймати
будь-які форми, однак найбільш істотними є шуми, нелінійності, і неточності в знанні передатної функції об'єкта керування. Тому
подальша разроботка буде посвешена розробці робастного регулятора обеспечивающего роботу системи в умовах заданої невизначеності.
Угору
Список літератури
- Шахнипур М. Курс робототехники: Пер. с англ.- М.: Мир, 1990. - 527с.
- Фу К., Гонсалес Р., Ли К. Робототехника: Пер. с англ. М.: Мир, 1989. - 621с.
- Броккет Р. У. Алгебры Ли и группы в теории управления. Математические методы в теории систем. М.: Мир, 1979.
- Андреев Ю. Н. Дифференциально-геометрические методы в теории управления. Автоматика и телемехника 1982г. вып. 10.
- Системы очувствления и адаптивные промышленные роботы / В.Б. Брагин, Ю.Г. Войлов, Ю.Д. Жабитинский и др.;
Под общ. ред. Е.П. Попова, В.В. Клюева. - М.: Машиностроение, 1988. - 392с.
- Изерман Р. Цифровые системы упрвления: Пер. с англ. - М:Мир, 1984. - 541с.
- Уткин В.И Скользящие режимы в задачах оптимизации и управления. М.: Наука, 1981г. -368с.
- Y. L. Chen, Nonlinear feedback and computer control of robot arm, Ph. D. dissertation, Dept of System Science and Math.,
Washington Univ., St Louis, MO, Dec., 1984.
- Дьяконов В. Simulink 4. Специальный справочник.-СПб:Питер, 2002. - 528с.:ил.
- Дьяконов В. Круглов В. Математические пакеты расширения MATLAB. Специальный справочник.-СПб:Питер, 2001. - 480с.:ил.
|