Исходный URL: http://relpress.website.ru/currier/5/wavelet/wavelet.htm
Введение
В буквальном переводе с английского языка слово wavelet означает маленькая волна, такое название объясняется формой функций, используемых в вейвлет-анализе. Термин вейвлет-анализ по смыслу аналогичен термину Фурье-анализ. В обоих случаях речь идет о представлении исследуемого процесса в виде линейной комбинации различных функций, именуемых базисом соответствующего преобразования. Для вейвлет - анализа характерно понятие масштаб (scale), даже графическое представление в виде диаграммы специального вида именуется скейлограмма или скалограмма (scalogramm). Под масштабом следует понимать колебательные процессы различной периодичности. Будем говорить, что низкочастотные колебания имеют более крупный масштаб, а высокочастотные - более мелкий. Вейвлет - анализ называют микроскопом, поскольку он позволяет исследовать каждый масштаб с необходимой и достаточной для него разрешающей способностью. Как образно сказано в [2], можно увидеть и лес, и деревья¦.
1. Сопоставление вейвлет - преобразования и преобразования Фурье
Для преобразования Фурье (FT) базисом являются функции wn(t), полученные из функции w(t) = e i t = cos t + i sin t, путем масштабного преобразования wn(t) = w(nt). w(t) имеет период 2p. FT широко используется для спектрального анализа сигналов, однако имеет ряд недостатков: а) исходный сигнал заменяется на периодический, с периодом равным длительности исследуемого образца, б) FT плохо работает при изменении параметров процесса со временем (нестационарности), поскольку дает усредненные коэффициенты для всего исследуемого образца (см. рис.1-4.).
Рис.1 Исходные данные, представляющие сумму четырех синусоид одинаковой амплитуды и разной частоты. (данный рисунок взят из [2])
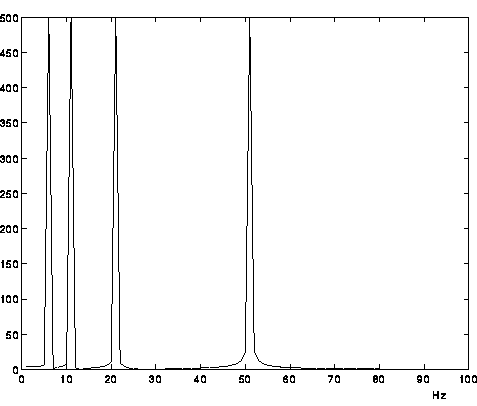
Рис.2 Преобразование Фурье для массива, представленного на рис. 1. (данный рисунок взят из [2])
Рис.3 Исходные данные, представляющие последовательность четырех синусоид одинаковой амплитуды и разной частоты. (данный рисунок взят из [2])
Рис.4 Преобразование Фурье для массива, представленного на рис. 3. (данный рисунок взят из [2])
Как видно из рис.4, FT не дает представления о динамике изменения спектрального состава сигнала, Фурье-образ на рис.4 - искаженный Фурье-образ рис.2, т.е. FT усредняет спектральные характеристики сигнала.
Вейвлет-преобразование (WT) в большой
степени позволяет преодолеть перечисленные недостатки FT,
поскольку базисные функции WT обладают свойством
временной локализации, т.е. обладают конечной энергией (нормой):
.
Как и для FT, для построения базиса WT используется одна функция, именуемая материнским вейвлетом (mother wavelet) - j(t). На рис.5 представлены примеры часто используемых вейвлетов: (а)WAVE, (б)MHAT - ?мексиканская шляпа¦, (в)Morlet - Морле, (г)Paul - Пауля, (д)LMB, (е)Daubechies - Добечи. Вейвлеты (в) и (г) являются комплексными.
Рис. 5 Временное представление некоторых вейвлетов и соответствующие им Фурье-образы. (рисунок взят из [1])
2. Построение базиса вейвлет-преобразования
Вейвлет-преобразование сигнала f(t) заключается
в разложении в виде 
, где y(t) - называют
отцовским вейвлетом, являющийся аналогом константы, а
{jjk(t)} - базис
WT, т.е. функции, полученные из материнского вейвлета
j(t) путем двух
основных операций: сжатие (scaling) и сдвиг
(shifting), при этом производится временное сжатие
в 
раз и сдвиг
полученной функции на 
: 
, например
Рис. 6 Преобразования вейвлета (рисунок взят из [4]) :
а) материнский вейвлет,
б) ?сжатый¦ (scaled) вейвлет,
в) ?сдвинутый¦ (shifted) вейвлет,
г) вейвлет, подвергнутый комбинированному преобразованию
(scaled and shifted).=
Вычислительная процедура дискретного WT (DWT) состоит в вычислении временной свертки сигнала с jjk(t). Поскольку длина вейвлета для каждого последующего масштаба уменьшается в 2 раза, для DWT используется вычислительная процедура, аналогичная быстрому преобразованию Фурье (БПФ). Для масштаба j=1 определяется 2 коэффициента: c10 и c11 , для j=2 - 4 коэффициента и т.д., поэтому вычислительный алгоритм DWT называют пирамидальным алгоритмом. Примеры DWT и его использования для фильтрации шумов приведены в [3,4,...]. Для удаления шума производят DWT, обрабатывают полученный образ и производят обратное вейвлет-преобразование (IDWT). Алгоритм IDWT аналогичен алгоритму DWT. Необходимым условием для возможности осуществить восстановление сигнала по его DWT путем обратного преобразования является ортогональность базиса. К ортогональным относится базис на основе вейвлета Добечи.
3. Непрерывное вейвлет-преобразование (CWT)
, где s -
масштаб.
Для анализа структуры сигналов удобно пользоваться отображением непрерывного WT (CWT - [2] ) на скейлограмме (scalogramm). Особенно выразительны скейлограммы для базисов, основанных на комплексных вейвлетах, в частности - на вейвлете Морле. При этом на скейлограмме отображается амплитуда преобразования - sqrt(Re[CWT(t,s)]^2+Im[Re(CWT(t,s)]^2). Поскольку вейвлет Морле - произведение действительной и мнимой экспоненты, кроме вейвлетов целочисленных масштабов, можно определить дробные масштабы, изменяя b и w:
На рис.6-9 преставленны скейлограммы реальных процессов - изменение цены закрытия акций Лукойл за различные периоды. На рис. 7 и 9 видны последствия финансового кризиса 28.10.97, для анализа больший интерес предствляют рис. 6 и 8. Масштаб на скейлограммах - выраженая в сутках длительность вейвлета.
Рис. 6
Рис. 7
Рис.8
Рис. 9
Список литературы и ссылки в Internet
На начало