Email:neptun@meganet.net.ua
Главную роль в развитии промышленности Украины играет топливно-энергетический комплекс. Функционирование и развитие топливно-энергетического комплекса Украины в значительной степени предопределяются состоянием и развитием угольной промышленности, которая широко распространена в нашем регионе.
В общем комплексе производственных процессов угольных шахт важное место занимают транспорт и подъем, который производится подъемными машинами и лебедками. Шахтные подъемные машины предназначены для оборудования шахтных подъемных установок вертикальных и наклонных стволов шахт, используемых для перемещения подъемных сосудов при подъеме полезных ископаемых и породы, спуске-подъеме людей, материалов, оборудования, ревизии и осмотре ствола, навеске и смене подъемных и уравновешивающих канатов.
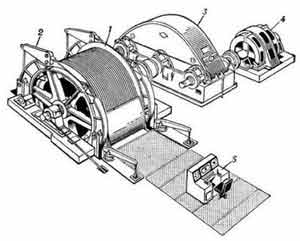
По назначению установки, различают: главные (для подъёма полезного ископаемого, а также породы на поверхность); вспомогательные (для подъёма и спуска людей и различных грузов); проходческие (при проходке и углубке стволов шахты) и инспекторские или аварийные (для ревизии ствола и подъёма людей в аварийных случаях). По типу подъёмных сосудов — клетевые, скиповые и бадьевые. По уравновешиванию массы подъёмных канатов: система неуравновешенная, статически уравновешенная и динамически уравновешенная. По типу органов навивки подъёмного каната: с постоянным радиусом навивки (цилиндрические барабаны, шкивы трения) и с переменным радиусом навивки (бицилиндроконические барабаны). На подъёмных машинах применяются электродвигатели мощностью до 5000 квт и более. Асинхронные электродвигатели переменного тока получили распространение на скиповых подъемных машинах мощностью до 1800—2000 квт и на клетевых, мощностью до 800—1000 квт. При больших мощностях подъёма обычно используются электродвигатели постоянного тока./1/ Данные установки широко применяются для перевозки людей, породы, материалов и оборудования. С помощью рассматриваемых установок транспортируется и уголь. При подъёме грузов технически и экономически рациональна максимальная скорость, как правило, до 20 м/сек, при подъёме людей — до 12 м/сек.
В работе Савина Г.Н., Горошко О.А., представлена динамика нити переменной длины. /2/ М. В. Петров в своей работе: “Уравнение динамики рудничного подъема с асинхронным двухдвигательным приводом”, представил уравнение динамики рудничного подъема для общего случая, а также получил уравнение динамики статически неуравновешенного рудничного подъема с двухдвигательным асинхронным электроприводом. Данные уравнения выведены для участка этапа замедления. По данной работе М. В. Петровым был сделан вывод в котором говорится, что закономерность замедления рудничного подъема с двухдвигательным асинхронным приводом в общем случае работы обоих двигателей на один вал не зависят от режима работы двигателей, за исключением режима свободного выбега статически уравновешенного подъема. От режима работы зависят только параметры уравнений. Режим свободного выбега статически уравновешенного подъема описывается уравнением второго порядка. Работы по расчетам рудничных подъемных установок проводил также Еланчик Г. М. Он является автором многих работ по рудничному и шахтному транспорту. Данные работы были изданы еще в 1941 году./6/ Он занимался такими вопросами, как выбор наивыгоднейших параметров проектируемой шахтной подъемной установки и др. Динамикой канатов занимались В. И. Дворников и А. В. Журба в своей работе: ”Динамические усилия в головных канатах многоканатных подъемных установок при загрузке скипа”. В данной работе рассматривается динамическое нагружение в период загрузки свободно висящего скипа, считая, что это нагружение является наиболее интенсивным и требующим особого внимания. “Достаточно сказать, что огромная масса угля или породы, достигающая 35 т, в течение нескольких секунд низвергается с высоты 10-15 м в кузов загружаемого сосуда, чтобы понять, насколько значительные динамические нагрузки испытывает канат в этот период рабочего цикла подъемной установки.” - говорится в работе./5/ Динамика каната рассматривается и в других работах В. И. Дворникова, а также М. Ю. Константинова, Н. И. Расторасова и др.
Для достижения вышеуказанной цели поставлены следующие задачи:
1. Выполнить обзор литературы
2. Ознакомиться с работами авторов, которые занимались данной проблемой
3. Составить математическую модель подъемной машины
4. Составить канонические уравнения и собственные формы колебаний
5. Решить эти уравнения, определив усилия во всех граничных сечениях каната
6. Разработать принципиальное устройство с демпфером колебаний
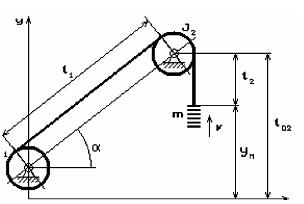
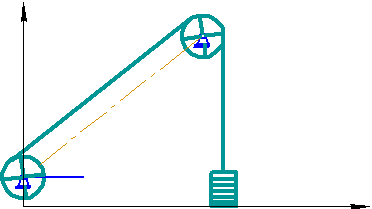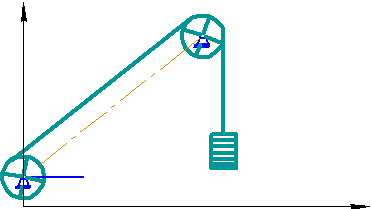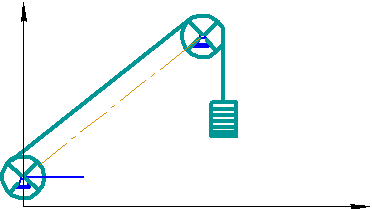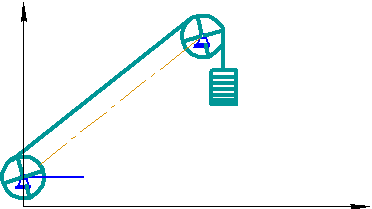
Здесь обозначено: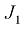
– кинетический момент инерции барабана машины с приведенными к нему моментами инерции вращающихся частей редуктора и ротора электродвигателя;
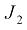– момент инерции направляющего (или копрового) шкива; 
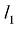– длина наклонной струны каната, считающейся постоянной во времени; 
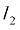– переменная длина отвесной части каната; 
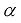– угол наклона струны; 
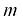– масса концевого груза; 
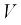– скорость подъема груза (здесь этот символ показывает всего лишь направление перемещений элементов системы); 
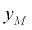– перемещение крюка подвески груза (подвесного устройства) по вертикали, отсчитываемое от некоторого исходного положения груза; 
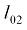– начальная длина отвеса каната в момент пуска двигателя (начало координат, точка O на рис. 2.1, может быть произвольной, но в зависимости от схемы подъема эта точка является вполне определенной). Пусть 
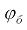и 
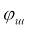– углы поворота барабана и шкива, отсчитываемые против часовой стрелки от некоторого исходного состояния. Предполагается также, что груз перемещается только в вертикальном направлении вдоль оси и не имеет боковых смещений (это может быть при наличии специальных проводников, вдоль которых перемещается груз). В таком случае алгебраическая разность
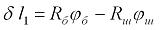2.1
есть величина упругого удлинения струны каната. В то же время
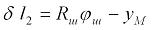2.2
есть, с точностью до несущественной константы, величина упругого удлинения отвеса каната. Здесь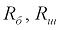 
– радиусы соответственно барабана и шкива.
Соотношения (2.1) и (2.2) дают возможность записать потенциальную энергию системы, «порождаемую» силами упругой деформацией каната, в следующем традиционном виде
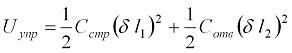2.3
где 
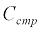и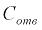 
– коэффициенты жесткости соответственно струны и отвеса каната, которые определяются следующим образом:
2.4
где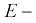 
модуль упругости стали проволоки; 
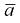– безразмерный параметр, зависящий от конструкции каната ; 
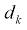– диаметр каната, .
Заметим, что в (2.4) в соответствии с рис. 2.1.
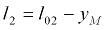2.5
но, строго говоря, 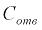зависит не от координаты 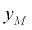, а от его «среднего значения» 
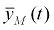, определяемого как средняя интегральная величина по времени 
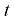при перемещении груза. Поэтому в дальнейшем переменную 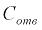в (2.4) следует рассматривать как параметрическую функцию от 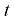, а не функцию от 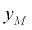. Итак, вместо (2.4) следует записать
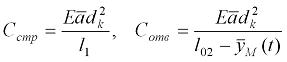2.6
По аналогии с этим массу отвеса каната определим как
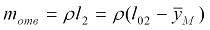2.7
причем здесь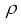 
– масса единицы длины каната, определяемая по формуле
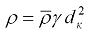2.8
где 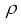– безразмерный параметр, зависящий от конструкции каната;
При записи потенциальной энергии, «порождаемой» гравитационными силами Земли, учтем, что центр тяжести отвеса каната можно определить с использованием (2.5) как
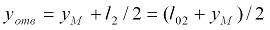2.9
то есть в данном случае предполагается, что все точки отвеса каната перемещаются синхронно и синфазно с перемещением концевого груза.
Разумеется, в действительности точки каната перемещаются по более сложному закону, и для описания таких перемещений требуется привлечение специальных методов математической физики. Однако с достаточной для инженерных целей точностью, в качестве, так сказать, первого приближения, вполне можно ограничиться представлением (2.9).
Что же касается центра тяжести струны каната, то он считается неизменяемым в пространстве, хотя на самом деле здесь остаются в силе высказанные выше соображения.
Итак, «гравитационная» часть потенциальной энергии с учетом (2.7) и (2.9) запишется в форме
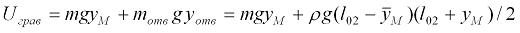
где g – ускорение свободного падения. А так как потенциальная энергия определяется с точностью до произвольной постоянной, то полученное выражение представим также в виде
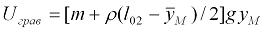2.10
Общая потенциальная энергия системы есть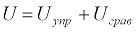 
, и подстановка сюда соотношений (2.10) и (2.3) с определениями (2.1) и (2.2) приводит к следующему окончательному выражению:
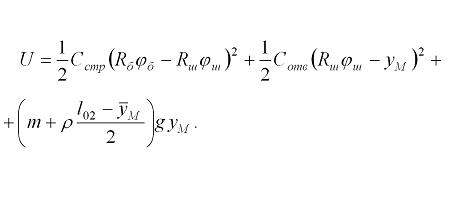2.11
Далее определим кинетическую энергию рассматриваемой системы, которая представляет собой сумму кинетических энергий совокупности двух вращающихся масс (барабана и шкива) и линейно перемещающихся масс концевого груза и каната. Массу части каната, навиваемой на барабан машины, присоединим к его вращающейся массе, то есть в таком случае фактический момент инерции барабана будет переменным и равным
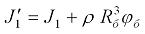2.12
В соответствии с этим выражением момент инерции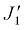 
формально являются функцией от переменной 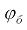. Однако практически 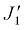зависит, по аналогии с определением 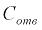в (2.4), не от координаты 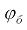, а от его «среднего значения» 
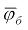, определяемого как средняя интегральная величина по времени 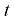при перемещении барабана. Поэтому в дальнейшем переменную 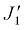следует рассматривать как параметрическую функцию от времени 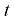, а не функцию от 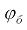, то есть вместо (2.12) следует записать
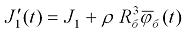2.13
Так как центр тяжести струны каната считается не перемещающимся в пространстве (кинетическая энергия струны каната в такой концепции является постоянной величиной, и ее, как известно, можно исключить из функции Лагранжа), а скорость центра тяжести отвеса каната в соответствии с (2.9) находится как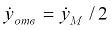 
(здесь и далее точка над символом динамической переменной означает ее производную по времени 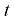), то в целом кинетическая энергия свободной (не навитой на барабан) каната с точностью до несущественной константы представляется в виде [с учетом (2.7)]
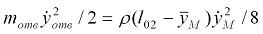
Тогда суммарная кинетическая энергия системы запишется как
2.14
и с помощью (2.11) и (2.14) можно записать функцию Лагранжа в виде
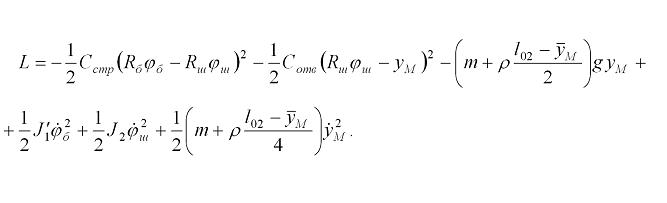2.15
В уравнениях Лагранжа второго рода
2.16
определим в качестве обобщенных координат элементов рассматриваемой установки переменные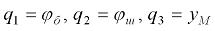 
и соответственно обобщенных скоростей – 
.
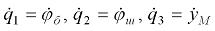Обобщенные непотенциальные силы 
для рассматриваемой системы в (2.16) примем следующими:
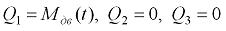2.17
где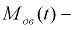 
приведенный к оси барабана момент, развиваемый двигателем, и эту переменную будем считать известной функцией от времени 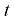(то есть в данном случае рассматривается так называемая вторая задача динамики системы подъема груза).
Обобщенные силы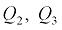 
приняты равными нулю, так как предполагается, что шкив и концевой груз не подвержены действию иных внешних сил, кроме уже учтенных. В действительности же на указанные тела действуют силы сопротивления воздушной среды, силы трения в подшипниковых узлах, возможно также возникновение каких либо импульсных нагрузок, вызванных, например, столкновением поднимающегося груза с препятствием и т.д. Однако такие силы здесь рассматриваться не будут.
Произведем необходимые вычисления производных от функции (2.15) в соответствии с формой записи уравнений Лагранжа (2.16). Прежде всего, вычислим частные производные по обобщенным координатам:
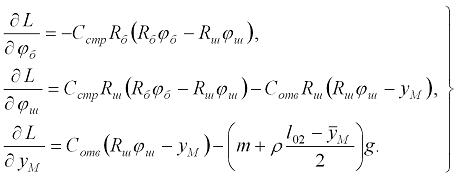2.18
Далее определим частные производные по обобщенным скоростям:
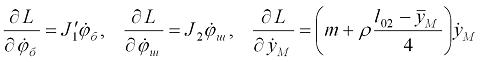
и возьмем полные производные по времени от этих величин:
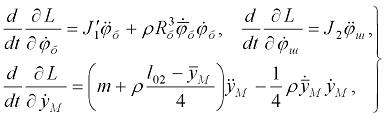2.19
причем в первом из этих выражений использовалось соотношение (2.13). Подставив теперь (2.18) и (2.19) в уравнение Лагранжа (2.16) с учетом (2.17), получим
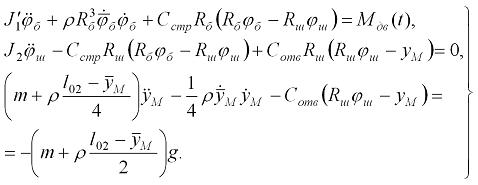2.20
Уравнения (2.20) и являются искомыми уравнениями, описывающие динамическое состояние подъемной машины или лебедки в рамках принятых, вполне оправданных допущений.
Важными переменными величинами являются не столько перемещения дискретных тел, сколько величины динамических нагрузок в упругих связях-канатах. Эти переменные параметры в связи с используемой концепцией при выводе уравнений (2.20) определяются следующим образом:
динамические усилия в струне каната –
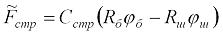
динамические усилия в отвесе каната –
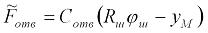
В дальнейшем планируется получить численные значения этих усилий, а также разработать демпфирующее устройство колебаний для этой системы
1. Завозин Л. Ф. Шахтные подъемные установки. Изд. 2-е переработ. И доп. М., «Недра», 1975, 368 с.
2. Савин Г. Н., Горошко О. А. Динамика нити переменной длины АН УССР Киев, 1962, 330 с.
3. Флоринский Ф.В. Динамика шахтного подъемного каната. Под ред. Савина Г. Н. М.: Углетехиздат, 1958 г. 239 с.
4. Нестерова П. П. Научные основы рационального проектирования и
эксплуатации элементов подъемного оборудования. К.: Н. Думка,
1978 г. 204 с.
5. Шахтный подъем. Сборник научных трудов №82 Донецк 1973 с. 90
6. Еланчик Г.М., Проходцева Е. А. Шахтные стационарные установки. МИРГЭМ, 1964
7. Павловский М.А. Теоретическая механика. Киев "Техника" 2002, 510 с.