УДК 621.646.94
Кононенко А.П., канд. техн. наук.
Донецкий национальный технический университет.
МОДЕЛЬ РАБОЧЕГО ПРОЦЕССА ЭРЛИФТА СО СНАРЯДНОЙ СТРУКТУРОЙ ВОДОВОЗДУШНОГО ПОТОКА
Розроблена математична модель робочого процесу ерліфту із снарядною структурою водопо-вітряного потоку в піднімальній трубі, що дозволяє визначати як кількісні гідродинамічні параметри двохфазної суміші, так і розрахункові характеристики піднімальника.
The mathematical model of the operating process of the airlift with the water-air flow slug structure in the lifting tunnel is developed. The model characterizes the two-phase mixture quantita-tive hydrodynamic parameters and the tunnel estimated performance.
1. Проблема и ее связь с научными и практическими задачами.
Достоверное математическое описание рабочих процессов гидравлических машин и аппаратов открывает возможности к повышению их надежности и эффективности. Создание адекватных моделей предполагает глубокое понимание происходящих гидродинамических явлений.
Водовоздушный поток в вертикальной подъемной трубе эрлифта реализуется в ряде структур (снарядной, эмульсионной, кольцевой), нестабильных в пространстве и во времени. Соз-дание единой теоретической модели для не-скольких структур газожидкостной смеси в настоящее время, из-за сложности процессов, не представляется возможным.
Поэтому математическое описание рабо-чего процесса эрлифта со снарядной структурой, как одной из наиболее часто реализуемых в подъемной трубе, является актуальной научной задачей, имеющей существенное практическое приложение.
2. Анализ исследований и публикаций.
Известные попытки описания снарядных струк-тур вертикальных двухфазных потоков в газо-жидкостном подъемнике носят, по заключению самого автора, больше качественный характер [1-2].
Развитие теории раздельного двухфазного течения, теории потока дрейфа [3-5] и много-численные экспериментальные данные [6-7] по-зволяют разрабатывать математические модели двухфазного снарядного течения, которое, по заключению многих видных ученых в области двухфазных потоков Кутателадзе С.С., Нигматулина Р.И., Уоллиса Г., Хьюитт Д. и др., является наиболее изученным и поддающимся количественному описанию.
Созданные модели снарядных течений применительно для конкретных условий – газ-лифтных скважин [8-9], горизонтальных трубо-проводов [10], пароводяных потоков в котель-ных установках [11-12], характеризуются свои-ми особенностями и не могут быть однозначно применены для расчета рабочего процесса в об-щепромышленном эрлифте.
3. Постановка задачи.
На основании существующей теории раздельного двухфазного течения и имеющихся эмпирических данных по сопротивлениям и истинным газосодержаниям необходимо разработать математическую модель рабочего процесса эрлифта со снарядной структурой водовоздушной смеси.
4. Изложение материала и результаты.
При снарядной структуре течения в эрлифте с подъемной трубой диаметром D, длиной H+h (H – высота подъема, h – геометрическое погруже-ние смесителя) и подающей трубой диаметром d газ движется с истинной скоростью .jpg) преимущественно в виде больших пузырей (снарядов) длиной L (рис. 1). Жидкостные пробки дли-ной LS, движущиеся с истинной скоростью
преимущественно в виде больших пузырей (снарядов) длиной L (рис. 1). Жидкостные пробки дли-ной LS, движущиеся с истинной скоростью  , как правило включают газовую фазу в виде мелких пузырей. Приведенная скорость водовоздушной смеси при этом
, как правило включают газовую фазу в виде мелких пузырей. Приведенная скорость водовоздушной смеси при этом  . В пристенной зоне имеет место нисходящее движение жидкостной пленки со скоростью
. В пристенной зоне имеет место нисходящее движение жидкостной пленки со скоростью 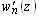 .
.
Уравнение стационарного восходящего движения водовоздушной смеси в вертикальной трубе для раздельного течения возможно пред-ставить в виде [3-5]

где р(z) – давление в сечении трубы на расстоянии z от смесителя;
 - касательное напряжение;
- касательное напряжение;
 - массовые скорости соответственно жидкости и газа;
- массовые скорости соответственно жидкости и газа;
 - плотность водовоздушной смеси;
- плотность водовоздушной смеси;
 - истинное газосодержание водовоздушной смеси;
g – ускорение свободного падения.
- истинное газосодержание водовоздушной смеси;
g – ускорение свободного падения.

Рис. 1. Схема эрлифта со снарядной структурой водовоздушного потока: истинная 1 и усредненная 2 эпюры давления в подъ-емной трубе
Массовые скорости газообразной img и жидкостной img фаз соответственно равны


где Qв – объемный расход воздуха при нормальных условиях;
Qэ – объемная подача эрлифта;
v – площадь сечения подъемной трубы;
 - плотность воздуха при нормальных усло-виях;
- плотность воздуха при нормальных усло-виях;
 - плотность воды;
x – массовое расходное газосодержание;
G – массовая скорость водовоздушной смеси.
- плотность воды;
x – массовое расходное газосодержание;
G – массовая скорость водовоздушной смеси.
Плотность смеси  в модели раздельного течения описывается выражением
в модели раздельного течения описывается выражением

где - плотность воздуха в сечении z.
- плотность воздуха в сечении z.
Подставим в уравнение движения (1) значения переменных в соответствии с (2), (3) и (4) и преобразуем его учитывая, что массовая ско-рость водовоздушной смеси G величина постоянная

Действительные скорости фаз в подъем-ной трубе:
• воды

• воздуха

При допущении линейности изменения давления по высоте абсолютное давление в сечении z подъемной трубы

где р0 – атмосферное давление; рсм – избыточное давление в смесителе.
При z = 0 абсолютное давление в смесителе .

Объемный расход воздуха в z-ом сечении подъемной трубы при изотермическом процессе изменения состояния газовой фазы

Проинтегрируем выражение (5) для участка подъемной трубы эрлифта длиной zi (где 0 zi H+h)

Из (7) с учетом (6) получим

Уравнение (8) представим в виде

где  - суммарный перепад давления на участке подъемной трубы длиной zi,
- суммарный перепад давления на участке подъемной трубы длиной zi,

а составляющие правой части зависимости (9) выражают:
• перепад давления на участке подъемной трубы длиной zi, обусловленный трением

• перепад давления на участке подъемной трубы длиной zi, обусловленный ускорением

• перепад давления на участке подъемной трубы длиной zi, обусловленный силой тяжести

Касательные напряжения  и истинные газосодержания f вычисляются по эмпирическим выражениям, рекомендованным для вертикальных восходящих газожидкостных потоков [5-7, 10, 13].
и истинные газосодержания f вычисляются по эмпирическим выражениям, рекомендованным для вертикальных восходящих газожидкостных потоков [5-7, 10, 13].
Средний объемный расход водовоздушной смеси на участке подъемной трубы длиной zi

Суммарная мощность, необходимая для компенсации потерь на трение, ускорение и гравитационной составляющей при движении водовоздушного потока со средним объемным расходом Qсрi по участку вертикальной подъемной трубы длиной zi с учетом (10) и (14)

Мощность, необходимая для компенсации потерь на трение на участке подъемной трубы длиной zi с учетом (11) и (14)

Мощность, необходимая для компенсации потерь на ускорение на участке подъемной тру-бы длиной zi с учетом (12) и (14)

Мощность, необходимая для преодоления силы тяжести при движении водовоздушного потока со средним объемным расходом Qсрi на участке подъемной трубы длиной zi с учетом (13) и (14)

Суммарная мощность (15) складывается из составляющих (16), (17) и (18)

Мощность, подведенная на участке трубы длиной zi потоком сжатого воздуха

Мощность, подведенная к подъемной трубе потоком воды

Мощность, подведенная на участке подъемной трубы длиной zi водовоздушным потоком, определяется суммой значений (20) и (21)

Для случая zi
Мощность, необходимая для компенсации потерь на скольжение фаз при движении водовоздушного потока на участке трубы длиной zi

Решение уравнений (9), (19) и (22) численным методом на ПЭВМ при помощи разработанной программы позволяет определять следующие количественные значения и зависимо-сти (с графическим построением):
а) значения текущих гидродинамических параметров водовоздушной смеси в заданных сечениях подъемной трубы и при заданном расходе воздуха Qв;
б) зависимость подачи эрлифта Qэ от расхода воздуха Qв (построение расходной характе-ристики);
в) изменение давлений 
 и мощностей
и мощностей  по высоте подъемной трубы и в зависимости от расхода воздуха Qв.
по высоте подъемной трубы и в зависимости от расхода воздуха Qв.
Адекватность разработанной математической модели рабочего процесса эрлифта со снарядной структурой водовоздушного потока подтверждается удовлетворительной сходимостью расчетных количественных значений гидродинамических параметров с экспериментальными данными (рис. 2).

Рис 2. Экспериментальная 1 и расчетная 2 расходные характеристики эрлифта D = 50 мм, H+h = 14,0 м, h = 5,5 м
5. Выводы и направление дальнейших исследований.
Разработана модель рабочего процесса эрлифта со снарядной структурой водовоздушного потока в подъемной трубе, позволяющая определять количественные значения гидродинамических параметров двухфазной смеси и получать расходные и мощностные характеристики подъемника. Достоверное математическое описание рабочего процесса эрлифта позволит уточнить способы повышения его энергетической эффективности.
Список литературы.
1. Пирвердян А.М. Теоретические основы подъема жидкости сжатым воздухом. Азербайджанское нефтяное хозяйство, N1, 1951, с. 16-19.
2. Пирвердян А.М. Физические основы подъема жидкости сжатым воздухом. Азербай-джанское нефтяное хозяйство, N10, 1951, с. 4-7.
3. Кутателадзе С.С., Стырикович М.А. Гидродинамика газожидкостных систем. 2-е изд., перераб. и доп. - М.: Энергия, 1976, - 296 с.
4. Нигматулин Р.И. Динамика многофаз-ных сред. ч. ??. – М.: Наука, Гл. ред. физ.мат. лит., 1987. – 360 с.
5. Уоллис Г. Одномерные двухфазные те-чения. М.: Мир, 1972. – 440 с.
6. Арманд А.А. Исследование механизма движения двухфазной смеси в вертикальной трубе. В кн.: Гидродинамика и теплообмен при кипении в котлах высокого давления. М.: Изд-во АН СССР, 1955, с. 21-34.
7. Исследование турбулентных течений двухфазных сред/ Под ред. Кутателадзе С.С., Новосибирск, 1973. – 315 с.
8. Маркович Э.Э. Образование и длина жидких пробок в газлифтных скважинах. Неф-тяное хозяйство, 1991, N12, с.22-23.
9. Айтемиров З.А. Некоторые вопросы движения пробковой структуры газонефтяного потока. Изв. ВУЗов, Нефть и газ, 1969, N8, с. 39-41.
10. Движение газожидкостных смесей в трубах / Мамаев В.А., Одишария Г.Э., Клапчук О.В., Точигин А.А., Семенов Е.И. М.: Недра, 1978. – 271 с.
11. Субботин В.И., Похвалов Ю.Е., Ми-хайлов Л.Е., Кронин И.В., Леонов В.А. Времен-ные и структурные характеристики газожидко-стного потока при снарядном течении. Тепло-энергетика, 1976, N1, с.67-70.
12. Субботин В.И., Похвалов Ю.Е., Леонов В.А. Структура снарядного пароводяного пото-ка. Теплоэнергетика, 1977, N7, с.65-67.
13. Гриценко А.И., Клапчук О.В., Харчен-ко Ю.А. Гидродинамика газожидкостных смесей в скважинах и трубопроводах. М.: Недра, 1994. – 238 с.
.jpg) преимущественно в виде больших пузырей (снарядов) длиной L (рис. 1). Жидкостные пробки дли-ной LS, движущиеся с истинной скоростью
преимущественно в виде больших пузырей (снарядов) длиной L (рис. 1). Жидкостные пробки дли-ной LS, движущиеся с истинной скоростью  , как правило включают газовую фазу в виде мелких пузырей. Приведенная скорость водовоздушной смеси при этом
, как правило включают газовую фазу в виде мелких пузырей. Приведенная скорость водовоздушной смеси при этом  . В пристенной зоне имеет место нисходящее движение жидкостной пленки со скоростью
. В пристенной зоне имеет место нисходящее движение жидкостной пленки со скоростью 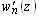 .
.
 - касательное напряжение;
- касательное напряжение;
 - массовые скорости соответственно жидкости и газа;
- массовые скорости соответственно жидкости и газа;
 - плотность водовоздушной смеси;
- плотность водовоздушной смеси;
 - истинное газосодержание водовоздушной смеси;
g – ускорение свободного падения.
- истинное газосодержание водовоздушной смеси;
g – ускорение свободного падения.



 - плотность воздуха при нормальных усло-виях;
- плотность воздуха при нормальных усло-виях;
 - плотность воды;
x – массовое расходное газосодержание;
G – массовая скорость водовоздушной смеси.
- плотность воды;
x – массовое расходное газосодержание;
G – массовая скорость водовоздушной смеси.
 в модели раздельного течения описывается выражением
в модели раздельного течения описывается выражением
 - плотность воздуха в сечении z.
- плотность воздуха в сечении z.








 - суммарный перепад давления на участке подъемной трубы длиной zi,
- суммарный перепад давления на участке подъемной трубы длиной zi,



 и истинные газосодержания f вычисляются по эмпирическим выражениям, рекомендованным для вертикальных восходящих газожидкостных потоков [5-7, 10, 13].
и истинные газосодержания f вычисляются по эмпирическим выражениям, рекомендованным для вертикальных восходящих газожидкостных потоков [5-7, 10, 13].










 и мощностей
и мощностей  по высоте подъемной трубы и в зависимости от расхода воздуха Qв.
по высоте подъемной трубы и в зависимости от расхода воздуха Qв.