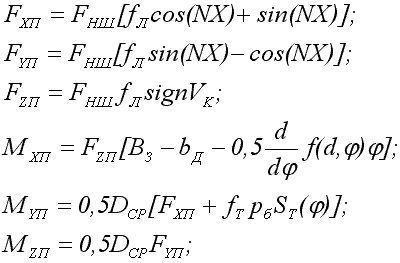
1. Кондрахин В. П. «Имитационная математическая модель динамических процессов очистных комбайнов высокой энерговооруженности с вынесенной системой подачи» / В.П. Кондрахин, В.Г. Гуляев, В.Л. Головин // Наук. пр. Донец. нац. техн. ун-ту.-Донецьк, 2006.-С.123-130.- (Сер. : гірничо-електромеханічна; Вип.12(113) )

   Проблема и ее связь с научными и практическими задачами.
   Существующие имитационные математические модели (ММ), адекватность которых подтверждена результатами экспериментальных исследований, позволяют решать задачи оптимизации очистных комбайнов (ОК) на всех этапах их создания и в различных режимах работы. Эти ММ основываются на фундаментальных методологических положениях теории работы очистных комбайнов как сложных нелинейных динамических систем, подверженных действию детерминированных и случайных возмущений.
   Следует сказать, что указанные ММ создавались для комбайнов, компоновочные схемы, конструкция и параметры которых не в полной мере соответствуют современным требованиям. За последние го-ды институтом ГП «Донгипроуглемаш» на базе машиностроительного завода ЗАО “Горловский машиностроитель” создан целый ряд добычных комбайнов современного технического уровня [1] для широкого спектра горно-геологических условий (УКД200-250, УКД300, КДК500 и др.). Для этих машин характерна увеличенная в 2-3 раза энерговооруженность по сравнению с серийными комбайнами, что обусловливает интенсификацию их рабочих режимов, проявляющуюся в интенсивных колебаниях корпусной и других подсистем.
   Известные ММ могут быть успешно использованы для структурно-параметрической оптимизации новых комбайнов только после их уточнения, корректировки и дальнейшего совершенствования. Поэтому разработка и адаптация ММ применительно к ОК современного технического уровня, в частности для широко распространенно-го комбайна УКД200-250 (на шахтах Украины и России в 2006 году работало 16 таких машин) с вынесенной системой перемещения, яв-ляется актуальной проблемой.

   Анализ исследований и публикаций.
    Исследованиям, изучению, анализу и оптимизации рабочих процессов ОК посвящено значительное количество научных работ. Для решения рассматриваемой проблемы особый интерес представляют исследования в области динамики и устойчивости ОК с вынесенной системой подачи [2], специфических условий работы шнековых исполнительных органов для отработки тонких пластов [3]. При этом достаточно широко могут быть использованы разработанные и апробированные подходы при создании ММ для описания различных процессов функционирования комбайнов [4, 5, 6 и др.].
   Постановка задачи. Задачей настоящей работы является разработка имитационной математической модели, комплексно описывающей процессы функционирования очистного комбайна с вынесенной системой подачи типа УКД200-250 при высокоинтенсивных режимах работы.

   Изложение материала и результаты.
   При разработке имитационной ММ важно обеспечить ее максимально достижимое соответствие реальным (как установившимся, так и переходным) процессам функционирования ОК. Особенность данной ММ состоит в том, что в ней впервые комплексно учитываются все основные факторы, имеющие важное значение при моделировании высокоинтенсивных режимов работы системы «ОК для выемки тонких пластов – забой»:
- внешние связи в системе «ОК – забой», причем для нахождения мгновенной толщины стружки на каждом резце использована математическая модель, учитывающая осевые перемещения исполнительного органа [7];
- перемещения корпусной подсистемы комбайна по всем 6-ти степеням свободы и ее внутренние динамические связи с подсисте-мой подвески и регулирования исполнительных органов;
- сопротивление от погрузки угля шнековыми исполнительными органами;
- переходные электромагнитные процессы в приводном электродвигателе с использованием уравнений Парка-Горева [8].
При разработке модели использован апробированный метод моделирования мгновенных значений проекций вектора внешних возмущений (ВВВ) от разрушения пласта [4].
   Сопротивление от погрузки угля очистными комбайнами для тонких пластов играет важную роль в формировании нагрузок комбайна, поскольку процесс выноса продуктов разрушения из призабойного пространства и их погрузки на конвейер происходит в силовом режиме. При этом определение силовых и энергетических параметров комбайна производится с учетом следующих составляющих ВВВ от погрузки [3]:

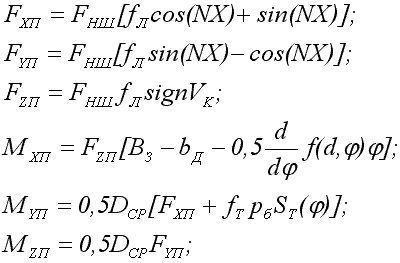
   На рис. 1 представлена эквивалентная расчетная схема, для математического описания которой использованы системы координат – основная (OXYZ) и две вспомогательные (O/X/Y/Z/ и O//X//Y//Z//). Начало отсчета основной системы лежит на середине опорной базы ОК (по координате х), а его координаты y и z совпадают с соответствующими координатами центра масс комбайна. Начала координат вспомогательных систем лежат на осях шарнирных соединений основных и поворотных редукторов в точке их пересечения с завальной плоскостью корпуса машины. На схеме указаны положительные направления обобщенных координат q_S, центры масс О_i составных частей комбайна, направление скорости подачи V_п.
   Для составления дифференциальных уравнений, описывающих динамические процессы в указанной автономной системе, воспользуемся уравнениями Лагранжа II рода для системы со стационарными связями:

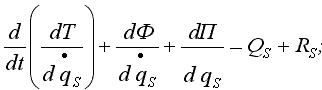
где   R_S – реакции неголономных связей;
          q_S, Q_S – соответственно обобщенная координата и обобщенная сила с порядковым номером s=1…11;
          q₁ – перемещение центра масс ОК вдоль конвейера (по оси OX);
          q₂ – перемещение центра масс ОК по нормали к конвейеру (по оси OZ);
          q₃ – перемещение центра масс ОК вдоль оси OY;
          q₄ – угловое перемещение ОК (“потаптывание”) относительно оси OX;
          q₅ – угловое перемещение ОК (“рыскание”) относительно оси OZ;
          q₆ – угловое перемещение ОК (“галопирование”) относительно оси OY;
          q₇ – угловое перемещение левого поворотного редуктора относительно оси O//Y//;
          q₈ – угловое перемещение правого поворотного редуктора относительно оси O/Y/;
          q₉ – угловое перемещение левого шнека относительно оси приводного вала;
          q₁₀ – угловое перемещение правого шнека относительно оси приводного вала;
          q₁₁ – угловое перемещение сосредоточенной массы ротора ЭД;
          T, П – кинетическая и потенциальная энергия системы;
          Ф – диссипативная функция системы.