Л. Левкович-Маслюк, А. Переберин Биортогональные вейвлеты, вейвлет-пакеты, сжатие изображений
Ссылка: http://algolist.manual.ru/compress/image/leo_lev/lecture2/wav2_1.php
Построение ОМА с гладкими базисными функциями сводится к построению тригонометрических многочленов, удовлетворяющих (1.2’) и ряду дополнительных ограничений (не любая пара QMF порождает ОМА). Найдя такой многочлен (т.е. набор коэффициентов hk), можно вычислить скейлинг-функцию и вейвлет с любой точностью из (2.1) и (2.2). Однако, как выяснилось, класс таких многочленов довольно узок, что накладывает на свойства фильтров неудобные ограничения. В частности, они не могут быть симметричными. Сейчас мы очень коротко наметим классический метод построения таких фильтров, принадлежащий Ингрид Добеши (Ingrid Daubechies).
Обозначим
 . Должно выполняться условие:
. Должно выполняться условие:
Ищем решение в виде:
 , – многочлен. Тогда
, – многочлен. Тогда  . Положим y=cos2omega/2, тогда
. Положим y=cos2omega/2, тогда
 (2.4) ,
(2.4) ,и (2.3) превращается в
 (2.5)
(2.5)
Требуется: а) найти многочлен P(y), удовлетворяющий (2.5) и такой, что
 при 0<=y<=1, и б) извлечь из него квадратный корень в смысле (2.4). Ответ на а) предъявляется:
при 0<=y<=1, и б) извлечь из него квадратный корень в смысле (2.4). Ответ на а) предъявляется:
 (2.6)
(2.6)(это фактически единственное решение). Ответ на б) также дается явным выражением, которое мы из-за громоздкости не приводим. В него входят комплексные корни многочлена от z, который получается из (2.6) при выражении через y=sin2omega/2. При выборе различных подмножеств множества корней получаются фильтры с различными свойствами. Показатель N в (2.5) определяет степени полиномов, которые “убиваются” разложением по построенному таким образом вейвлет-базису:

Эта величина называется количеством нулевых моментов (number of vanishing moments). В классической конструкции Добеши длина фильтров 2N, а количество нулевых моментов N. На практике это означает, что фильтр g подавляет полиномиальную составляющую сигнала вида
 , которая остается только в крупномасштабной версии. Например, для вейвлетов Хаара
, которая остается только в крупномасштабной версии. Например, для вейвлетов Хаара  , и применение фильтра убивает постоянную составляющую сигнала.
, и применение фильтра убивает постоянную составляющую сигнала.
Существует более гибкая конструкция МА, где класс допустимых фильтров шире, их коэффициенты проще вычислить, они могут быть симметричными и обладать другими полезными свойствами. Это – биортогональный МА, БМА. Быстрый алгоритм Малла сохраняется, но при разложении и восстановлении используются разные пары фильтров. Каждой паре соответствует МА со своими скейлинг-функцией и вейвлетом. Но эти МА не ортогональны – сдвиги скейлинг-функций и вейвлетов не ортогональны друг другу. Поэтому преобразования (1.8) – (1.9) не ортогональны. (Это означает, между прочим, что погрешность, внесенная при сжатии, может увеличиваться при восстановлении). Рассмотрим две пары фильтров: (h,g) и
 . Мы хотим проводить разложение при помощи свертки с
. Мы хотим проводить разложение при помощи свертки с 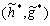 , а восстановление – при помощи (h,g).
, а восстановление – при помощи (h,g).
Запишем условия точного восстановления (см. начало лекции 1). В терминах -преобразования разложение на высокие и низкие частоты с прореживанием вдвое имеет вид:

Записав в аналогичном виде процесс восстановления с помощью пары , приравняв результат к , и подставив , получим условия на ДПФ искомых фильтров (аналог (1.2)):

Вводя матрицы
 ,
,
 (2.7’)
(2.7’) Посмотрим на скейлинг-функции, получаемые из этих фильтров. Напишем уравнения вида (2.1):
 (2.8)
(2.8) Их решения ищутся при помощи такого итерационного процесса (см. рис. 3 из лекции 1): сначала в правую часть подставляется единичная ступенька (скейлинг-функция Хаара), затем – результат этой подстановки, сжатый вдвое по , и т.д. Мы видели, что предельная функция определяет ОМА только если имеет очень специальный вид (см. 2.3 – 2.6). Для БМА выбор возможных фильтров шире, но тоже требуются дополнительные условия, при которых имеет место сходимость итераций, а предельные функции образуют базис.
Как и в ортогональном случае, должны выполняться некоторые дополнительные условия (которые мы здесь не уточняем), гарантирующие сходимость, регулярность и базисность решений уравнений рескейлинга (2.8) – (2.9). Кроме того, желательно, чтобы вейвлет, используемый для разложения, имел хоть несколько нулевых моментов, а вейвлет и скейлинг-функция, используемые для восстановления были как можно более гладкими. Имеется решение, удовлетворяющее всем этим требованиям. Это решение использует сомножители того тригонометрического многочлена, который был использован для построения ОМА (см 2.5).
Для увеличения разрешения вейвлет-фильтров по частоте используется простой, красивый и эффективный прием. Опишем его для ортогонального случая. Напомним, что при работе алгоритма Малла на каждом шаге “отрезается” половина (в случае идеального фильтра) низкочастотной части диапазона. Но ведь можно применить ту же операцию “расщепления” (splitting) к любой из получающихся высокочастотных компонент. На рисунке 1 слева показана схема алгоритма Малла, справа – другая схема разложения сигнала, при которой каждый высокочастотный диапазон из схемы Малла тоже делится пополам.

Рисунок 1 - Разложение по вейвлет-пакетам
Дерево на рис. 1 справа соответствует замене вейвлета на два новых вейвлета:
 и
и  . Теперь разложение
. Теперь разложение  превращается в
превращается в  , где W1j и W2j порождены соответственно
, где W1j и W2j порождены соответственно  и
и  . Новые вейвлеты тоже локализованы в пространстве, но на вдвое более широком отрезке, чем исходный вейвлет, так как их локализация по частоте вдвое тоньше.
. Новые вейвлеты тоже локализованы в пространстве, но на вдвое более широком отрезке, чем исходный вейвлет, так как их локализация по частоте вдвое тоньше.
Можно нарисовать произвольное бинарное дерево разложения, и ему будет соответствовать набор подпространств с базисами, построенными по аналогичному рецепту. Функции, порождающие эти базисы, и называются вейвлет-пакетами (wavelet-packets). Ясно, что та же схема действует и в биортогональном случае.
На практике (при сжатии данных, например) мы имеем дело только с фильтрами. За счет выбора оптимального дерева для данного сигнала или класса сигналов иногда можно существенно (в несколько раз) повысить эффективность сжатия. Для выбора [квази]оптимального дерева разработан ряд методов. Все они основаны на введении некоторой функции (“энтропии”), позволяющей оценить “информативность” набора коэффициентов. Стратегия такова: сначала строится полное дерево разложения, затем снизу вверх анализируются пары узлов, имеющих общий корень. Если при переходе от корня к узлам энтропия не уменьшается, эта пара заменяется на корень. Упрощенный вариант – подобрать оптимальный уровень, т.е. высоту полного дерева, при которой энтропия минимальна.
- I. Daubechies. Ten Lectures on Wavelets. SIAM, 1992.
- C.K.Chui. Wavelets: a tutorial in theory and applications, Academic Press, 1992. IEEE Trans. on Information Theory, Vol. 38, No. 2, March 1992 (специальный номер по вейвлетам)
- A. Said, W.Pearlman, A New Fast and Efficient image Codec Based on Set Partitioning in Hierarchical Trees, IEEE Trans. on Circuits and Systems for Video Technology, V.6, June 1996.