AbstractSmirnov A.V., Gurjanova T.V. Article "RalfWins's "optimal f "about". Lacks of the ft Wins theory of optimal f (optimal part of reinvested profits) are disclosed. The margins of practical applicaion the theory are found. They depends on volume of used statistics transaction results, features of average profit; sizes calculation and theirs variance under condition of normal distribution of random values P&L. ВведениеГлавная задача экономической кибернетики как науки заключается в реализации эффективного управления различными экономическими системами. С вступлением Украины в ВТО эта задача становится еще более актуальной, поскольку интеграция в международные торговые институты ни коим образом не уменьшает жесткой конкуренции между субъектами предпринимательской деятельности. Качественное управление инвестиционными портфелями, компьютерными торговыми системами и другими объектами, к сожалению, в Украине еще ведется не на должном уровне. Вместо этого используется пресловутое «организационное управление», эффективность которого определяется. в основном, субъективными характеристиками руководителя. Для повышения эффективности экономических систем часто производится реинвестирование полученной прибыли в новые инвестиционные проекты млн в расширение старых. Это позволяет получить дополнительный экономический эффект, который сопровождается одновременным увеличением инвестиционного риска. Американский ученый Р. Винс разработал свою теорию «оптимального f» - оптимальной части капитала, которую следует реинвестировать для умножения первоначального капитала инвестора в необходимое число раз за кратчайшее время.[1] Однако, из-за существенных математических некорректностей, грубых допущений, практическое использование теории «оптимального f » Р. Винса вызывает много вопросов и весьма рискованно. Цель исследованийЦелью настоящих исследований является нахождение границ применимости «оптимального f» Р. Винса на практике в зависимости от статических характеристик управляемых экономических систем. К сожалению, автор этой теории не обратил внимания на то, что алгоритм нахождения fопт представляет собой нелинейное стохастическое уравнение. При его решении относительно fопт часто возникают нелинейные эффекты, которые могут ввести в заблуждение инвестора и привести к большим финансовым потерям. Основными задачами данных исследований является нахождение причин, приводящих теорию «оптимального f > г Р. Винса к некорректным результатам на практике, и их устранение. Основные соотношения теории «оптимального f»Здесь и далее сохраняются как терминология Р. Винса, так и принятые им в [1] обозначения. «Прибыль за период удержания позиции» (holding period returns} обозначается как HPR. Выигрыш или проигрыш компьютерной торговой системы, трейдера или портфельного менеджера - это P&L . Если выигрыш, то HPR = 1 + Р &L, а в случае проигрыша имеем HPR = 1 - Р & L . Между средним арифметическим и средним геометрическим показателями эффективности экономической системы существует соотношение (1): G = AHPR^2-SD^2 (1),
В случае с реинвестированием прибыли, среднее геометрическое экономической системы нагляднее отображает ее качество по сравнению с AHPR. Отношение между конечным и начальным состоянием счета инвестора обозначается как TWR (Terminal Wealth Relative). По своей сути TWR - это множитель первоначальной суммы на счете (если, например, TWR = 10,55, то первоначальный счет инвестора вырос в 10,55 раз или же на 955%). Между TWR и HPR имеется следующая взаимосвязь: TWR = П HPR (2) Среднее геометрическое экономической системы определяется как:
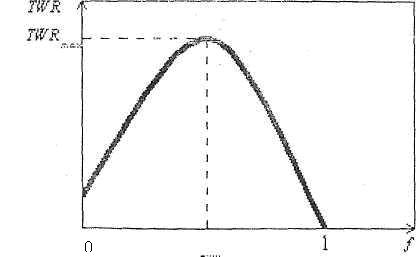
Без достаточно строгих математических доказательств путем рассуждений Р. Винc вводит понятие части капитала инвестора f, которая, по мнению автора, является «оптимальной f» для TWRmax (рис.1). Путем последовательного перебора всех значений f в диапазоне 0 < f < 1 с достаточно малым шагом (например, с шагом 0,01) находится fопт [1]:
где: f - часть капитала для реинвестирования (искомая характеристика экономической системы); (-Р & Li)- убытки или выигрыши, взятые с противоположными знаками; (Р & L)jmin - самый значительный убыток (всегда берется со знаком минус); fопт - одно из значений f, при котором TWR = TWRmax.
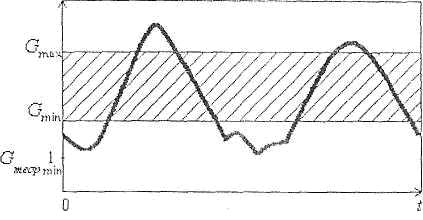
Рисунок 1 – К понятию «оптимальное f» Таким образом, имея статистику выигрышей и проигрышей объемом п, можно найти fопт, при которой TWR максимален. Этим самым существенно повышается качество экономической системы с реинвестированием. Недостатки теории «оптимального f»Проведенные нами исследования позволяют выделить следующие существенные недостатки рассматриваемой теории, которые ограничивают ее применение на практике. 1. Теория «оптимального f» строго справедлива для оценки качества экономической системы с реинвестированием в прошлом и дает посредственные результаты при ее использовании для практического оперативного управления. Это связано с тем, что даже при фиксированных значениях AHPR и SD^2, величины fопт будут меняться от выборки к выборке при n = const. Следовательно, нужно использовать интервальную оценку fопт . В этой связи вызывают сомнение понятия, предложенные Р. Винсом, - «дробные fопт и «минимальное время для достижения TWR». Эти характеристики представляются нам достаточно грубыми, поскольку они не учитывают реальных величин интервальных оценок fопт. 2. К сожалению. Р. Винс не нашел границ практической применимости (4) в зависимости от закона распределения случайных величин Р & Lt, объема выборки n и величин AHPR, SD2. В своих исследованиях он ввел только нижнюю теоретическую границу Gтеорmin = 1 , Тем самым. как будет показано ниже, инвестор многим рискует, применяя (1) - (4) для практического нахождения fопт . При этом он может получить вместо выигрыша по TWR значительное его уменьшение вплоть до проигрыша при реинвестировании. На рис.2 показана гипотетическая траектория G(t) экономической системы. Здесь в заштрихованной рабочей области G теория Р. Винса применима с заданной доверительной вероятностью Р , а вне ее -возможны серьезные потери средств инвестора.
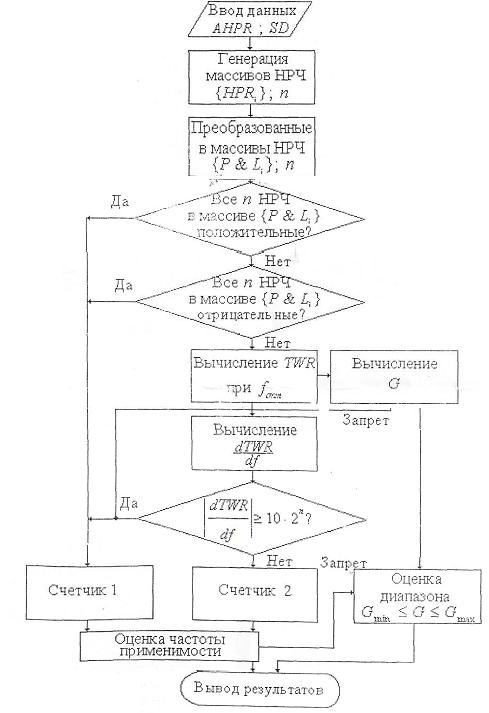
Рисунок 2 - Границы практической применимости «оптимального f» 3. Соотношение (-Р & L) в (4) при нормальном законе распределения случайных величин Р & Li подчиняется закону распределения Коши [2] с бесконечной величиной дисперсии. В конечном итоге эта нормировка, используемая Р. Винсом, приводит к большой величине дисперсии оценок fопт и снижению качества оперативного управления. Таким образом, теория «оптимального f» Р. Винса [1] , по нашему мнению, вызывает серьезные сомнения и подлежит основательной доработке. Применение ее на практике в «чистом виде» затруднительно и требует от инвестора большой осторожности. Результаты имитационного моделированияНами использовалось дискретно-событийное имитационное моделирование, которое широко применяется при решении сложных задач управления экономическими системами [3]. К сожалению, решение подобных задач строгими математическими методами ограничено трудностями вычислительного характера и не всегда приводит к «прозрачности и ясности» полученных результатов. Целью имитационного моделирования является нахождение границ применимости теории «оптимального f» при следующих условиях: - оценки Р & L подчинены нормальному закону; - величины Р & L по модулю не могут превышать 100% из экономических соображений; - доверительная вероятность при оценке границ применимости принята равной 0,9. Имитационное моделирование проводилось в среде MS Exel по блок-схеме эксперимента, изображенной на рис.3.
Рисунок 3 - Блок-схема имитационного эксперимента В качестве входных данных использовались AHPR и SD (1). Далее осуществлялась генерация нормально распределенных чисел (НРЧ) в виде массивов {HPRi} с объемом выборки n. Массивы {HPR}i преобразовывались в массивы {Р & L.} В случае, если в этих массивах все n чисел положительные, то вычисление fопт по (4) невозможно из-за отсутствия Р &Ljmin. В противоположном случае (когда все они отрицательные и G < 1) выражение (4) также не применимо (поскольку реинвестирование принципиально невозможно). Для каждого массива {Р & L} находилось значение TWR и G. Экономические ограничения введены путем измерения величин dTWR/df. Счетчик 1 определял количество массивов {Р & L.}, по которым нельзя, оценить fопт . Счетчик 2 - количество массивов, по которым это удается делать. По показаниям этих счетчиков вычислялась «вероятность успеха». Если она была равна или превышала Рдов = 0,9, то это позволяло оценить. Исследования показали, что при принятых допущениях и ограничениях применять теорию «оптимального f» на практике можно только в определенных границах. Диапазон границ сильно зависит от объема выборки n и величины Pt . При n < 15 и Рдов = 0,9 вообще не целесообразно использовать теорию «оптимального f». С увеличением n границы допустимых значений G расширяются, но они, при принятых выше допущениях и ограничениях, не могут превзойти интервал 1 < G < 1,5 . По мнению авторов, при оперативном управлении капиталом с реинвестированием, если G > 1,5 , недопустимо использовать (1) - (4) из-за непредсказуемого роста инвестиционного риска. В этой ситуации инвестор должен использовать f = fопт , которая оптимальна при G=1,5. Это, естественно,приведет к снижению TWR . При этом, однако, произойдет снижение максимального экономического эффекта от реинвестирования, которое будет оправдано приемлемым инвестиционным риском. Эксперимент показал, что на увеличение нижней границы Gmin, в основном, влияют следующие факторы (n=20):
На уменьшение G (« = 20) влияют:
В случае выборки малого объема (n = 5) на увеличение Gmin влияют:
Аналогично, для G при n = 5 имеем:
Таким образом, невозможность практического использования «оптимального f» по Р. Винсу, в основном, определяется: низкой точностью оценок AHPR ; отсутствием в выборках малого объема {Р &L} проигрышей; «фантастическими значениями TWR» из-за нелинейных эффектов (4) (такие значения TWR не могут быть реализованы в современных экономических системах из-за сильной конкуренции между субъектами предпринимательской деятельности). ВыводыНа основании проведенных исследований можно сформулировать следующие выводы, способствующие снижению вероятности возможного ущерба от применения теории «оптимального f» Р. Винса. Теория «оптимального f» Р. Винса является верной, но слишком академичной и требует осторожного ее использования на практике при реализации инвестиционной политики с реинвестированием. Она нуждается в существенной доработке. В случае практического использования теории «оптимального f» следует учитывать, что границы ее применимости зависят от величины выборки n массива Р & L. и величины доверительной вероятности Р)т. При нормальном законе распределения Р & L , | Р & L |< 100% и лежат в пределах n > 60 эти границы 1 < G < 1,5 с Рдов= 0,9 . Динамическое управление капиталом при реинвестировании с помощью «оптимального f» при допущениях и ограничениях п.2 данных выводов невозможно, если величина выборки Р & L меньше 15 (n<15) из-за существенных инвестиционных рисков. В случае управления экономическими системами с очень высокими показателями (при (n > 1,5) в большинстве практических случаях не целесообразно использовать fопт по Р. Винсу из-за значительных инвестиционных рисков. Следует использовать f = fk , где f соответствует Gmax = 1,5 по Р. Винсу. Результаты данных исследований будут полезны портфельным менеджерам, инвесторам, трейдерам, которые ведут агрессивную инвестиционную политику с реинвестированием своих средств, и будут способствовать получению ними существенных дополнительных прибылей, лежащих над инвестиционными рисками. Литература
|
 – соответственно среднее геометрическое и среднее арифметическое выигрышей (проигрышей) системы;n - количество сделок или отчетных примеров.
– соответственно среднее геометрическое и среднее арифметическое выигрышей (проигрышей) системы;n - количество сделок или отчетных примеров.  (3)
(3)  (4)
(4)