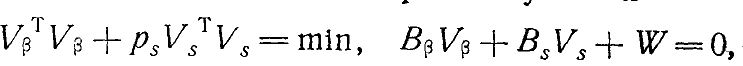Ещё раз о выборе весов при уравнивании линейно-угловых сетей
Автор Ю.И. Маркузе, "Геодезия и картография", 1977, №2, с. 41-43
В работе [1] рассмотрено уравнивание линейно-угловых сетей, когда веса длин сторон точно не известны, и предложена такая его процедура, при которой оптимальными признаются результаты варианта, в котором совпадают принятая до уравнивания и полученная после него ошибки единицы веса, совмещенные со стандартом угловых измерений, полагаемым известным. Такой вариант уравнивания предлагается отыскивать, изменяя среднюю квадратическую ошибку длины стороны через определенные интервалы. В этой же статье автор приводит некоторые оптимальные вероятностные свойства результатов уравнивания.
Поскольку рассмотренный вопрос представляет теоретический и практический интерес, целесообразно остановиться еще раз на некоторых положениях, приведенных в работах [1, 2].
Требование, чтобы принятый до уравнивания стандарт единицы веса c0 = cВ совпал с его оценкой µ, полученной после уравнивания, необоснованно, µ - случайная величина, зависящая от результатов измерений, и ее совпадение с c0 - практически невозможное событие. Это справедливо как при приближенных, так и при точных весах линейных измерений. Поэтому такое требование не содержит правильных предпосылок для определения весов линейных измерений.
Ссылка на работу [3] в оправдание этого требования несостоятельная. В работе [3] на с. 81 написано: "... полное совпадение m' и m вообще может быть только случайным (и потому мало убедительным)". И далее: "Но и обратное, чрезмерно резкое расхождение m' и m покажет вычислителю, что наблюдения, которые он обрабатывает, несомненно отягощены не только одними случайными погрешностями". Конечно, к этому расхождению могут привести также необоснованно установленные веса ps в рассматриваемой задаче. Значит, при условии отсутствия систематических ошибок и ошибок исходных данных можно подобрать ps так, чтобы расхождение между c0 и µ не превысило некоторую величину. Такой величиной может служить длина доверительного интервала, построенного для с0 по результатам уравнивания. Можно сократить этот интервал до отрезка длиной cµ, что рекомендуется в работе [3], но нельзя требовать совпадения с0 и µ.
Но даже приняв условие c0 = µ, следовало бы доказать, что вообще существует решение задачи уравнивания, при котором c0 совпала с µ. При этом мы имеем в виду совпадение этих величин не в пределах точности вычислений, а в математически строгом смысле. Без доказательства этого все выводы работы [1] становятся бесполезными.
Остановимся на этих выводах, напомнив, что в соответствии с обозначениями, принятыми в работе [1], ps - точный вес длины стороны, µ - средняя квадратическая ошибка единицы веса, полученная при точном весе, p's - вес, вычисленный путем подбора ms в варианте, когда средняя квадратическая ошибка единицы веса µ' совпадает с принятым стандартом сВ угловых измерений.
В работе [1] приведена разность
 |
(1) |
и доказывается, что
Доказательство этих положении тривиально и не вызывает возражений. Оно следует из того факта, что
и конечно.
Далее делается попытка доказать, что
Для этого рассматриваются функции
 |
(2) |
 |
(3) |
где l1, l2,...ln - результаты угловых и линейных измерений.
После дифференцирования и замены дифференциалов ошибками (а точнее приращениями) автор получает равенства
 |
(4) |
 |
(5) |
По поводу этих равенств следует заметить следующее. Во-первых, они являются приближенными, а не точными, так как для нелинейных функций, какими являются (2) и (3), приращения Dµ2 и Dµ'2 не равны дифференциалам. Дифференциал dp's следует писать вместо Dp's, так как р's - зависимая переменная. Кроме того, поскольку приращение Dp's заведомо не стремится к нулю, то эти равенства могут быть (в зависимости от вида функции ф) грубо приближенными. Поэтому изучать вероятностные свойства p's на основе равенств (4) и (5) некорректно.
Во-вторых, остается неясным, почему Dµ2 соответствует равенству (1), а Dµ'2 = 0. Эти приращения зависят от того, в какой точке взяты производные функций (2) и (3), и приравнивать их соответственно равенству (1) и нулю, даже если бы эти функции были линейными, совершенно необоснованно. Так что приращения Dµ2 и Dµ'2 не обладают теми свойствами, какие приписывает им автор, и выводы неверны.
По этой причине нельзя считать доказанными выводы автора о том, что значения неизвестных х', у', z'..., определенные по способу наименьших квадратов при приближенном весе р'S, обладают свойством состоятельности. Это противоречит известной теореме о том, что при уравнивании по способу наименьших квадратов измерений с любой невырожденной корреляционной матрицей К', не совпадающей с точной матрицей К, результаты получаются несмещенными [4]. В работе [1] они смещены, что наглядно вскрывает ошибку автора.
Некорректно выполнена в предложенном алгоритме и оценка точности уравненных неизвестных через весовые коэффициенты. Совершенно обойден вопрос об эффективности уравненных неизвестных.
В заключение покажем, что на основе способа наименьших квадратов вообще невозможно получить оценку неизвестного веса.
В самом деле, если поставить матричные условия
где ps- неизвестный вес, и попытаться найти вес совместно с поправками, то применительно к коррелатному уравниванию, составив функцию Лагранжа и определив ее минимум, получим
 |
(6) |
Но равенство (6) возможно лишь при Vs = 0 т.e. при условии, что длины сторон измерены безошибочно. Таким образом, по способу наименьших квадратов в указанной ситуации задача не решается. Для её решения необходима дополнительная информация об измерениях, например, предположение о нормальном законе распределения. В этом случае задачу можно решить на основе принципа максимального правдоподобия [5].
Предположение о нормальном законе распределения позволяет также построить доверительный интервал для сВ2 и исправить вес так, чтобы величина с02 попадала в этот интервал.
Таким образом, способ уравнивания линейно-угловых сетей, рассмотренный в работе [1], остается необоснованным и его нельзя рекомендовать к применению.
Литература:
1. Батраков Ю.Г. К уравниванию линейно-угловых систем на ЭВМ. - "Геодезия и картография", 1970, № 12, с. 20-27.
2. . Батраков Ю.Г. Письмо в редакцию. "Геодезия и картография", 1974, № 10, с. 75-76.
3. Идельсон Н. И. Способ наименьших квадратов и теория математической обработки наблюдений. М., Геодезиздат, 1947, 359 с.
4. Шефе Г. Дисперсионный анализ. М., 1963
5. Kubik К. The estimation of the weights of measured quantities within the method of least squares. Bull. geod. 1970, № 95, p. 21-39.