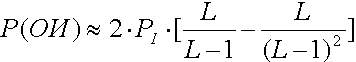Курейчик В.М. Генетические алгоритмы. - Таганрог: изд-во ТРТУ, 1998. - 242 с. // Фундаментальная теорема ГА. стр.65-101.

   Генетический поиск требует наличия популяции хромосом. Будем считать, что популяция хромосом A_j, j=1,2,…,n содержится в популяции A(t) во время (или генерацию) t. Пусть схема H строится из алфавита V={0,1,*}. Так, например, схема H длины 7 следующая:
      H=*11*0** и стринг A=0111000 есть пример реализации этой схемы H.
   Согласно сказанному, схема может быть определена в двоичной хромосоме длины L. Очевидно, что для алфавита мощности k существует (k+1)^L схем, содержащихся в популяции размера n, потому что каждый стринг представляется двумя схемами.
   Все созданные схемы не являются равными. Некоторые более специфичны, чем другие. Например, схема 011*1** имеет больше определенных состояний, чем схема 0******.
   Для количественной оценки схем введены 2 характеристики:
   - порядок схемы - O(H);
   - определенная длина схемы - L(H).
   Порядок схемы - число закрепленных позиций (в двоичном алфавите - число единиц и нулей), представленных в шаблоне. Например, для схемы H=0****** - O(H)=1.
   Определенная длина - есть расстояние между первой и последней числовой стринговой позицией. Например, в схеме H=0011*1** вычислим, L(H)=6-1, а в схеме 0****** вычислим O(H)=1-1=0.
   Предположим, что заданы шаг (временной) t, m примеров схем H, содержащихся в популяции A(t). Все это записывают как m=m(H,t) - возможное различное число разных схем H при заданном t. В процессе репродукции хромосомы копируются согласно их целевой функции или более точно: хромосома Ai получает выбор с вероятностью, определяемой выражением P_i(OP)=f_i(x)/[sumf(x)].
   После сбора непересекающихся популяций размера n с перемещением из популяции A(t) мы ожидаем получить m(H,t+1) представителей схемы H в популяции за время t+1. Это вычисляется уравнением 2.4.

   где f(H) - средняя целевая функция хромосом, представленных схемой H за время t. Если обозначить среднюю целевую функцию всей популяции как f_cр=sum[f(j)]/n, то (2.5)

   Другими словами, частные схемы "растут" как отношение средней целевой функции схемы к средней целевой функции популяции. Схема с ЦФ выше средней в популяции будет получать больше возможности для копирования и наоборот. Правило репродукции Холланда: "схема с ЦФ выше средней живет, копируется, а с ниже средней ЦФ умирает".
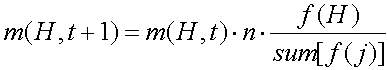
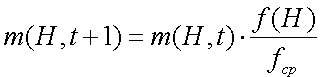
   Предположим, что схема H остается с выше средней ЦФ с величиной c*f_ср, где с-константа. Тогда выражение (2.5) можно модифицировать так (2.6):

   Начиная с t=0 и предполагая, что c - величина постоянная, получим 2.7

   Некоторые исследователи считают, что репродукция может привести к экспоненциальному уменьшению или увеличению схем, особенно если выполнять генерации параллельно.
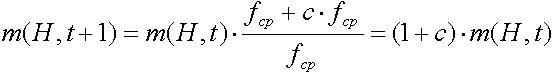
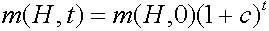
   Лемма 2.1 (Холланд) Если на некотором шаге генерации ГА Р₁ есть вероятность того, что хромосома А определяет потомка на этом шаге и Р₂ есть вероятность, что А уничтожается в течение этого шага, тогда ожидаемое число потомков хромосомы есть Р₁/Р₂.
   Известно также, что вероятность "выживания" хромосомы А на шаге t после ОР определяется величиной (2.8)

   Величина t изменяется от 1,2,…g, где g - число генераций генетического алгоритма.
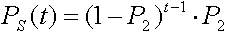
   Отметим, что если мы только копируем старые хромосомы без обмена, поисковое пространство не увеличивается и процесс затухает. Потому и используется ОК (оператор кроссинговера). Он создает новые хромосомы и увеличивает или уменьшает число схем в популяции.
   Рассмотрим, например, частный стринг длины L=7 и две схемы, представляющие этот стринг:
   А = 011|1000,
   H1 = *1*|***0,
   H2 = ***|10**,
    где символ | - символ, обозначающий точку кроссинговера.
   Схема H1 после ОК скорей всего будет уничтожена потому, что 1 в позиции 2 и 0 в позиции 7 расположатся в различных новых стрингах после ОК. Ясно, что схема H2 будет выживать, так как после ОК число 1 в позиции 4 и 0 в позиции 5 будут в том же самом новом стринге. Хотя мы взяли точку ОК случайно, ясно, что схема H1 менее приспособлена к выживанию, чем схема H2. Если точка ОК выбирается случайно среди L-1=7-1=6 возможных позиций, то ясно, что схема H1 уничтожается с вероятностью P(d)=L(H1)/(L-1)=5/6, она же (схема H1) выживает с вероятностью P(s)=1-P(d)=1/6. Аналогичным образом, схема H2 имеет L(H2)=1 и вероятность ее уничтожения P(d)=1/6, а вероятность выживания P(s)=5/6. Очевидно, что нижняя граница вероятности выживания схемы после применения ОК может быть вычислена для любой схемы. Так как схема выживает, когда точка ОК попадает вне "определенной длины", вероятность выживания для простого ОК определяется по формуле 2.9

   Если ОК выполняется посредством случайного выбора, например, с вероятностью Р(ОК), то вероятность выживания схемы определится выражением 2.10

   Очевидно, что выражение (2.10) уменьшается с Р(ОК)=>1.0. Теперь можно асимптотически учесть эффект репродукции и ОК. Снова определим число схем H, ожидаемых в новой генерации. Допуская независимость репродукции и ОК, получим 2.11:

   То есть число схем H в новой генерации зависит от двух факторов:
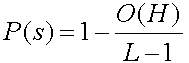
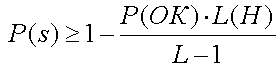
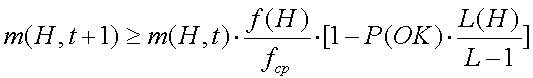
   - ЦФ схемы выше или ниже ЦФ популяции
   - схема имеет "длинную" или "короткую" L(H) (определенную длину).
   Из выражения (2.11) следует, что схемы с выше средней ЦФ и короткой L(H) имеют возможность экспоненциального роста в популяции.
   Рассмотрим влияние мутации на возможности выживания. Напомним, что ОК есть случайная альтернативная перестановка элементов в стринге с вероятностью Р(ОМ). Для того, чтобы схема выжила, все специфические позиции должны выжить. Следовательно единственная хромосома выживает с вероятностью (1-Р(ОМ)) и часто схема выживает, когда каждая из L(H) закрепленных позиций схемы выживает. Умножая вероятность выживания (1-Р(ОМ)) на L(H) получим, что вероятность выживания ОМ (1-Р(ОМ))Р(ОМ). Для малых величин Р(ОМ) (Р(ОМ)<<1) схема вероятности выживания может быть аппроксимирована к выражению 2.12

   Тогда частная схема H получает ожидаемое число копий в следующей генерации после ОР, ОК ОМ, которое определяется по формуле 2.13:

   Это выражение называется "схема теорем" или фундаментальная теорема ГА.
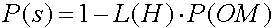
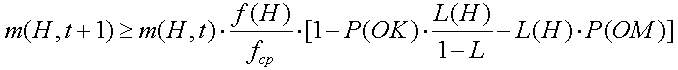
   Вероятность выживания схемы H после применения ОИ (оператора инверсии) можно записать (2.14):

   где L - длина схемы H, а PI - вероятность выбора хромосомы, соответствующей схеме H из популяции на заданном шаге генерации.