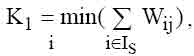Для единичного производства характерна широкая номенклатура изделий при единичных и малых разовых объемах выпуска, вследствие этого также разнообразная номенклатура деталей и операций, выполняемых на рабочих местах. Это порождает нестабильность производственных условий на участках и значительно усложняет организацию и планирование производства [1].
Оперативное планирование начинается с объемного планирования, в рамках которого распределяется номенклатура продукции по цехам, согласно отрезкам планового года. После объемных расчетов разрабатывается календарный план производства, который является расписанием работ по заказу в рамках требуемой продолжительности, т. е. распределение производственных работ по срокам для каждого цеха (участка, оборудования), а также разработка календарных нормативов (межоперационных заделов, порядок запуска деталей в производство). Календарный план должен обеспечить равномерный выпуск продукции в заданные сроки на имеющемся оборудовании, максимально его загрузив.
Календарные расчеты должны определить уровень загрузки оборудования, согласно портфелю заказов. Существующие разработки в области оперативного планирования не позволяют охватить все аспекты производственной деятельности предприятий с единичным типом производства в условиях нестабильной экономической ситуации, когда приостановка производства крупного изделия или, наоборот, появление более выгодного заказа требует немедленной корректировки утвержденных планов [2].
Целью статьи является совершенствование оперативного планирования единичного производства с помощью методов искусственного интеллекта.
Задачи исследования: анализ существующих методов искусственного интеллекта, используемых для оперативного планирования; сравнение методов и выбор наилучшего, позволяющего получить оптимальное расписание производственных работ.
С точки зрения оптимизации, все решения, получаемые в результате выработки планов, можно разделить на следующие: оптимальные по всем критериям; оптимизированные по одному/нескольким критериям; приемлемые по всем ограничениям.
Процесс построения производственного расписания можно разделить на две подзадачи: нахождение возможных расписаний производственных работ на основе различных при оритетных правил и выделение из них наилучшего (оптимального или очень близкого к оптимальному), согласно требуемых критериев.Согласно результатам большинства исследований, детерминированные задачи календарного планирования относятся к NP-трудным задачам упорядочения и носят комбинаторный характер [2]. Выбор оптимального, или "близкого" к оптимальному, расписания осуществляется с помощью одного из четырех подходов: комбинаторного, математического программирования, эвристического и статистического моделирования.
Выбор оптимального расписания заданного набора работ на имеющемся оборудовании исследуется уже давно, но оптимальные решения получены лишь для простейших случаев.
Алгоритмы построения расписаний без проведения полного или частичного перебора вариантов являются решающими эвристическими правилами и играют важную роль в прикладной теории расписаний. Однако эвристические алгоритмы основаны на приеме, который называется "снижением требований". Он заключается в отказе от поиска оптимального решения и нахождения вместо этого "хорошего решения" за приемлемое время. Методы, применяемые для построения алгоритмов такого типа, сильно зависят от специфики задачи [3]. То есть универсального алгоритма не существует и использование того или иного эвристического правила нужно начинать после того, как конкретная производственная задача была решена разными методами и выбрано более подходящее решение, согласно экспертным оценкам с учетом требуемых ограничений и критериев оптимальности.
Научное направление Natural Computing, интенсивно развивающееся в последнее время, основано на принципах природных механизмов принятия решений и включает генетические алгоритмы, нейро-сетевые вычисления, клеточные автоматы, муравьиные алгоритмы, метод роящихся частиц, табуированный поиск и др. [4].
Генетические алгоритмы, используя аналогию между естественным отбором и процессом выбора наилучшего решения из множества возможных, являются одним из самых распространённых вариантов реализации эволюционных алгоритмов. Моделируя отбор лучших планов как процесс эволюции в популяции особей, можно получить решение задачи оптимизации, задав начальные условия эволюционного процесса. В современных условиях локальный поиск на базе генетических алгоритмов реализуется достаточно просто. Преимуществом генетических алгоритмов перед другими является простота их реализации, относительно высокая скорость работы, параллельный поиск решения сразу несколькими особями, позволяющий избежать попадания в "ловушку" локальных оптимумов (нахождения первого попавшегося, но не самого удачного оптимума). Недостаток - сложность выбора схемы кодирования, то есть выбора параметров и вида их кодирования в "хромосомах", возможность вырождения популяции, сложность описания ограничений планирования. В силу этих факторов, генетические алгоритмы нужно рассматривать как инструмент научного исследования, а не средство анализа данных.
Метод роящихся частиц (particle swarm) наиболее простой и один из самых молодых методов эволюционного программирования. Группа исследователей пришла к выводу о возможности решения задач оптимизации с помощью моделирования поведения групп животных. Этот алгоритм благодаря своей простоте (менее десяти строк кода) и скорости считается очень перспективным для задач планирования.
Табуированный поиск (Tabu Search) представляет собой вариацию известного метода градиентного спуска с памятью. В процессе поиска ведётся список табуированных (запре- щённых для перехода) позиций из числа уже рассчитанных. Критическими параметрами алгоритма является диапазон запретов. В процессе поиска осуществляются операции включения в запрещённый список состояний вокруг текущего состояния, что добавляет фактор случайности в процесс поиска [5].
С целью уменьшения времени ожидания обработки для всех деталей или узлов заказа, простоев оборудования, а также сокращения времени всего производственного цикла выполнения заказа решение задачи оптимизации производственного процесса можно выполнять в соответствии со следующими критериями:
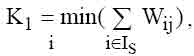где 
- интервал времени между окончанием (j-1)-й и началом j-й операции i -ой детали; 
- множество деталей заказа s. 
где 
- трудоемкость операции i-той детали на k-том станке, 
- длительность прохождения i-той детали в системе, включая время простоя; 
- общая длительность всех операций i-той детали; 
- длительность выполнения операции; 
- множество операций i-той детали. 
, где
- объем работ, который необходимо выполнить по i-той детали заказа s. Сущность оперативно-календарного планирования отражает критерий оптимальности - минимизация длительности выполнения плана или суммарного времени ожидания обслуживания деталей (изделий). Таким образом, поиск оптимального плана - это сведение к минимуму не столько простоя оборудования, сколько времени, в течение которого детали ожидают обработки. Сведение к минимуму времени ожидания обеспечивается расчетом времени обработки всех деталей, при котором наилучшим образом синхронизируется длительность технологических операций и повышается загрузка оборудования. В единичном производстве возникают частые простои оборудования из-за сложности оперативного управления, которое включает построение календарных планов на короткие промежутка времени (неделя, сутки, смена). При разработке планов необходимо учитывать состояния всех элементов производственной системы: работоспособность оборудования, обеспеченность материалами, наличие необходимых инструментов.
Многие реальные производственные задачи формулируются как поиск оптимального значения, где значение - это сложная функция, зависящая от многих входных параметров. Оптимизация многопараметрических функций - наиболее популярное приложение генетических алгоритмов. При формировании расписания некоторые параметры имеют случайный характер, что влияет на ход производства и исполнение плана. Расписание является идеализацией технологического процесса. В реальных условиях возникают отклонения, которые могут быть связаны с поломками оборудования или инструмента, отсутствием сырья на складах, браком какой-либо детали. Возникает необходимость внесения изменений в расписание. Поэтому качество составленного в процессе перепланирования расписания зависит от того, какие данные можно ввести в систему в рамках контроля отклонений и сколько на это потребуется времени. Перепланирование является одним из важных элементов поддержания расписания в актуальном состоянии.
Использование эволюционных методов, например, муравьиного алгоритма, позволяет решить задачу минимизации переналадки и простоев оборудования при большом числе станков [4]. Процесс переналадки занимает важное место в системе планирования, так как он занимает значительную часть общего календарного времени (от нескольких часов до целой смены). Чем чаще требуется переналадка (по условиям производства), тем больше оказываются потери времени. Поэтому одной из основных задач является совершенствование систем переналадки оборудования, а также использование методов, которые позволяют получить оптимальную последовательность обработки деталей на станках с минимальными потерями времени на переналадку.
По сравнению с другими методами данный алгоритм дает наилучшие решения, но требует больше времени на вычисления, чем, например, табуированный поиск, который находит хорошее решение (но не оптимальное) в пять раз быстрее. Использование генетического алгоритма для решения задачи распределения заказов по станкам и равномерной их загрузки позволяет получить решение, почти такое же, как и муравьиный алгоритм. При этом время поиска решения на 15% меньше, результат отличается не более чем на 2%. При малых объемах задачи дают одинаковые результаты [4] Сравнивая муравьиный алгоритм с точными методами, например динамическим программированием или методом ветвей и границ, можно сказать, что он находит близкие к оптимальному решения за значительно меньшее время даже для задач небольшой размерности. Вышеописанные алгоритмы оптимизации для составления детальных производствен- ных расписаний относятся к классу APS-систем (Advanced Planning & Scheduling), относительно молодому направлению корпоративных информационных систем. Являясь инструментами имитационного моделирования производственной деятельности, APS-системы применяются для поддержки принятия решений при оперативном управлении предприятием [5].
Для исключения недостатков подобных разработок необходимо использовать эволюционные методы, которые позволили бы получать оптимальные решения проблем реальных производственных ситуаций за малое время. При решении такие методы рассматривают систему планирования как чёрный ящик, когда на входе задаются различные значения параметров планирования, после чего оценивается эффективность получаемых расписаний с точки зрения ключевых показателей эффективности.
На основе анализа существующих разработок в области эволюционных методов перспективным решением сложных комбинаторных задач оптимизации является гибридное использование генетического и муравьиного алгоритмов. Это позволит существенно улучшить систему оперативного планирования, тем самым сократив время получения оптимальных или приемлемых производственных расписаний. Также при появлении случайных событий, влияющих на процесс производства, позволит быстро реагировать на изменение и внесение корректив в исходные данные. Для развития систем планирования возможна разработка программного продукта, позволяющего строить оптимальные производственные планы, используя инструменты эволюционных методов.