"Введение в генетические алгоритмы для ученых и инженеров"
Дэвид А. Колей
Глава 4, 59-67стр.

4.1 Передовые операторы.

   Хотя простой генетический алгоритм, такой как ЛГА, может быть использован для решения некоторых проблем, существуют многочисленные расширения алгоритма, которые были развиты, чтобы помочь улучшить выполнеие и расширить область применения. Они включают более эффективные кроссинговер и алгоритмы селекции, алгоритмы, которые преднамеренно ищут локальные оптимумы, методы комбинаторной оптимизации, методы, имеющие дело с мультикритериальными проблемами и гибридные алгоритмы, объединяющие скорость традиционных методов поиска с надежностью ГА. Будучи вводным текстом, многие из этих расширений не даны в полном объеме и только подчеркнуты. Для дополнительных деталей читатель направлен на другие тексты в специальных ссылках [MI94, ZA97 и BA96]. Кроме того, некоторые из методов описаны более детально и затем применены в различных проблемах в главе 6.

Комбинаторная оптимизация.

   Много проблем не требуют оптимизации серии реально-оцененных параметров, но открытия идеально отсортированного списка, классический пример чего - задача коммивояжера (ЗК). В ЗК фиктивный продавец предполагает необходимость нахождения самого короткого маршрута между серией городов. Типично правила устанавливают, что ни один город не может быть посещен более одного раза. Другие примеры таких комбинаторных проблем – размещение газовых и водных труб, структурный проект, планирование цеха и расписание.

   Большое усилие было применено к попытке найти эффективные алгоритмы для решения таких проблем и эта работа была продолжена с введением ГА. Главная проблема в применении генетических алгоритмов, описанных до сих пор, это, что кроссинговер и мутация имеют потенциал для создания невыполнимых туров. Чтобы увидеть это рассмотрим задачу коммивояжера, описанную на рисунке 4.1. Здесь восемь городов, помеченных от a до h, размещенных случайным образом.

Рисунок 4.1 Задача коммивояжера. Какой самый короткий маршрут, объединяющий все восемь городов?

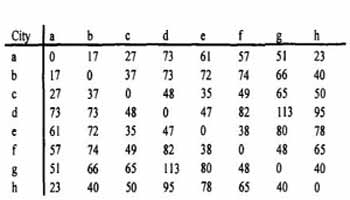
Таблица 4.1 Расстояния в км между городами на рис 4.1.

   Один пример тура может быть b c de ghfa, другой – c b gf adeh. Если одноточечный кроссинговер применить к этим турам, то результат разреза по средней точке такой bcdeadef и cbgfghfa. Ниодно из этих представлений не является завершенным туром.

   Так как оператор кроссинговера должен быть построен, чтобы генерировать только полные туры? Если строка, используемая для представленя туров, остается фиксированной длины, тогда это также подразумевает, что каждый город может быть посещен однажды. Существует много способов конструирования такого оператора. Один – применить вначале кроссинговер, а потом отклонить сгенерированные неполные туры. Тем не менее, это требует отклонения большинства туров и относительно легко представить менее раточительные алгоритмы. Одна возможность – частично подобранный кроссинговер (ЧПК).

   Представление ЗК, описанное выше, дает строки с различными свойствами в строке учета реально-оцененной оптимизации проблемы. Позиция и значение элемента взаимосвязаны. Фактически, в пределах задачи коммивояжера только порядок имеет значение. Идеально, если новые операторы кроссинговера и мутации должны создавать не только выполнимые туры, но и иметь возможность объединять строительные блоки родителей с выше среднего пригодностью для произведения более пригодных туров.

   ЧПК происходит простым способом: как и ранее, отбираются родители; случайным образом выбираются две точки кроссинговера (определяющие выбранную секцию); затем операторы обмена применяются для построения двух новых потомственных строк.

   Вернемся к предварительно опеределенным турам и выберем случайно две точки пересечения: Тур 1 = b c | d e g | h f a и Тур 2 = c b | g f a | d e h. Вначале целая центральная часть и выбранная секция обменивается: Тур 1’ = b c | g f a | h f a и Тур 2’ = c b | d e g | d e h.

   Ни один из этих туров не является выполнимым. В туре 1’ отсутствуют города d и e, в туре 2’ города a и f не посещены. Так как строки имеют фиксированную длину, это значит, что оба тура посещают некоторые города более одного раза. В случае тура 1’ города а и f посещены дважды, тур 2’ посещает дважды d и e. По определению, одно из этих повторений в пределах выбранной секции и одно вне.Также по определению, любой город, который посещен дважды одним туром, должен отсутствовать в другом туре. Это предлагает путь вперед. Города, которые посещены дважды в одном туре, меняются с городами, которые посещены дважды в другом туре. Только один представитель (вне выбранной секции) из таких городов меняется, иначе процесс будет циклическим и неконструктивным. Так, в примере, город а вне выбранной секции тура 1’ меняется с d тура 2’, и аналогично города f и e. Два тура: тур 1’’ = bcgfahed и тур 2’’ = cbdegafh сформированы, каждый из которых полон.

   ЧПК относительно легко осуществить в пределах ЛГА, делая подходящие изменения в операторе кроссинговера и устанавливая Рм в ноль.

4.2 Расположение альтернативных решений, используя ниши и разновидности.

   В большинстве проблем оптимизации ведется поиск лучшего решения. Это может быть глобальный оптимум, если он может быть найден, или точка в окрестности глобального оптимума, если задача очень большая и сложная. Тем не менее некоторые проблемы характеризуются поиском ряда вариантов вместо уникального вектора решения. Проблемы, в которых эти варианты расположены на некотором расстоянии от глобального оптимума, особенно интересны. В таких случаях существует вероятность, что варианты отделены областями, которые приравнивают к наиболее скудным решениям; вместо того, чтобы пытаться избежать локальных оптимумов, идея – пытаться охотиться на них. Такой ландшафт пригодности иллюстрируется мультимодальной функцией f(x) и показан на рисунке 4.2. Хотя интуитивно здесь есть что-то отличительное в значениях х, которые приравниваются к пикам f(x), математически ни один из них не дает роста пригодности более, чем большинство точек рядом с глобальным оптимумом. Это уклоняется от предмета спора, почему охотяться на определенно такие значения х, если любая точка рядом с глобальным оптимумом вероятно произведет болем высокую пригодность так или иначе?

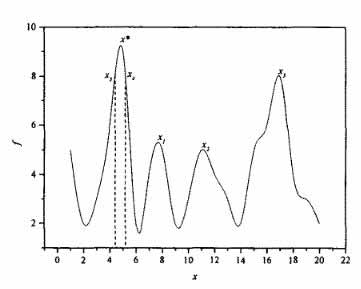
Рисунок 4.2. Мультимодальная функция с глобальным оптимумов в x* и локальными оптимумами в x1, x2 и x3.

   Одна причина для попыток таких поисков может быть объяснена на примере. Если проблема, характеризуемая ландшафтом пригодности на рисунке 4.2, была бы архитектурной, в которой х – угол наклона крыши и f – инверсия финансовой стоимости строительства, тогда каждый локальный оптимум имел бы существенное значение. Они представляют хорошие, но не идеальные, финансовые решения радикально разной формы. Если стоимость – единственный критерий, то угол х* - единый выбор; однако, если любое из решений x1, x2 или x3 считались бы более соответствующими визуальному желанию, то архитектор мог бы убедить клиента в необходимости инвестировать небольшое количество дополнительного капитала. Хотя существует много точек близких к глобальному оптимуму, которые предлагают лучшие значения f, чем любой локальный оптимум, их близость к глобальному оптимуму может произвести небольшое оправдание за то, чтобы принять этот проект, а не оптимум. Это не так для тех структур, которые представлены локальными оптимумами. В основном, оптимизация используется как фильтр, фильтр отвечает задаче по поиску высокого выполнения, новых решений проблемы поперек целому пространству проблемы и игнорирует, на сколько это возможно, все остальные точки. Один способ нахождения таких оптимумов – просто использование многократных пробегов.

   На рисунке 4.3 показано более сложное пространство поиска. Поиск предусматривает нахождение метода, который может эффективно от фильтровать любе точки, которые генерируют пригодность, меньшую, чем некоторый минимум fmin. Такой фильтр в идеале генерирует фигуру 4.4, которую легче интерпретировать, чем оригинальную функцию. На рисунке показано, что фильтрование легко применять вручную, так как значение f известно в любой точке (x,y) в пределах пространства проблемы. Обычно f вероятно слишком сложна для оценивания, чем маленькая фракция в пространстве поиска. Поэтому необходим метод, который сможет охотиться на пики в пределах сложного ландшафта. Это несколько нелепо; досих пор центральным рассмотрением было предотвращение локальных оптимумов, сейчас имеет место желание активно искать их.

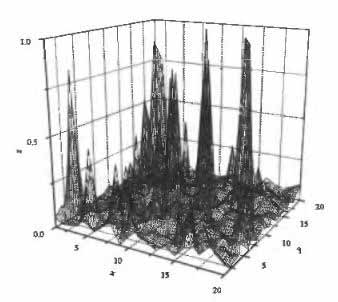
Рисунок 4.3. Более сложный многопиковый ландщафт; точки интереса те, в которых f>fmin

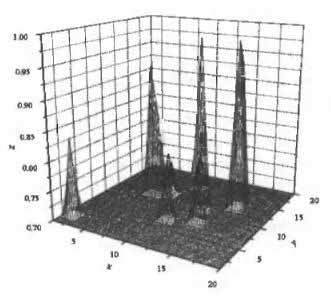
Рисунок 4.4. Фильтр для фигуры на рисунке 4.3 показывает только точки, в которых f>fmin

   В природе исследование отдельных фракций в пространстве поиска (или ниши) подмножествами популяции (или разновидностями) происходит с готовностью. В применении этого к ГА, две саме важне концепции оказываются разделение пригодности и ограничения на то, кто с кем будет скрещиваться. Это скрещивание должно быть ограничено близостью строк, что в целом неудивительно, это после всех одно из определений разновидности. Разделение пригодности между строками важно и более интересно.

© Ю. Н. Логвинова, ДонНТУ,2008г.