Источник: Герасимяк Р.П., Лещёв В.П. Анализ и синтез крановых электромеханических систем. – Одесса, СМИЛ, 2008. – с. 144-149
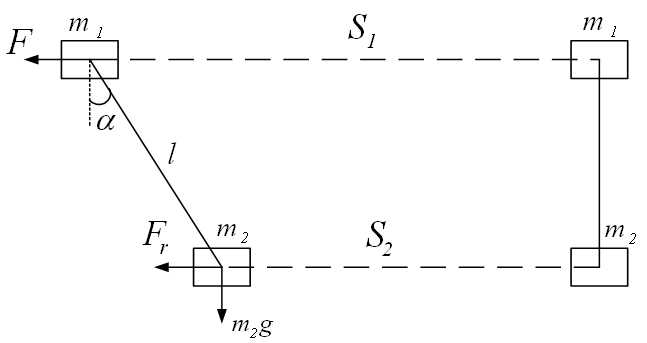
К подобным механизмам отнесём механизмы пере¬мещения моста и тележки мостового крана, а также козлового крана и мостовых перегружателей. Для анализа работы исследуемой механической части ЭМС рассмотрим процесс пуска механизма передвижения грузоподъемной тележки с подвешенным на гибкой нити (канате) грузом, описав его дифференциальными уравнениями. Известна расчетная схема механической части для этого случая [3,4], изображенная на рис. 4.1.На этом этапе исследования механизм представлен в виде двух поступательно движущихся масс: m1 – тележки (моста) и m2 – груза, подвешенного на гибкой нити длиной l, s1 и s2 – пути их перемещения соответственно.
Пуск происходит под действием приложенного непосредственно к тележке динамического усилия
F, представляющего собой разность усилия (момента), создаваемого двигателем, и силы статического
сопротивления (силы трения). Если известно значение силы сопротивления, то величина F определяет усилие
(момент) двигателя. Здесь удобно все величины приводить к поступательному движению тележки, так как нас интересует
поведение подвешенного груза и реальный угол его отклонения от вертикали 
. Полагаем, что до начала разгона люфты в передачах выбраны, а нить нерастяжима, т.е. длина l
не зависит от веса груза. Кроме того, все выкладки этой главы производятся без учёта возможных дополнительных
внешних воздействий – влияния ветровой нагрузки и пр.
Пренебрегая потерями при деформации нити, движение рассматриваемой системы можно описать известными дифференциальными уравнениями [4]:
(4.1)
(4.2)где горизонтальная составляющая от силы веса груза m2g, эквивалентная усилию упругой линейной деформации,
(4.3)В последнем выражении величина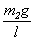 
адекватна коэффициенту жесткости C12 при линейной деформации, g – ускорение
свободного падения.
Отклонение груза от вертикали характеризуется углом . При реальных малых углах отклонения (5-10 град.) с достаточно высокой степенью
точности можно считать sin=
, тогда
и, следовательно,
(4.4)Преобразуя уравнения (4.1) и (4.2), с учетом формулы (4.4) получаем выражение, связывающее угол отклонения груза с задающим воздействием,
(4.5)где частота собственных колебаний системы "тележка - груз"
(4.6)a 
0 – известная частота
колебаний математического маятника, подвешенного на конструкции с бесконечной массой (
),
(4.7)Здесь и далее коэффициенты соотношения масс (1.48), (3.10)
, Перейдя к операторной форме записи уравнения (4.5), с учетом (4.6) получаем
передаточную функцию для угла
(4.8)Решение уравнения, записанного по передаточной функции (4.8), при нулевых начальных условиях и действии постоянной силы F (например, при пуске) приводит к зависимости
(4.9)графически изображённой на рис. 4.2 и отображающей незатухающие колебания, которые груз совершает с частотой
относительно наклонной оси, а угол
меняется от 0 до
Решение однородного дифференциального уравнения, соответствующего (4.5), после достижения
скорости тележки 
заданного значения
V1зад и F=0 и потому при ненулевых начальных условиях принимает вид:
(4.10)где н и
'н – начальные значения
угла и его производной, являющиеся конечными для режима, описываемого зависимостью (4.9).
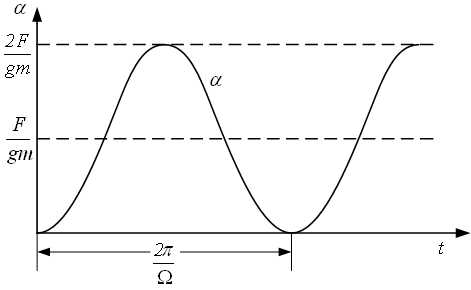
Если переходный процесс пуска заканчивается точно через промежуток времени
Если переходный процесс пуска заканчивается точно через промежуток времени
, где n= 1,2,3,...
(рис. 4.2), то груз после прекращения действия силы больше не колеблется (F=0;
=0). Однако если время переходного
процесса отлично от значений ,
колебания сохраняются, а их амплитуда зависит от начальных условий.
Таким образом, амплитуда колебаний в соответствии с формулой (4.9) пропорциональна усилию F, а следовательно, и динамическому моменту двигателя и при его уменьшении также снижается. Однако снижать момент двигателя для ограничения амплитуды раскачивания – это значит увеличивать время переходных процессов, что ведет, естественно, к снижению производительности механизма.
Предложено много различных способов демпфирования колебаний подвешенного на канате груза
[1, 3, 4, 5]. Здесь мы остановимся на способе, который оптимизирует переходные процессы и потому обеспечивает
их максимальное быстродействие. Следовательно, необходимо найти такой закон изменения усилия F, который
обеспечивал бы минимальное время переходного процесса с учетом требований, предъявляемых дополнительно, а именно:
к концу разгона или торможения, которые протекают за минимальное время, нить с грузом должна располагаться
вертикально, т.е. угол отклонения её от вертикали =0 (рис.4.1) [2]. При этом предполагается, что используется такой регулируемый асинхронный электропривод,
который может обеспечить любой требуемый закон изменения динамического момента (усилия F).