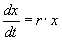 ,(1.1)
,(1.1)
где x – численность (плотность) популяции, t – время, r – мальтузианский параметр, имеющий смысл удельной скорости роста. Размерность мальтузианского параметра – [время-1]. Решением данного уравнения является выражение:
Теория: Нелимитированный рост численности популяции при постоянных условиях среды описывается дифференциальным уравнением Мальтуса (Ризниченко, Рубин, 1993) :
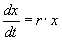 ,(1.1)
,(1.1)
где x – численность (плотность) популяции, t – время, r – мальтузианский параметр, имеющий смысл удельной скорости роста. Размерность мальтузианского параметра – [время-1]. Решением данного уравнения является выражение:
![]() ,(1.2)
,(1.2)
Задача 1.1
Условия:С целью изучения динамики эвтрификации водоемов, загрязненных минеральными удобрениями, в пяти прудах моделировали размножение синезеленых водорослей в нелимитированных условиях. Полученые данные об изменении численности популяции водорослей в каждом пруду представлены в таблице 1.1.
Таблица 1.1
|
Время, час
t |
Титр клеток водорослей, кл./мл | ||||
| Пруд 1 x1 |
Пруд 2 x2 |
Пруд 3 x3 |
Пруд 4 x4 |
Пруд 5 x5 |
|
| 0 | 135 | 171 | 60 | 252 | 106 |
| 24 | 245 | 270 | 113 | 371 | 201 |
| 48 | 374 | 491 | 186 | 710 | 275 |
| 72 | 545 | 693 | 269 | 1088 | 451 |
| 96 | 839 | 1163 | 447 | 1772 | 689 |
| 120 | 1544 | 1788 | 796 | 2534 | 1304 |
| 144 | 2392 | 3460 | 1024 | 4842 | 2161 |
| 168 | 3433 | 4704 | 2131 | 6478 | 3386 |
| 192 | 6586 | 8526 | 3107 | 10429 | 5326 |
| 216 | 10129 | 13198 | 4351 | 19953 | 8928 |
Вопросы: На основе этих данных определить для популяции водорослей в каждом пруду значение мальтузианского параметра r (удельной скорости размножения) и период удвоения T. Найти также соответствующие медианы по полученным выборкам r и T.
Решение: Нелимитированный рост численности популяции описывается экспоненциальной функцией Мальтуса:
![]() , (1.3)
, (1.3)
где x0 – начальная численность популяции, r – мальтузианский параметр, t – время (см. рис.1.1).
Рис.1.1. Экспоненциальная зависимость численности популяции от времени при условии нелимитированного роста
Таблица 1.2
Рис.1.2. Линеаризация экспоненциальной зависимости, представленной на рис.1.1, и определение мальтузианского параметра r .
Таблица 1.3
T, час Медиану определяем обычным способом как срединное значение в выборке: Ме(r)= 0.0198 час-1, Ме(T)= 35 час. Тема 2. Плотностно-зависимый рост популяций. Логистическое уравнение Ферхюльста.
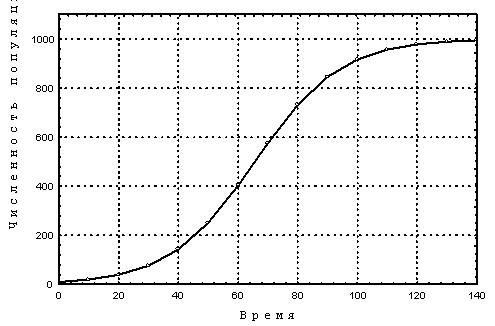
Теория: При ограничении процессов размножения организмов в популяции каким либо ресурсом, например количеством доступной пищи, удельная скорость роста популяции зависит от ее численности (плотности). Математические модели, учитывающие данный эффект, называются моделями плотностно-зависимого роста. Логистическое уравнение Ферхюльста является простейшей моделью из этого ряда. В данной модели предполагается, что удельная скорость роста популяции линейно уменьшается с ростом численности, и имеется также некая предельная численность популяции, K, при достижении которой добавление к популяции новых особей возможно лишь при условии определенной гибели уже имеющихся особей. Эта предельная численность K носит название емкость среды. Данный параметр известен также как ресурсный. Уравнение Ферхюльста имеет следующий вид: Здесь r– мальтузианский параметр, K – ресурсный параметр. Уравнение Ферхюльста имеет аналитическое решение: где x0– начальная численность популяции. Пример логистической популяционной динамики приведен на рис. 2.1 Рис.2.1. Логистический рост популяции. r = 0.07 год-1, K = 1000 особей, >x0 = 10 особей. Условия: В 1937 г. на остров Протекшен у побережья штата Вашингтон завезли двух самцов и шесть самок обыкновенного фазана (Phasianus colchicus). За пять лет численность популяции фазана достигла 1325 размножающихся особей, т.е. возросла в 166 раз. Судя по некоторым признакам, рост этой популяции происходит по логистической кривой. От двух самцов и шести самок, привезенных на остров в 1937 г., она возросла до 30 особей к весне 1938 г., до 81 – в 1939 г., до 282 – в 1940 г., 641 – в 1941 г., 1194 – в 1942 г. и до 1898 – в 1943 г., когда на остров прибыли военные части, и солдаты начали охотиться на фазанов (рис.2.2). Однако, создается впечатление, что к 1943 г. численность популяции фазанов начитает стабилизироваться (Солбриг,Солбриг, 1982).
Рис.2.2. Измнение численности популяции фазанов на острове Протекшен. Вопросы:

Для обработки экспериментальных данных используем логарифмическую форму этого уравнения: (1.4)
(1.4)
С этой целью каждый элемент 2-6 столбцов необходимо разделить на соответствующий начальный элемент и взять натуральный логарифм этого отношения (см. таблицу 1.2).
Далее, для каждого пруда на основе таблицы 1.2 следует построить график, где по оси абсциcc откладывается время, а по оси ординат – соответствующее значение ln (xt/x0), как это показано на рис.1.2. Экспериментальные данные должны сгруппироваться около прямой линии, тангенс угла которой и есть искомое значение мальтузианского параметра r .
Время, час
ln (x1t/x10)
ln (x2t/x20)
ln (x3t/x30)
ln (x4t/x40)
ln (x5t/x50)
0,00
0,00
0,00
0,00
0,00
0,00
24,00
0,60
0,46
0,63
0,39
0,64
48,00
1,02
1,06
1,13
1,04
0,95
72,00
1,40
1,40
1,50
1,46
1,45
96,00
1,83
1,92
2,01
1,95
1,87
120,00
2,44
2,35
2,59
2,31
2,51
144,00
2,87
3,01
2,84
2,96
3,01
168,00
3,24
3,31
3,57
3,25
3,46
192,00
3,89
3,91
3,95
3,72
3,92
216,00
4,32
4,35
4,28
4,37
4,43

Значение периода удвоения T находим по формуле:
 (1.5)
(1.5)
Результаты обработки данных в этой задаче представлены в таблице 1.3.
Пруд 1
Пруд 2
Пруд 3
Пруд 4
Пруд 5
r , час-1
0.0197
0.0201
0.0198
0.0198
0.0204
35.19
34.48
35
35
33.98
 . (2.1)
. (2.1)
 , (2.2)
, (2.2)
Задача 2.1.
Решение:
1. Для ответа на первый вопрос представим данные в координатах {ln(x), t}, где x – численность популяции, t – время. При плотностно-зависимом росте данные в указанных координатах должны отклонятся от прямой линии с течением времени, что и наблюдается в нашем случае (рис.2.3). Это свидетельствует о том, что удельная скорость роста уменьшается с увеличением численности.
 (2.3)
(2.3)
где  и
и  .
.

Рис.2.3. Изменение численности популяции фазанов в полулогарифмических координатах
Для этого на основе первичных данных рассчитаем дополнительные переменные  и
и ![]() , как это указано в таблице 2.1, и представим их в виде графика, где по оси абсцисс будем откладывать
, как это указано в таблице 2.1, и представим их в виде графика, где по оси абсцисс будем откладывать ![]() , а по оси ординат -
, а по оси ординат -  (рис.2.4).
(рис.2.4).
Таблица 2.1
|
Время t |
Численность x |
ln (x) |
|
|
|
| 1937,00 | 8,00 | 2,08 | 19,00 | 1,16 | -5,74 |
| 1938,00 | 30,00 | 3,40 | 55,50 | 0,92 | -4,41 |
| 1939,00 | 81,00 | 4,39 | 181,50 | 1,11 | -3,40 |
| 1940,00 | 282,00 | 5,64 | 461,50 | 0,78 | -2,06 |
| 1941,00 | 641,00 | 6,46 | 917,50 | 0,60 | -1,06 |
| 1942,00 | 1194,00 | 7,09 | 1546,00 | 0,46 | -0,09 |
| 1943,00 | 1898,00 | 7,55 | 1,15 |

Рис.2.4. Определение параметра K по дополнительным переменным, представленным в таб. 2.1.
Точки на графике группируются около прямой линии, которая согласно выражению (2.3) пересекает ось абсцисс в точке, соответствующей величине K (рис.2.4). В рассматриваемом случае величина параметра K равна 2500.

Рис. 2.5. Определение параметра r по данным из таблицы 2.1.
Для нахождения параметра r воспользуемся интегральной формой уравнения Ферхюльста в логарифмическом виде:
 (2.4)
(2.4)
На основе ряда x рассчитаем дополнительную переменную Задача 2.2
Условия: В Кузнецком Алатау на одном из охотучастков велась добыча соболя. Через некоторое время охотоведы заметили резкое снижение численности популяции. Когда численность соболя на участке упала ниже известной критической величины, был сделан вывод о неконтролируемом браконьерском промысле. Контролируемый промысел был остановлен, и был организован ежегодный учет численности популяции соболя. Данные представлены в таблице 2.2 и на рис.2.6. Таблица 2.2 , как указано в таблице 2.1. и построим график для этой переменной против переменной t (рис. 2.5). Как видно, экспериментальные точки группируются около прямой линии, тангенс угла которой согласно выражению (2.4) дает значение параметра r. Для рассматриваемого случая tg a = 1.13. Учитывая размерность шкал получаем искомый ответ: r = 1.13 год-1 .
, как указано в таблице 2.1. и построим график для этой переменной против переменной t (рис. 2.5). Как видно, экспериментальные точки группируются около прямой линии, тангенс угла которой согласно выражению (2.4) дает значение параметра r. Для рассматриваемого случая tg a = 1.13. Учитывая размерность шкал получаем искомый ответ: r = 1.13 год-1 .
Время, год
Численность
Время, год
Численность
0
1120
8
1940
1
1147
9
2072
2
1189
10
2173
3
1253
11
2245
4
1346
12
2293
5
1470
13
2324
6
1620
14
2343
7
1784
15
2355

Рис.2.6. Изменение численности популяции соболя после отмены контролируемого промысла
Вопросы: По данным, представленным в таблице 2.2. определите, сколько соболей в год браконьеры добывали на данном участке Np, каковы кинетические параметры популяции соболей на данном участке (r и K), какова критическая численность популяции в условиях браконьерства xкр. и какова критическая величина промысла Nкр.
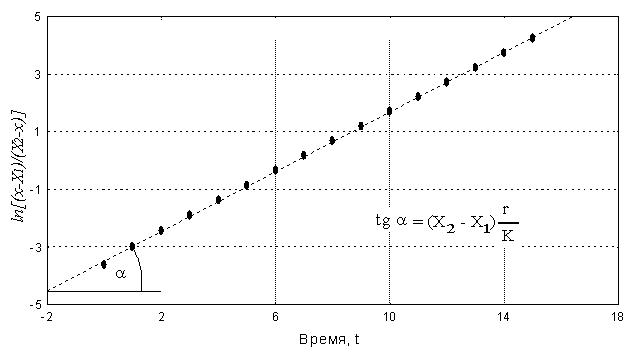
Решение: Будем описывать динамику этой популяции следующим уравнением (Базыкин, 1985): Здесь r - мальтузианский параметр, K – ресурсный параметр, Np – браконьерский промысел. Для решения на первом этапе используем приближенную форму данного уравнения: где С этой целью на основе данных о xi и ti рассчитаем дополнительные переменные Для исследуемой популяции по графику (рис.2.7) определяем, что X1 = 1086 и X2 = 2373. Из этих данных далее определяем значение параметра K, т.к. из теории (Базыкин, 1985) известно, что K = X1 + X2. В нашем случае K =1086 + 2373 = 3459 особей. Знание параметра K и значений X1 и X2 позволяет нам использовать для дальнейшего решения задачи интегральную форму уравнения (2.5): Таблица 2.3 t x Рис.2.7. Определение параметров X1 и X2, по данным из таблицы 2.3. Рассчитаем соответствующую дополнительную переменную Рис.2.8. Определение параметра r по данным из таблицы 2.3.
Для этого графика tg a = 0.517. Далее определяем значение параметра r : Учитывая размерность осей получаем r = 1.39 год-1.
Значение параметра Np (интенсивность браконьерского промысла) находим из выражения: откуда Критическая численность популяции в условиях браконьерского промысла, согласно теории, равна стационарному решению X1, поэтому xкр. = 1086 особей. Критическую величину промысла Nкр находим из соотношения Тема 3. Влияние концентрации лимитирующего субстрата на скорость размножения. Уравнение Моно. Теория: Из множества необходимых для жизнедеятельности пищевых компонентов, субстратов, потребляемых организмами исследуемой популяции, субстрат, находящийся в наименьшей доступности и лимитирующий ростовые процессы, определяет скорость размножения. Этот принцип известен как принцип минимума Либиха. Количественная зависимость удельной скорости размножения r от количества (концентрации) лимитирующего субстрата S, как правило, имеет насыщающий характер и обычно описывается уравнением Моно (Печуркин, 1978; Ризниченко, Рубин, 1993):
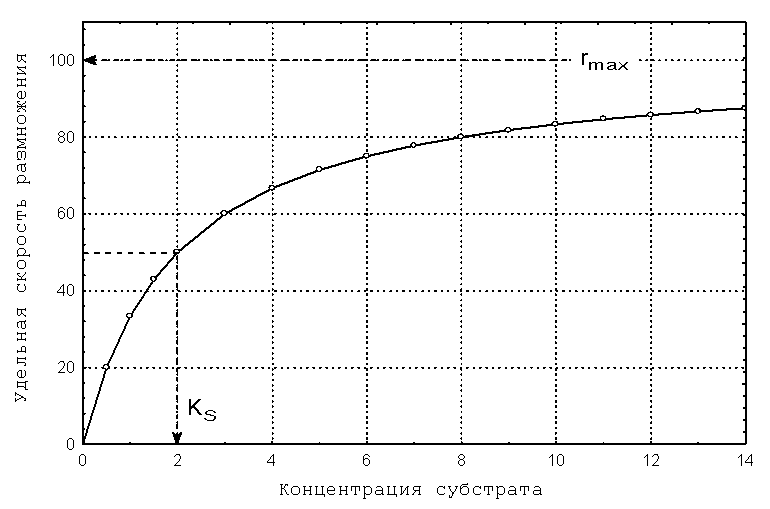
Уравнение Моно имеет два параметра: rmax – максимально возможная скорость размножения при избытке субстрата (размерность – [время]-1) и KS – коэффициент насыщения (размерность – аналогичная размерности субстрата). Согласно теории коэффициент насыщения численно равен той концентрации субстрата, при которой наблюдается половинная от максимальной скорость размножения. Типичный вид зависимости Моно представлен на рис.3.1.
Рис.3.1. Зависимость удельной скорости размножения от концентрации лимитирующего субстрата в соответствии с уравнением Моно Задача 3.1
Условия: С целью определения кинетики размножения популяции бактерий Escherichia coli (кишечная палочка) изучали рост и размножение клеток данных бактерий при различных концентрациях лимитирующего субстрата, глицерина. Клетки выращивали при оптимальных условиях и через каждые полчаса измеряли оптическую плотность культуры (показатель, отражающий численность популяции). Полученные в результате эксперимента данные представлены в таблице 3.1. и на рис.3.2.
Таблица 3.1.
час S100 – концентрация субстрата 100 мг/л и т.д. Вопросы: Определить на основе представленных экспериментальных данных кинетические параметры размножения клеток кишечной палочки (параметры уравнения Моно, rmax и KS)
Решение: На первом этапе обработки экспериментальных данных определим удельную скорость роста r клеток кишечной палочки для каждой концентрации лимитирующего субстрата по алгоритму, рассмотренному в задаче 1.1. В качестве показателя, отражающего относительное изменение численности популяции во времени, будем использовать отношение соответствующих значений оптической плотности Ext /Ex0 (Перт,1978). Рассчитаем для каждой концентрации дополнительную переменную ln(Ext /Ex0) и построим график зависимости этой переменной от времени (таб.3.1. и рис.3.3). Экспериментальные точки для каждой концентрации должны сгруппироваться около соответствующей прямой линии, тангенс угла которой равен оценке r для этой концентрации.
Рис.3.3. Определение значений удельной скорости размножения r клеток E.coli для каждой концентрации лимитирующего субстрата. Обозначения те же, что и на рис.3.2. Определенные таким образом значения r для каждой концентрации лимитирующего субстрата S представлены в таблице 3.2., а соответствующий график – на рис.3.4. Таблица 3.2. Рис.3.4. Зависимость удельной скорости размножения исследуемой популяции кишечной палочки от концентрации лимитирущего субстрата, глицерина Нетрудно видеть, что зависимость удельной скорости размножения от концентрации субстрата для исследуемой популяции имеет вид кривой с насыщением и по всей видимости описывается уравнением Моно (3.1). Для нахождения параметров уравнения Моно воспользуемся методом Корниша-Боудена, “прямым линейным графиком”, разработанным специально для подобного рода зависимостей (Корниш-Боуден, 1979). С этой целью для каждой пары {S, r} из таб.3.2 на оси абсцисс влево будем откладывать значение –S, а на оси ординат – значение r. Далее через точки {-S, 0} и {0, r} проводим прямую линию (рис.3.5), Таких линий на графике будет пять, по числу пар {S, r}. Данные прямые по теории Корниша-Боудена должны пересечься в одной точке, координаты которой дают искомые значения параметров уравнения Моно, KS и rmax. В рассматриваемой задаче из-за наличия ошибок измерений точек пересечения прямых на графике (рис.3.5) больше, около десяти. В этом случае в качестве оценки рекомендуют брать медиану.
Рис.3.5. Определение кинетических параметров размножения клеток кишечной палочки KS и rmax методом Корниша-Боудена на основе данных из таб.3.2. Таким образом, по графику на рис.3.5. определяем, что для исследуемой популяции E.coli кинетические параметры размножения имеют следующие значения:
KS = 48 мг/л, rmax = 0.83 час-1.
Задача 3.2
Условия: Изучали кинетику размножения богомола. Исходя из предположения о пропорциональности между интенсивностью поедания пищи и скоростью размножения, измеряли зависимость между плотностью распределения пищи (мух) и количеством пищи, съеденной в единицу времени одной особью. Данные представлены в таблице 3.3 и на рис.3.6. Таблица 3.3. Рис.3.6. Зависимость между плотностью распределения пищи и количеством пищи, съеденной в единицу времени, для популяции богомола Вопросы: Определить по представленным данным кинетические параметры интенсивности поедания пищи богомолом, а также плотность распределения пищи, мух, при которой скорость размножения популяции богомола будет равна половине от максимальной. Решение: Для ответа на первый вопрос отметим, что судя по графику на рис.3.6. кинетика поедания пищи богомолом подчиняется уравнению типа уравнения Моно: Искомые параметры уравнения Моно Imax и KS определим с помощью метода Корниша-Боудена, как это описано в задаче 3.1., используя данные из таб.3.3. Соответствующее решение предсталено на рис. 3.7.
Таким образом, для кинетики поедания мух богомолом Imax = 28.5 усл.ед., KS = 0.0038 мух/м2. Ответ на второй вопрос. Из пропорциональности между интенсивностью поедания пищи I и скоростью размножения r следут, что Рис.3.7. Определение кинетических параметров Imax и KS по данным из таб.3.3 Задача 3.3 Условия: Исследовали кинетику размножения оленьей мыши исходя из тех же соображений, что и в задаче 3.2. Полученные данные о зависимости между плотностью распределения пищи, среднего числа коконов пильщиков на 1 м2, и средним числом коконов, съеденных одной мышью, представлены в таблице 3.4. и на рис. 3.8. Таблица 3.4. Среднее число коконов пильщиков на 1 м2 Вопросы: Проанализировать кинетику поедания коконов пильщиков оленьей мышью. Определить значения соответствующих параметров.
Рис.3.8. Зависимость между средним числом коконов пильщиков на 1 м2 и средним числом коконов, съеденных одной мышью
Решение: На первом этапе анализа обратим внимание на то, что кривая зависимости между средним числом коконов пильщиков на 1 м2 и средним числом коконов, съеденных одной мышью, представленная на рис.3.8, имеет два явно отличающихся участка. Первый начинается от нуля и заканчивается примерно на значении 40 коконов на 1 м2 и характеризуется низкими значениями интенсивности поедания. Далее идет второй участок с существенно более высокими значениями интенсивности поедания, переход одного участка в другой характеризуется четко выраженным изломом на кривой. Из этого наблюдения следует, что оленья мышь использует более сложный тип пищевого поведения. При низких плотностях пищи очевидно тип питания неспецифичен и характеризуется низким сродством к данному виду пищи. Когда же плотность пищи превышает некоторый порог, тип питания становится специфичным с повышением и сродства и скорости поедания. Для проверки данного предположения построим график Корниша-Боудена, используя данные из таблицы 3.4. Видно, что точки пересечения прямых на рис.3.9. группируются в двух различных областях. Это подтверждает предположение о двух кинетических типах пищевого поведения оленьей мыши: первый тип характеризуется высоким значением константы насыщения (низким сродством к пище) и низким значением максимальной интенсивности поедания пищи, второй тип – наоборот. Рис.3.9. График Корниша-Боудена для данных из таб.3.4. Переход от типа к типу наблюдается при плотности пищи примерно 40-50 коконов на м2 (см рис.3.8). Для определения более точных значений кинетических параметров построим графики Корниша-Боудена отдельно для каждого участка (каждого типа пищевого поведения). Очевидно, что для второго участка с высокоспецифичным типом пищевого поведения значения абсцисс нужно брать с поправкой, уменьшать на 40 единиц. Рисунки 3.10 и 3.11 демонстрируют данный подход. Таким образом, кинетика поедания коконов пильщиков оленьей мышью характеризуется наличием двух участков на оси плотности пищи: на первом участке (0-45 коконов на м2 ) кинетика низкоспецифична и имеет параметры KS 1 = 250, Imax 1 = 70, на втором участке (> 50 коконов на м2) она более специфична с параметрами KS 2 = 70, Imax 2 = 110. Рис.3.10 и 3.11. Нахождение кинетических параметров Imax и KS для двух различных участков пищевого поведения оленьей мыши. KS 1 = 250, Imax 1 = 70; KS 2 = 70, Imax 2 = 110;
 . (2.5)
. (2.5) , (2.6)
, (2.6)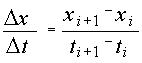 и
и  .
.![]() и
и ![]() (см. таб.2.3.), а затем построим график в этих координатах (рис.2.7). Точки на графике должны лечь на кривую, перевернутую параболу, которая пересекает ось абсцисс в точках X1 и X2, соответствующих стационарным решениям уравнения (2.5).
(см. таб.2.3.), а затем построим график в этих координатах (рис.2.7). Точки на графике должны лечь на кривую, перевернутую параболу, которая пересекает ось абсцисс в точках X1 и X2, соответствующих стационарным решениям уравнения (2.5).
 (2.7)
(2.7)
Время, год
Численность
![]()
![]()
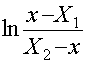
0
1120
-3,60
1
1146
1133
26,9
-3,00
2
1189
1168
42,2
-2,43
3
1253
1221
64,1
-1,90
4
1345
1299
92,4
-1,37
5
1469
1407
123
-0,85
6
1620
1544
150
-0,34
7
1783
1701
163
0,16
8
1939
1861
156
0,67
9
2072
2005
132
1,18
10
2173
2122
101
1,69
11
2245
2209
71,6
2,20
12
2292
2268
47,8
2,71
13
2323
2308
30,7
3,22
14
2342
2333
19,2
3,72
15
2354
2348
11,8
4,23

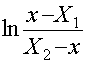 , как указано в таб.2.3. и построим график для этой переменной против переменной t (рис.2.8).
, как указано в таб.2.3. и построим график для этой переменной против переменной t (рис.2.8).

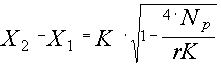 ,
,
![]() особей.
особей.
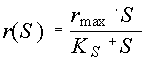 . ( 3.1)
. ( 3.1)
Время
Оптическая плотность культуры при различной концентрации субстрата (мг/л), Ex
ln (Ext /Ex0)
при различной концентрации субстрата (мг/л)50
100
200
400
800
50
100
200
400
800
0,00
0,12
0,12
0,09
0,14
0,10
-0,05
-0,01
0,01
-0,01
0,03
0,50
0,16
0,15
0,12
0,19
0,17
0,22
0,20
0,32
0,31
0,53
1,00
0,17
0,20
0,18
0,27
0,26
0,27
0,50
0,67
0,66
0,96
1,50
0,24
0,24
0,24
0,42
0,36
0,63
0,68
0,96
1,10
1,29
2,00
0,29
0,34
0,31
0,59
0,48
0,80
1,03
1,22
1,43
1,57
2,50
0,34
0,44
0,49
0,82
0,75
0,95
1,29
1,69
1,77
2,02
3,00
0,40
0,59
0,61
1,32
1,06
1,12
1,59
1,91
2,24
2,36
3,50
0,53
0,82
0,94
1,81
1,75
1,41
1,93
2,34
2,56
2,86
4,00
0,63
1,04
1,36
2,41
2,35
1,57
2,16
2,72
2,84
3,16
4,50
0,78
1,34
1,79
3,62
3,96
1,79
2,42
2,99
3,25
3,68
 Рис.3.2. Изменение оптической плотности культуры клеток E.coli при различной концентрации лимитирующего субстрата (глицерина). Здесь S50 – концентрация субстрата 50 мг/л,
Рис.3.2. Изменение оптической плотности культуры клеток E.coli при различной концентрации лимитирующего субстрата (глицерина). Здесь S50 – концентрация субстрата 50 мг/л, 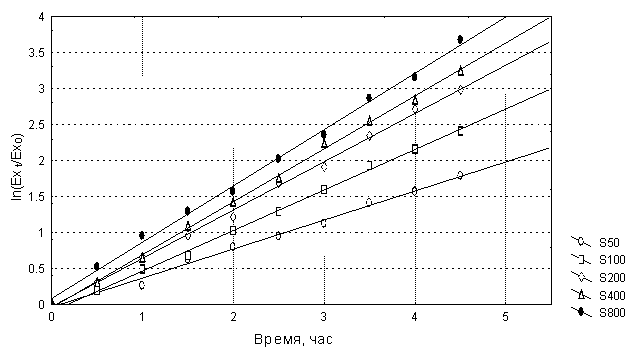
Концентрация лимитирующего субстрата S, мг/л
50
100
200
400
800
Удельная скорость размножения r, час-1
0.405
0.55
0.67
0.73
0.78


Среднее число мух на 1 м2
0
0,001
0,002
0,004
0,007
0,012
0,017
0,02
0,03
Среднее число мух, съеденных одной особью
0
5,7
9,4
14,5
18,5
21,6
23,0
23,4
25,3

 (3.2)
(3.2) . Отсюда очевидно, что половинная скорость размножения популяции, 0.5r(S), будет наблюдаться, когда плотность распределения мух S будет равна KS, т.е. 0.0038 мух/м2.
. Отсюда очевидно, что половинная скорость размножения популяции, 0.5r(S), будет наблюдаться, когда плотность распределения мух S будет равна KS, т.е. 0.0038 мух/м2.
0
10
20
40
60
100
150
200
250
Среднее число коконов, съеденных одной мышью
0
2,69
5,19
9,66
25,8
52,8
69,1
78,2
84



