Высокопроизводительные дискретные преобразования Фурье на графических процессорах
Нага К. Говидараю, Брандон Ллойд, Юрий Доценко, Бартон Смит, и Джон Манферделли Корпорация Microsoft.
Источник http://download.microsoft.com/download
Перевод Дубровина О.В.
В общем – мы представляем оригинальные
алгоритмы для вычисления дискретных преобразований Фурье с высокой
производительностью на GPU(графических
процессорах). Мы представляем иерархический, смешанный корневой алгоритмы БПФ(быстрого преобразования Фурье) для всех размерностей
преобразования – степеней двойки и не степеней двойки. Наш иерархический
алгоритм БПФ продуктивно использует разделяемую память на GPU, используя формулировку Стокхама.
Мы снизили размеры памяти при транспонировании в иерархическом алгоритме,
комбинируя транспонирование в блочный мульти-БПФ
алгоритм. Для размеров не степеней двойки, мы используем комбинацию смешанного
корневого БПФ с маленьким началом и алгоритм Блюштейна.
Мы используем модульную арифметику в алгоритме Блюштейна,
чтобы улучшить точность. Мы осуществили наши алгоритмы
используя NVDIA CUDA API и
сравнили их действие со стандартной функцией из библиотеки NVIDIA CUFFT и
оптимизированной CPU-реализацией (Intel MKL) а на
высокопроизводительном ядре с четырьмя процессорами CPU. На графическом процессоре NVIDIA мы получили производительность до 300GFlops, с усовершенствованием производительности выполнения
на 2-4 GFlops,
по сравнению со стандартными средствами средствами
CUFFT и 8-40 GFlops улучшения по сравнению с MKL для больших размеров.
Быстрое преобразование Фурье(БПФ) относится к классу алгоритмов для эффективного
вычисления дискретного преобразования Фурье(ДПФ). БПФ используется во многих областях таких как физика, астрономия, инженерия,
применяется в математике, криптографии и расчете финансов. Некоторые из этого
большого количества разнообразных приложений включают решение PDE в вычислении динамики флюидов, цифровую обработку
сигналов, и умножение больших полиномов. Из-за своей важности, БПФ используется
в нескольких эталонных тестах для параллельных компьютерных систем
таких как HPC challenge[1] NAS параллельные программы для оценки качества[2]. В этой
статье мы представляем алгоритмы для вычисления БПФ с высокой
производительностью на графических процессорах (GPU). GPU привлекательный объект для вычислений из-за его
высокой производительности и низкой стоимости. Например, графический процессор, стоимостью 300$
теоретически может предоставить предельную производительность
более 1 TFlops и предельную полосу пропускания более 100 GiBs. Овенс[3] обеспечивает
обзор алгоритмов использующих графические процессоры для общих целей. Типично, алгоритмы для общих целей для графических процессоров
должны быть спланированы под программную модель предусматриваемую графическим API. В последнее
время, тем не менее, предусматривается графическое API. В данной статье объектом нашего исследования
является NVIDIA CUDA API, так как многие
концепции расширили приложение. Главные результаты: мы представляем алгоритмы,
использованные в нашей библиотеке для вычисления БПФ различных размерностей.
Для маленьких размерностей мы вычисляем БПФ полностью в быстрой, разделяемой
памяти. Для больших размеров, мы применяем алгоритм, использующий глобальную
память или иерархический алгоритм, зависящий от размера БПФ и производительных
характеристик графического процессора. Мы поддерживаем вычисление БПФ
размерностей, не являющимися степенями двойки, используя смешанный корневой
алгоритм БПФ для маленьких оснований и алгоритм Блюштейна
для больших оснований. Мы обошли такие важные проблемы как конфликт выделения
памяти и коллизия доступа к памяти. Мы так же обошли проблему с точностью в
алгоритме Блюштейна, которая возникает при
использовании арифметики с одинарной точностью. Так же мы представляем
сравнение со стандартной библиотекой NVIDIA CUFFT
и Math
Kernel Library (MKL) от компании Intel на высокопроизводительном ПК. По данные residing в памяти GPU, наша
библиотека достигает до 300 GFlops на заводских установках часов ядра, а изменив
установки, мы получаем 340 GFlops. Мы получаем типичные улучшения производительности на
2-4 над CUFFT и 8-40 над MKL для
больших размерностей. Мы так же получили улучшение точности по сравнению с CUFFT.
II.Обзор похожих разработок
Уже существует большое количество
разработок связанных с алгоритмами БПФ, реализованных на различных
архитектурах. Соренсен и Баррус
скомпилировали базу данных с более 34000 алгоритмами эффективных алгоритмов
БПФ[8]. Мы рекомендуем читателю книгу Ван Лоана[9],
которая обеспечивает матричную структуру для понимания многих вариаций
алгоритма БПФ. Книга так же рассматриваем многие из важных проблем реализации.
Исследования, ближе всего связанные с нашей работой предполагают ускорение
вычисления БПФ, используя соответствующее аппаратуру, такую как графические или
Cell процессоры. Большинство реализаций БПФ на графических
процессорах используют графическое API,
такое как текущая версия OpenGL или DirectX[10],[11][12],[13],[14],[15]. Тем не менее, это API не поддерживает прямо рассеивания, доступ в
разделяемую память, или хорошо раздробленную синхронизацию, доступную на
современных графических процессорах. Доступ к этим характеристикам в данный
момент предоставляется только специфическими API. Библиотека компании NVIDIA для вычисления БПФ CUFFT[16], использует CUDA API[17] для
достижения более высокой производительности, чем это возможно с графическими API.
Конкурирующая работа Волкова и Казиана[17] так же
обсуждает применение CUDA. Мы так же
используем CUDA для БПФ, но мы затрагиваем
более широкий ряд входных размеров преобразования и размерностей.
Несколько разработок рассматривают
применение БПФ на процессорах Cell
[18],[19],[20],[21],[22]. Наши результаты для больших размеров преобразования
на множестве графических процессоров значительно выше, чем опубликованные
результаты для процессоров Cell.
III. Обзор Графических процессоров и БПФ
В данной статье мы сосредотачиваемся в
основном на графических процессорах NVIDIA,
несмотря на существование многих устройств и
технических новинок и в других архитектурах.
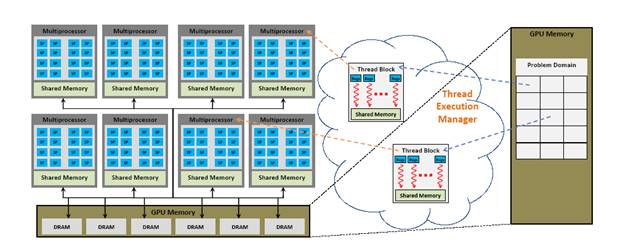
Рисунок 1 – Аппаратная
модель NVIDA
GeForce 8800 GPU
Графический процессор состоит из
большого количества скалярных процессоров, которые могут выполнять одну
программу при параллельном использовании с помощью потоков. Скалярные
процессоры группируются вместе в мультипроцессоры, у каждого процессора есть
несколько разделенных связанных потоков, и в каждый момент, группа потоков вызывается в warp
и выполняются на мультипроцессоре. Когда несколько warp назначены на мультипроцессор, память скрывается и
переключается на другой warp. У каждого мультипроцессора есть большой файл
регистра. Во время выполнения, программные регистры располагаются на потоках,
назначенных на мультипроцессор. У каждого мультипроцессора так же есть
небольшое количество разделяемой памяти, которая может быть использована для
связи между потоками, выполняющимися на скалярном процессоре. Иерархия памяти
графического процессора разработана для максимальной скорости передачи данных в
глобальную память, которая видима для всех мультипроцессоров. У разделяемой
памяти низкий уровень скрытости. Она организована в нескольких местах чтобы обеспечить высокую скорость передачи данных. На
высшем уровне, вычисления на графическом процессоре
происходят следующим образом. Пользователь выделяет память на графическом
процессоре, копирует данные на графический процессор, определяет программу,
которая выполняется на мультипроцессоре и после выполнения, копирует данные
обратно на хост. Для того, чтобы выполнить программу
на домене, пользователь разбивает домен на блоки. Менеджер выполнения потоков
потом назначает потоки для выполнения на блоке и записывает выходные данные в
глобальную память.
Обзор БПФ
Обратное дискретное преобразование Фурье
(ДПФ) комплексной последовательности x=x0, .. xN-1 это N-точечное преобразование где Хк=
Обратное ДПФ определяется как. Обычное
преобразование ДПФ требует О(N2) операций, и может быть достаточно затратным.
Алгоритмы БПФ вычисляют ДПФ за О(N log N) операций. Благодаря меньшему
количеству вычислений с числами с плавающей точкой на каждый элемент, БПФ может
иметь более высокую точность, чем обычное ДПФ. Детальный обзор различных
алгоритмов БПФ может быть найден в Ван Лоан[9]. В
данной статье детально рассматриваются алгоритмы БПФ для комплексных входных
данных произвольного размера на графических процессорах.
Выполнение БПФ на графических процессорах
Предаставление алгоритмов БПФ может зависеть от строения памяти
подсистемы и того, как хорошо она эксплуатируется. Так же графические
процессоры предоставляют высокую степень параллелизма, этап перемещения
индексов для алгоритма БПФ такого как алгоритм Кули-Тьюки может быть достаточно затратным из-за
непоследовательности доступа к памяти. В данной статье, мы убрали этап
перемещения индексов, используя формулировку Стокхема
для БПФ.
1 float2*
CPU_FFT(int N, int R,
2 float2* data0, float2* data1) {
3 for( int Ns=1; Ns<N; Ns*=R ) {
4 for( int j=0; j<N/R; j++ )
5 FftIteration( j, N, R, Ns, data0, data1
);
6 swap( data0, data1
);
7 }
8 return data0;
9 }
10
11 void GPU_FFT(int
N, int
R, int
Ns,
12 float2* dataI, float2* dataO) {
13 int j = b*N + t;
14 FftIteration( j, N, R, Ns, dataI, dataO );
15 }
16
17 void FftIteration(int j, int N, int R, int Ns,
18 float2* data0, float2*data1){
19 float2 v[R];
20 int idxS = j;
21 float angle = -2*M_PI*(j%Ns)/(Ns*R);
22 for( int r=0; r<R; r++ ) {
23 v[r] = data0[idxS+r*N/R];
24 v[r] *= (cos(r*angle), sin(r*angle));
25 }
26 FFT<R>( v );
27 int idxD = expand(j,Ns,R);
28 for( int r=0; r<R; r++ )
29 data1[idxD+r*Ns] = v[r];
30 }
31
32 void FFT<2>( float2* v ) {
33 float2 v0 = v[0];
34 v[0] = v0 + v[1];
35 v[1] = v0 - v[1];
36 }
37
38 int expand(int idxL, int N1, int N2 ){
39 return (idxL/N1)*N1*N2 + (idxL%N1);
40 }
Рисунок 2 – Показывает
псевдокод для алгоритма Стокхама с основанием R с особенностью для основания 2.
Это, однако, требует что мы
выполните неуместное FFT. Рис. 2
показывает псевдокод для основания R
Stockham FFT со специализацией для основания системы счисления 2.
В каждой итерации, об алгоритме можно предусмотреть объединения R FFTs на подпоследовательностях
длины N, в FFT новой
последовательности длины RNs, выполняя FFT длины R на соответствующих элементах подпоследовательностей.
Производительность традиционных реализаций GPGPU FFT использование API графики ограничена
нехваткой рассеивания операции, то есть, поток не может осуществлять запись в
произвольное местоположению в памяти. Псевдокод, показанный на Рис. 2,
записывает в R различные местоположения на
каждой итерация (строка 29). Без разброса, R значения должны считаться для каждого
сгенерированного вывода, а не чтение R
оценивает для каждых выводов R [14]. GPUs и API, которые
поддерживают запись многих значений в одно и то же место в множественных буферах
могут сохранять избыточные чтения, но должны также использовать более сложную
индексацию, обращаясь к записанным значениям в предыдущей итерации, или после
каждой итерации, они должен скопировать значения в их надлежащее местоположению
в отдельной итерации [15], которая зависит от полосы пропускания. Таким
образом, рассеивание важно для того, чтобы сохранить полосу пропускания памяти.
Рисунок 2 также показывает псевдокод для реализации FFT на GPU, который
поддерживает рассеивиние. Основное различие между GPU_FFT () и CPU_FFT () то, что
индекс j
в данных сгенерирован как функция числа
потока t, блочный индекс b, и число потоков за блок T (строка 13). Кроме того, итерация по значениям Ns сгенерирована множественными запросами GPU_FFT (), а не в
цикле (строка 3), потому что глобальная синхронизация между потоками необходима
между итерациями, и для многих GPUs единственное глобальная синхронизация - ядерное
завершение.
Для каждого запроса GPU_FFT (), T установлен в N=R и номер блоков потока B равно М., где М
- это число FFTs, которые обрабатываются одновременно. Обработка многомерных FFTs в то же самое время важно
потому что число warp, используемых для маленьких
мощностей установленного по размеру FFTs, возможно, не достаточно для достижения полного
использования многопроцессорной системы, либо для скрытия от памяти время
ожидания, обращаясь к глобальной памяти. Обработка больше чем одного FFT приводит к большему количеству warp и облегчает эти проблемы.
Несмотря на то, что GPU_FFT использует рассеивание, в ней все еще много проблем
производительности. Во-первых, при записи у памяти есть проблемы объединения.
Попытки подсистемы памяти объединить память от множественных потоков в меньшее
число доступов к большим блокам памяти. Но пространство между последовательными
доступами, сгенерированными вначале немного итераций (маленький Ns) являются слишком большими для эффективного
объединения (строка 29). Во-вторых, алгоритм не эксплуатирует низкое время
ожидания разделяемая память, чтобы улучшить многократное использование данных.
Это также проблема для традиционных реализаций GPGPU, потому что API
графики не обеспечивает доступ к общедоступной памяти. Наконец, чтобы
обработать данные произвольной длины, мы нуждались бы в написании отдельной
специализации для всех возможных корней R. Это непрактично, особенно для больших R. В следующей секции мы обсудим, как мы решаем
каждую из этих проблем.
Поскольку GPUs отличаются по
размерам разделяемой памяти, памяти, и конфигурации процессора, алгоритмы FFT
должен быть идеально параметризуйтесь и автонастроены через различные варианты
алгоритмов и архитектуру.
Выводы и планы на будущее
Мы представили несколько алгоритмов для
эффективного вычисления БПФ произвольной длины и размерности на графических
процессорах. Мы выбрали алгоритм, который предоставляет лучшую
производительность для полученного входного размера и конфигурации аппаратуры.
Наш иерархический алгоритм БПФ минимизирует количество доступов к памяти,
совмещая операции транспонирования с вычислением БПФ. Мы так же избежали
проблем с точностью. Наши результаты показывают существенное улучшение
производительности по сравнению с алгоритмами БПФ, основанными на графических и
обычных процессорах. Есть еще несколько направлений для дальнейшей работы. Мы
хотели бы расширить нашу библиотеку использованием чисел с двойной точностью.
Еще одна важная проблема – вычисление математических функций. Функции cos() и sin() сейчас
гораздо более затратные при использовании чисел двойной точности, чем при одинарной. Для этого возможно лучше использовать заранее
вычисленную таблицу со значениями этих функций. Мы так же хотели бы добавить
поддержку графических процессоров и другими производителями, применяя нашу
библиотеку, используя DirectX 11 Compute Sharder APi. Другим интересным направлением является выполнение
БПФ на нескольких графических процессорах.
Литература
1. “HPC challenge,”
http://icl.cs.utk.edu/hpcc/, 2007.
2. “NAS parallel benchmarks,”
http://www.nas.nasa.gov/Resources/Software/npb.html, 2007.
3. J. D. Owens, D. Luebke, N. Govindaraju, M.
Harris, J. Kr.uger, A. E. Lefohn,
and T. Purcell, “A survey of general-purpose computation on graphics hardware,”
Computer Graphics Forum, vol. 26, no. 1, pp. 80–113, Mar. 2007.
4. “ATI CTM Guide,”
Advanced Micro Devices, Inc., 2006.
5. NVIDIA CUDA:
Compute Unified Device Architecture, NVIDIA Corp.,2007.
6. C. Boyd, “The
DirectX 11 compute shader,” http://s08.idav.ucdavis.edu/boyd-dx11-compute-shader.pdf,
2008.
7. A. Munshi, “OpenCL,” http://s08.idav.ucdavis.edu/munshi-opencl.pdf,
2008.
8. H. V. Sorensen
and C. S. Burrus, Fast Fourier Transform Database. PWS Publishing, 1995.
9. C. V. Loan,
Computational Frameworks for the Fast Fourier Transform. Society
for Industrial Mathematics, 1992.
10. K. Moreland and
E. Angel, “The FFT on a GPU,” in Proceedings of the ACM SIGGRAPH/EUROGRAPHICS
Conference on Graphics Hardware, 2003, pp. 112–119.
11.
J. Spitzer, “Implementing a GPU-efficient FFT,” SIGGRAPH Course on Interactive
Geometric and Scientific Computations with Graphics Hardware, 2003.
12. J. L. Mitchell,
M. Y. Ansari, and E. Hart, “Advanced image processing
with DirectX 9 pixel shaders,” in ShaderX2: Shader Programming Tips and Tricks with DirectX 9.0, W.
Engel, Ed. Wordware Publishing, Inc., 2003.
13. T. Jansen, B.
von Rymon-Lipinski, N. Hanssen,
and E. Keeve, “Fourier volume rendering on the GPU using a split-stream-FFT,”
in Proceedings of the Vision, Modeling, and Visualization Conference 2004,
2004, pp. 395–403.
14
T. Sumanaweera and D. Liu, “Medical image
reconstruction with the FFT,” in GPU Gems 2, M. Pharr, Ed. Addison-Wesley,
2005, pp. 765–784.
15
N. K. Govindaraju, S. Larsen, J. Gray, and D. Manocha, “A memory model for scientific algorithms on
graphics processors,” Supercomputing 2006, pp. 6–6, 2006.
16. CUDA CUFFT
Library, NVIDIA Corp., 2007.
17. V. Volkov and B. Kazian, “Fitting
FFT onto the G80 architecture,” http://www.cs.berkeley.edu/_kubitron/courses/cs258S08/projects/reports/project6report.pdf
18. A. C. Chow, G.
C. Fossum, and D. A. Brokenshire,
“A programming example: Large FFT on the cell broadband engine,” Whitepaper,
2005.
19.
L. Cico, R. Cooper, and J. Greene, “Performance and
programmability of the IBM/Sony/Toshiba Cell broadband engine processor,”
Whitepaper, 2006.
20. S. Williams, J.
Shalf, L. Oliker, S. Kamil, P. Husbands, and K. Yelick,
“The potential of the cell processor for scientific computing,” in CF ’06:
Proceedings of the 3rd Conference on Computing Frontiers, 2006, pp. 9–20.
21 D. A. Bader and
V. Agarwal, “FFTC: fastest Fourier transform for the
IBM Cell broadband engine,” 14th IEEE International Conference on High
Performance Computing (HiPC), pp. 172–184, 2007.
22.
M. Frigo and S. G. Johnson, “FFTW on the cell
processor,” http://www.fftw.org/cell/index.html
, 2007.
23. D. H. Bailey, “FFTs in external or hierarchical memory,” Supercomputing,
pp. 23–35, 1990.