ОПТИМИЗАЦИЯ РАСПИСАНИЙ РАБОТЫ АВТОМАТИЗИРОВАННЫХ ТЕХНОЛОГИЧЕСКИХ КОМПЛЕКСОВ МЕХАНООБРАБОТКИ С ИСПОЛЬЗОВАНИЕМ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ
С.В. Лаздынь, А. И. Секирин
каф. АСУ ДонНТУ, Донецк, Украина
Источник:Международный сборник научных трудов “Прогрессивные технологии и системы машиностроения”, выпуск 25. –Донецк: ДонНТУ.-2003. –С. 198-203
The new approach in calculation of the suboptimum schedules of the automated technological complexes for mechanical processing with use of genetic algorithms and object-oriented models is offered. For effective work of genetic algorithm the problem-oriented operators of crossingover and mutation are developed, the computer experiments are executed.
Одним из важных направлений развития машиностроительных производств является повышение уровня автоматизации обрабатывающего и вспомогательного оборудования с использованием современных компьютерных технологий и создание на этой базе автоматизированных технологических комплексов (АТК).
С точки зрения управления АТК представляет собой сложный динамический объект, на функционирование которого оказывают влияние ряд возмущающих факторов, таких как поломки оборудования, отсутствие заготовок и инструмента, директивные производственные задания и др. Поэтому, для эффективной эксплуатации таких объектов одной из главных задач является формирование оптимального или близкого к нему расписания работы оборудования, а также - динамическая его корректировка с учетом изменения производственной ситуации. При этом необходимо наличие модели АТК, которая обеспечит достаточно точное отображение протекающих в нем процессов функционирования производственного оборудования и движения материальных потоков во времени и пространстве.
Принимая во внимание сложность АТК как объекта моделирования, многообразие его модификаций и реализаций для изготовления различных типов деталей и узлов и с учетом проведенного анализа ранее применяемых методов моделирования, для построения модели АТК авторами предложено использовать объектно-ориентированный подход (ООП) [1]. Учитывая модульный принцип построения АТК, в качестве объектов моделирования выбраны следующие типовые элементы АТК: гибкий производственный и транспортный модули, автоматизированный склад и система управления АТК. Для этих типовых элементов разработаны соответствующие классы объектов. Реализован алгоритм и программа объектно-ориентированной модели и произведена её экспериментальная проверка на реальных производственных данных.
Анализ показал, что не смотря на проведенные исследования и разработки, задача получения оптимальных расписаний работы АТК не решена. Оптимальные решения получены лишь для простейших случаев. Для получения приемлемых решений в допустимые сроки в основном применяются эвристические методы, построенные на использовании различных правил запуска деталей в обработку. Метод полного перебора невозможно применять, так как сроки получения решения превышают допустимые.
Для оптимизации расписаний работы АТК предлагается использовать генетические алгоритмы (ГА), в основу которых положено эволюционное развитие и наследование свойств особей (решений, кодированных хромосомами) [2]. Механизм развития и наследования позволяет последовательно улучшать хромосомы в каждой новой популяции, что приводит к получению субоптимальных (близких к оптимальным) решений.
Особенностью предлагаемого подхода является совместное использование объектно-ориентированной модели и генетических алгоритмов, что позволит оптимизировать очередность и размеры партий запуска при выполнении директивных сроков выпуска деталей. На выходе модели АТК формируется таблица результатов в виде последовательности событий и основных показателей работы АТК (длительность технологического цикла, коэффициенты загрузки оборудования, длительность простоев оборудования и т.д.), которая является основой нового расписания. Эти данные являются ответом моделирующей системы на входные параметры, посланные ГА. Их можно интерпретировать как фитнесс (целевую функцию – fц) для конкретной хромосомы. Обобщенная схема поиска оптимального расписания с использованием объектно-ориентированной модели и генетических алгоритмов показана на рис.1.
В процессе работы генетический алгоритм формирует множество возможных решений (популяцию хромосом). Предлагается использовать двухуровневое представление хромосом, что позволит варьировать не только последовательность запуска партий деталей, но и размерами этих партий:
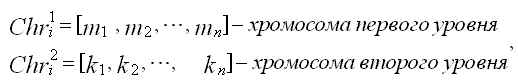
mi и ki – натуральные числа (биты хромосом), кодирующие номера и размерности партий запуска соответственно;
N – размер популяции.
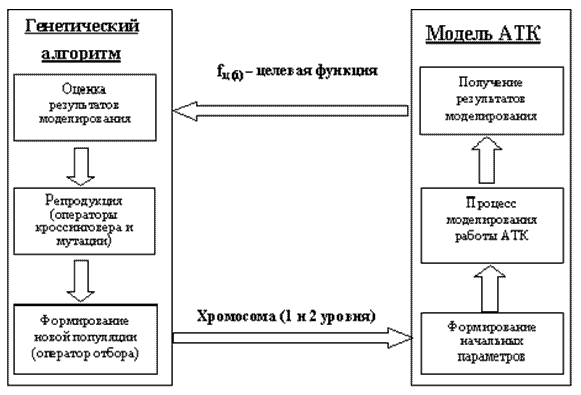
Рис. 1. Обобщенная схема поиска оптимального расписания
Первый (или верхний) уровень хромосом кодирует различные варианты последовательностей запуска деталей по их типам на технологический участок. Каждой хромосоме первого уровня сопоставляется хромосома второго уровня, в которой содержится информация о величине партий запуска для каждого типа детали. Длина хромосомы определяется номенклатурой обрабатываемых деталей, которые будут принимать участие в процессе оптимизации. Каждой отдельной разновидности детали присваивается свой уникальный код, представленный натуральным числом. Последовательность этих кодов (стринг) в хромосоме определяет очередность запуска деталей в производство.
Для эффективной работы ГА разработаны проблемно-ориентированные операторы кроссинговера и мутации. Сравнение описаний различных генетических алгоритмов данных Гольдбером, Холландом и Девисом [2], показывает, что в них реализована одна основная идея моделирования эволюции с некоторыми модификациями.
Для оптимизации расписаний стандартный оператор кроссинговера (ОК) не может быть применен. При выполнении стандартного ОК с высокой степенью вероятности возможно нарушение ограничений на построение хромосомы, а именно возможно получение стринга, в котором будут присутствовать повторяющиеся элементы. Этот недостаток можно ликвидировать, воспользовавшись методом «жадного кроссинговера», который заключается в том, что напрямую в формировании потомков принимают участие только первые части хромосом. Каждый потомок достраивается отдельно, при этом каждый следующий элемент стринга выбирается из вторых частей родителей, а если это нарушает условия формирования хромосомы, то из всех оставшихся, который потенциально могут принять участие формировании потомка, т.е. ещё не были использованы. Этот метод позволяет избежать некорректного представления хромосом.
С целью устранения описанных выше недостатков были проанализированы несколько подходов в реализации ОК, и для решаемой задачи была разработана модификация двухточечного кроссинговера. Как и для простого ОК, на первом шаге (рис. 2.) из всей популяции выбираются две хромосомы-родителя. Далее определяются две точки кроссинговера, которые выбираются по следующим правилам:
- - Позиция первой точки ОК k1 э [ 1 , N-1-Lблока ] (Lблока – это минимальное расстояние между точками кроссинговера, N – длина хромосомы);
- - Позиция второй точки ОК k2 э [ k1 + Lблока , N-1 ].
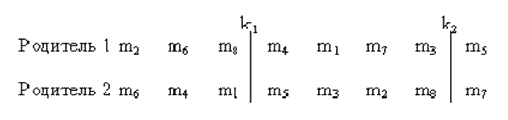
Рис 2. Определение точек кроссинговера для выбранных хромосом
На этом этапе ОК известны части хромосомпотомков только между точками кроссинговера. Поскольку эти элементы принадлежат хромосомам, удовлетворяющим критериям формирования хромосом, то данные участки также удовлетворяют этим критериям. В процессе формирования дочерних хромосом возможно возникновение конфликта повторяемости элементов стринга. В связи с этим необходим четкий механизм замены некорректных участков хромосомы. Для этого строится цепочка преобразований на основе известных участков хромосомы (Рис.3а):
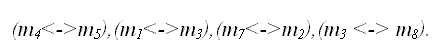
Если при формировании потомка будет предпринята попытка использовать уже задействованный в нем элемент, то он будет заменен на указанный в серии преобразований. Обмен первыми битами показан на рис.3б. После обмена проверяется корректность хромосом-потомков при таком наборе элементов. Как видно, первый потомок не вызывает конфликта. Для второго же потомка значение m2 встречается дважды (позиция 1 и 6). Производим над позицией 1 преобразование, согласно серии, созданной на втором шаге. (m7<->m2) – такая замена первому элементу присвоит значение m7. При таком наборе оба потомка корректны и возможно дальнейшее заполнение элементов хромосом-потомков. Поступая аналогичным образом заполняют оставшиеся позиции хромосом-потомков. Результат работы модифицированного оператора кроссинговера показан на рис.3в.
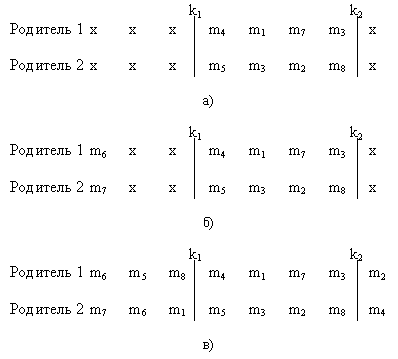
Рис 3. Поэлементное формирование потомков с коррекцией
Качество функционирования алгоритма в значительной степени зависит от эффективного применения оператора мутации (ОМ). Поскольку при стандартной мутации предполагается замена мутирующего сегмента другим значением, а ограничения на формирование хромосом не позволяют этого сделать, то за основу был принят модифицированный ОМ при котором происходит обмен значениями между двумя случайно выбранными сегментами хромосомы.
Используя проблемно-ориентированные операторы кроссинговера и мутации составлен генетический алгоритм. Программная реализация объектно-ориентированной модели и модуля поиска субоптимального расписания работы АТК на базе генетического алгоритма выполнена с помощью языка визуального программирования Delphi 6.0. В результате проведенных экспериментальных исследований с использованием реальных производственных данных АТК с помощью генетических алгоритмов получены решения близкие к оптимальным (для сравнения применялся метод полного перебора, позволяющий получить оптимальное решение).
Проведенные исследования показали целесообразность и эффективность применения данного подхода в управлении автоматизированными технологическими комплексами. Применение генетических алгоритмов позволяет получать близкие к оптимальным решения в допустимые сроки.
Литература
1. Лаздынь С.В., Секирин А.И. Объектно-ориентированный подход в моделировании автоматизированных технологических комплексов механообработки //Материалы третьей Всеукраинской конференции молодых ученых ”Інформаційні технології в науці, освіті і техніці”. – Черкасы: ЧГТУ, 2002, с 243-246.
2. Курейчик В.М. Генетические алгоритмы. Монография. Таганрог: Изд. ТРТУ, 1998, 242с.