Бернд Зондек Перевод с английского Ивко ЕЕ Численное моделирование случайных процессов

Численное моделирование случайных процессов

Бернд Зондек

Перевод с английского: Ивко Е. Е.

Источник: Proc. 2003 Winter Simulation Conf., New Orleans, LA, 2003.
http://www.dtic.mil/cgi-bin/GetTRDoc?AD=AD736614&Location=U2&doc=GetTRDoc.pdf

Предисловие

Случайные процессы используются для представления разнообразных явлений. В этом докладе описывается генератор случайных процессов, полезный для исследований моделирования с помощью компьютера. Этот доклад был рассмотрен Джоном Х. Уолкером, Дж.

Реферат

Метод был получен для моделирования одномерных стационарных случайных процессов с автокорреляционной функцией, заданной конечной тригонометрической суммой. Коэффициенты последней – некоррелированные случайные числа. Дается строгая оценка степени приближения к автокорреляционной функции. Метод является достаточно общим и не требует спектральной функции для того, чтобы быть рациональным.

Содержание

Предисловие

Реферат

Введение

Моделирование одномерного стационарного в широком смысле случайного процесса с заданным средним и автокорреляцией

Пример

Апроксимирует ли процесс процесс ?

Стационарность и нормальность в узком смысле

Заключение

Ссылки

1. Введение

Случайные процессы [1, 2] используются для представления явлений в самых различных областях.

Имеет важное значение располагать вычислительными алгоритмами генерации случайных процессов для проведения исследований по моделированию на компьютере.

В настоящем докладе мы будем придерживаться условия выделения всех вероятностных величин.

В общих чертах метод использует сочетание независимых случайных величин для генерации стационарного случайного процесса с определённой автокорреляцией. Таким образом, можно моделировать процесс на ЭВМ с помощью «генератора случайных чисел». Этот доклад ограничивается обсуждением одномерных стохастических процессов.

2. Моделирование одномерного стационарного в широком смысле случайного процесса с заданной автокорреляцией

Пусть среднее стационарного процесса равно нулю, а автокорреляция – . Спектральная функция [1, стр. 338] задана следующим образом:

Обратная связь:

Мы имеем здесь и сразу предполагали, что линейчатого спектра нет.

Теперь мы можем построить стохастический процесс , который имеет данное среднее, обладает примерно данной функции автокорреляции и зависит только от числа дискретных случайных величин. Мы продолжаем путем деления частотного диапазона на отдельные промежутки времени. Обозначим размер интервала . Это приращение должно быть небольшим в некотором смысле, чтобы быть определено позднее. Определим величины:

Эти величины, очевидно, неотрицательны и представляют энергии в диапазоне частот от 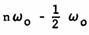до . Теперь возьмём дискретный набор комплексных случайных величин, удовлетворяющих:

Сейчас, конечно, эти условия не определяют случайные величины однозначно. Однако все случайные процессы, определяющиеся следующим образом:

обладают некоторыми общими свойствами. У нас есть

Таким образом, процессы имеют такое же среднее и суммарную мощность, как процесс .

Исследуем теперь автокорреляцию . Из формул. (7), (8) мы имеем:

Таким образом, стационарны в широком смысле, но их автокорреляционная функция отличается от . Оценим разницу. Насколько хорошо аппроксимирует ? Мы можем написать:

Каждое слагаемое в (13) может быть записано как:

Поэтому мы можем написать для разницы требуемой и моделируемой автокорреляционных функций:

Величина окончательного выражения может быть легко оценена. Когда:

Мы имеем неравенство:

Следовательно, по теореме интегрального исчисления о первом среднем, мы имеем следующее неравенство:

Уравнение (15), таким образом, дает неравенство:

Как видно из этого неравенства, для того, чтобы аппроксимировать в диапазоне , мы должны выбрать приращение частоты , такое, чтобы:

Кроме того, мы видим, что какое бы малое мы не выбрали, не будет аппроксимировать для всех . Это связано с тем, что процесс включает в себя только дискретный набор частот.

Неравенство (19) дает нам эффект дискретизации частоты на автокорреляционную функцию. Для целей численного моделирования мы должны также оценить влияние обрыва ряда в (9). В отличие от частоты дискретизации, обрыв влияет на полную мощность в соответствии с уравнением (11). Если мы обрываем после , мощность будет сокращена в соответствии с (11):

3. Пример

Допустим, мы хотим имитировать случайный процесс с автокорреляционной функцией:

Его спектральная функция [1, с. 340]:

Суммарная мощность:

Мы можем определить корреляционную разность как:

Допустим, мы хотим представить автокорреляционную функцию с точностью до от полной мощности через разность m корреляционных разностей. Максимальная задержка задается следующим выражением:

Ошибка в автокорреляционной функции из-за дискретизации удовлетворяет, в соответствии с формулой (19):

Ошибка, связанная с обрывом, удовлетворяет в соответствии с формулой (21):

Тогда:

И таким образом:

Требуется, чтобы:

Мы хотели бы, чтобы это равенство удовлетворялось как можно меньшим значением N. Минимизация выражения слева с учетом дает:

Подстановка этого значения в (31) даёт:

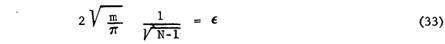
или:

Если, например, мы хотим точность 10% при 100 корреляционных разностях, число необходимых членов:

4. Аппроксимирует ли процесс процесс ?

Мы могли бы склоняться к тому, чтобы думать, что процесс , построенный упомянутым выше образом, аппроксимирует в некотором смысле процесс . Однако это справедливо, только если (см. [1, с. 461]):

удовлетворяет всем условиям, выраженным (4) – (8) и процесс тогда аппроксимирует в среднеквадратичном смысле, как описано в ссылке.

5. Стационарность и нормальность в узком смысле

Может быть полезно для некоторых приложений иметь возможность генерировать случайные процессы, стационарные в узком смысле. Случайные процессы , как определено формулами (3) – (9), в большинстве стационарны только в широком смысле. Мы можем показать это, рассматривая следующий пример. Запишем:

где:

Пусть и – взаимно независимые случайные величины. Пусть имеет следующую плотность вероятности:

Пусть удовлетворяет:

и пусть:

где – любое сочетание чисел, не всех равных нулю. Из этого следует, что уравнения (4) – (8) выполнены и процесс:

стационарен в широком смысле. Однако он не стационарен в узком смысле, что может быть показано, если заметить, что:

что не является константой.

Может быть показано, что если и взаимно независимы, удовлетворяют уравнениям (39), (42) – (44) и равномерно распределены на интервале от до и удовлетворяют уравнению (40), процесс , описанный уравнением (46), является стационарным в узком смысле.

Можно генерировать нормальный процесс описанным методом (для существования нормальных процессов см. [2, c. 72]. В этом случае стационарность в широком смысле подразумевает стационарность в узком смысле. Нормальность часто принимается, если моделируемый процесс является не до конца известным. Различные теоретические результаты, касающиеся образцовых распределений, могут быть получены для нормального процесса.

Чтобы генерировать нормальный процесс, запишем:

Мы можем переписать (9) как:

Выберем и как взаимно независимые нормальные случайные величины, удовлетворяющие:

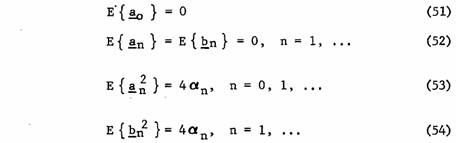
Эти уравнения заключают в себе уравнения (4) – (8). Теперь, так как является линейной комбинацией нормальных случайных величин, это нормальный процесс и стационарный в узком смысле.

Мы можем доказать, что нормальный процесс, который мы только что описали обладает свойством «случайной фазы», а именно случайные величины , определённые как:

взаимно независимы и распределены равномерно. Действительно, случайная величина:

распределена в соответствии с распределением Стьюдента с одной степенью свободы [3, c. 237].

Распределение Стьюдента сводится для одной степени свободы к распределению Коши [3, с. 246]. Плотность вероятности:

Отсюда легко вывести, что плотность вероятности для :

От случайных фаз часто требуют представления различных явлений во временной области.

6. Заключение

Мы представили метод для моделирования стационарных случайных процессов численно. Метод является достаточно общим и не зависит от спектральной функции, являясь рациональным. Он требует только генератор случайных чисел и необходимую вычислительную мощность.

Ссылки

Athanasios Papoulis. Probability, Random Variables, and Stochastic Processes. – McGraw-Hill, 1965.
J. L. Doob. Stochastic Processes. – John Wiley, 1967.
Harold Cramer. Mathematical Methods of Statistics. – Princeton, 1958.