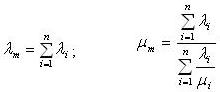
2. Параллельное соединение:
Источник: Журнал «Электричество» №10, 1985. - с. 12-14
Предлагаемый метод расчета показателей надежности восстанавливаемых систем электроснабжения отличается от существующих [1,2,3] тем, что не требует составления логической схемы замещения минимальных сечений. Для простых схем систем электроснабжения, состоящих из последовательного, параллельного либо смешанного соединения определяются по формулам:
1. Последовательное соединение:
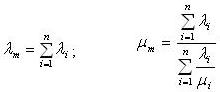
2. Параллельное соединение:

Формулы (1) и (2) справедливы, когда функционирование элемента системы можно описать с помощью чередующихся интервалов времени работы:
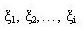 и пробоя
и пробоя  . Случайные интервалы времени
. Случайные интервалы времени  и
и 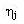 не противоречат экспоненциальной функции распределения, т.е.
не противоречат экспоненциальной функции распределения, т.е.
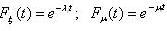 Все величины
Все величины  и
и 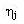 взаимно независимы и выполняется условие:
взаимно независимы и выполняется условие:

Результаты исследования.
Схемы замещения системы электроснабжения не всегда состоят из последовательного, параллельного или смешанного соединения элементов. Существуют и более сложные схемы– мостиковые[1]. Под системой электроснабжения со сложной схемой будем понимать такую схему, в состав которой входят хотя бы одна группа элементов, имеющих мостиковую схему.
Для таких схем предлагается использовать способ преобразования «треугольник-звезда». Этот способ отличается от известного [4] тем, что позволяет производить преобразование сложных схем замещения с учетом восстановления элементов и сроков их диагностики.
Сущность предлагаемого преобразования «треугольник-
звезда» состоит в том, что соединение элементов в виде треугольника заменяется эквивалентным по надежности соединением
в виде звезды, т.е. задача сводится к определению эквивалентных интенсивностей отказов и восстановлений «звезды» через
аналогичные параметры надежности «треугольника».
На рис. 1.а,б изображены две схемы соединения элементов — треугольник и звезда. Пусть каждый элемент треугольника имеет интенсивности отказов 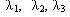 и восстановлений
и восстановлений 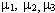 Аналогичные параметры надежности имеет и звезда
Аналогичные параметры надежности имеет и звезда
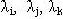 и восстановлений
и восстановлений
 .
.
Приведенные структуры будут эквивалентными по надежности, если интенсивности отказов и восстановлений между узлами 1-3, 1-2, 2-3 треугольника будут равны интенсивностям отказов и восстановлений между соответствующими узлами звезды. Между узлами 1-3 треугольника один путь проходит через элемент 1, а второй - через элементы 2 и 3. Для узлов
1-3 звезды имеется только один путь через элементы і и k. Схемы замещения приведены на рис. 1.в. Аналогичным образом составляются схемы замещения и для путей 1-2 и 2-3 треугольника и звезды (рис. 1,г,д).
Используя полученные схемы замещения, с помощью формул (1), (2) определяются эквивалентные интенсивности отказов
и восстановлений для всех путей успешного функционирования
элементов треугольника и звезды. Приравняв соответствующие интенсивности отказов и восстановлений путей успешного функционирования элементов треугольника и звезды, получим систему из шести линейных алгебраических уравнений:

Выразив интенсивности отказов
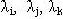 и восстановлений
и восстановлений
 элементов звезды через интенсивности отказов и восстановлений элементов треугольника, получим:
элементов звезды через интенсивности отказов и восстановлений элементов треугольника, получим:
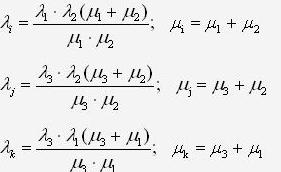
Если требуется обратный переход от звезды к труегольнику, то, используя эту же систему уравнений (3), получим:

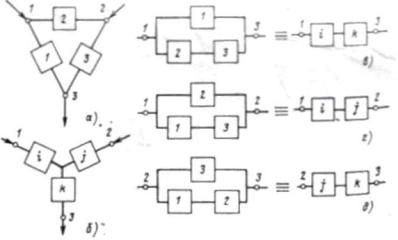
Рис.1 - Схемы треугольника и звезды
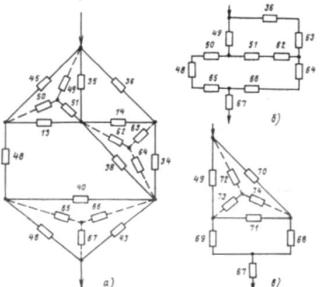
Рис.2 - Показатели надежности схемы
Расчет надежности сложных схем систем электроснабжения
с учетом восстановления элементов и с применением преобразования «треугольник — звезда» менее трудоемок по сравнению
с применяемыми в настоящее время методами, требующими составления специальных схем замещения минимальных сечений.
Литература
1. Рябинин И. А. Основы теории и расчета надежности судовых электроэнергетических систем.— 2-е изд. Л.: Судостроение. 1971, c. 58-62
2. Константинов Б. А., Лосев Э. А. Логико-аналитический метод расчета надежности восстанавливаемых систем электроснабжения.—Электричество, 1971, № 12, с. 21-25
3. Фокин Ю. А., Чан Динь Лонг. Структурный анализ и методы оценки надежности сложных систем электроснабжения.— Электричество, 1973. № 5, с. 4-6
4. Козлов Ю. А., Ушаков И. А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики.— М.: Советское радио, 1975, с. 105-107