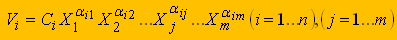 (1)
(1)Обеспечение качества обработанной поверхности с достижением минимальной себестоимости механической обработки - важнейшая задача, решаемая при проектировании технологических процессов изготовления деталей. Одним из резервов снижения себестоимости является выбор рациональных параметров процесса резания. В связи с этим весьма актуальны исследования по определению оптимальных режимов резания, обеспечивающих для заданных условий обработки и требований к качеству обработанных поверхностей минимальную себестоимость.
Основное требование МГП состоит в том, что все компоненты задачи оптимизации должны быть выражены количественно в виде обобщенных положительных поли-номов, называемых позиномами, от управляемых параметров. Возможность использования МГП для оптимизации режимов резания обусловлена тем, что целевая функция и ограничения могут быть представлены в виде суммы компонентов, каждый из которых выражается степенной функцией:
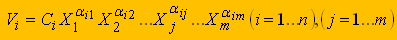 (1)
(1)В соответствии с МГП задачи оптимизации формулируются следующим образом:
 при ограничениях
при ограничениях 
 при ограничениях
при ограничениях 
В этих выражениях g(x) - прямая функция, V(W) –двойственная функция, V(W), Wi - положительные веса.
В противоположность другим методам оптимизации в МГП вначале находят экстремум целевой функции и относительный вклад каждой компоненты в его значение, а затем - оптимальные значения переменных параметров.
В представляемой работе в качестве критерия оптимизации принимается переменная часть себестоимости обработки детали режущим инструментом за один проход, зависящая от режимов резания:
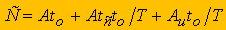 (2)
(2)Целевая функция, выражающая зависимость переменной части себестоимости от режимов резания, с учетом известных соотношений основного времени обработки и стойкости инструмента с режимами, имеет вид
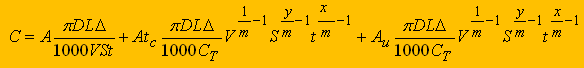 (3)
(3)В настоящей работе решается задача двухпараметрической оптимизации, то есть задача определения оптимальных значений скорости резания и подачи при заданной глубине резания в условиях однопроходной обработки (t = Δ).
Тогда целевая функция может быть представлена следующим образом:
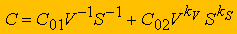 (3)
(3)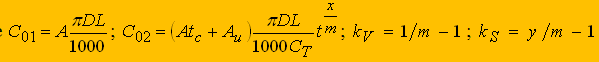
Для чистовой и тонкой токарной обработки необходимо учитывать ограничение по предельно допустимой шероховатость обработанной поверхности Ra:
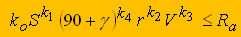 (4)
(4)Это ограничение необходимо представить в следующем виде:
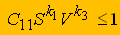 (5)
(5)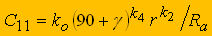
Математическая модель задачи оптимизации скорости резания и подачи при тонком точении представляется следующим образом:
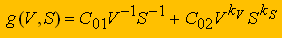 (6)
(6)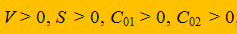
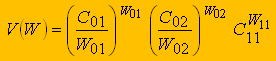 (7)
(7)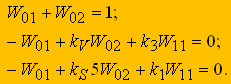 (8)
(8)
Согласно МГП на первом этапе оптимизации скорости резания и подачи решается система линейных уравнений (8), имеющая единственное решение:
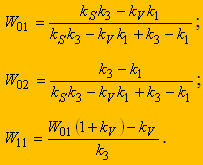 (9)
(9)Особенность МГП является возможность уже на первом этапе решения оценить вклад каждой составляющей целевой функции в общую себестоимость С - (3). Стоимость первой составляющей, связанной с машинной обработкой оценивается весомостью W01, а составляющей, связанной со сменой инструмента - W02.
Далее вычисляется экстремум целевой функции, для чего рассчитывается максимум двойственной функции V(W) - (7). На основании найденного экстремума целевой функции составляется система линейных уравнений для определения оптимальных режимов резания:
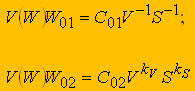 (10)
(10)В результате решения этой системы определяются оптимальные подача S0 и скорость резания V0:
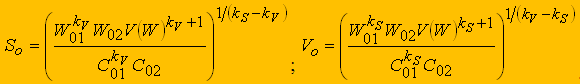 (11)
(11)Примеры определения оптимальных режимов резания, обеспечивающих минимальную себестоимость, приведены для токарной обработки вала (наружное продольное точение) диаметром D = 100мм, длиной L = 250мм из стали 45 на токарно-винторезном станке с ЧПУ 16К20Ф3. Для этих условий принято: себестоимость станко - минуты А = 0,5коп/мин., время смены инструмента tc = 1мин.
Для чистовой обработки используются сборные резцы с механическим креплением пластин из твердого сплава Т15K6 (передний угол γ= 0o, радиус при вершине r = 1мм); глубина резания t = 2мм; требуемая шероховатость обработанной поверхности Ra = 3,2мкм. Для указанных условий обработки принятые следующие коэффициенты и показатели, которые характеризуют степень влияния глубины, подачи и стойкости на скорость резания: CV =350, xv = 0,15, yv = 0,35, m = 0,2. Тогда CТ = 525•1010, kV = 4, kS = 0,75 [4].
Коэффициенты и показатели, которые характеризуют степень влияния подачи, переднего угла, радиуса при вершине и скорости резания на шероховатость обработанной поверхности: k0 = 7,0; k1 = 0,85; k2 = -0,65; k3 = -0,36; k4 = 0,15 [5].

Представленные на рис.1 графики свидетельствуют о том, что оптимальная подача SО увеличивается с увеличением шероховатости поверхности Ra и радиуса при вершине r; оптимальная скорость резания VО увеличивается с увеличением радиуса при вершине r и уменьшается с увеличением шероховатости поверхности Ra.
Расчетные значения коэффициентов С01 = 392,7, СО2 = 1,257•10-10, С11 = 4,296. Коэффициенты весомостей, определенные в соответствие с формулой (9), равны: W01 = 0,752, W02 = 0,248, W11 = 0,666.
Оптимальные значения подачи и скорости резания, рассчитанные в соответствие с формулами (11) и (12) равны: SО = 0,216 мм/об, VО = 209 м/мин.
Для тонкого точения используются резцы, оснащенные эльбором (передний угол γ = 0o, радиус при вершине r = 0,5мм); глубина резания t = 0,5мм; требуемая шероховатость поверхности Ra = 0,8 мкм. Для указанных условий обработки принятые следующие коэффициенты и показатели: CТ = 52,6•104, kV = 0,65, kS = -0,5 [6].
Коэффициенты и показатели, которые характеризуют степень влияния подачи, переднего угла, радиуса при вершине и скорости резания на шероховатость обработанной поверхности: k0 = 0,16; k1 = 0,59; k2 = -0,29; k3 = -0,19; k4 = 0,66 [5].
Расчетные значения коэффициентов С01 = 392,7, СО2 = 1,257•10-10, С11 = 4,766. Коэффициенты весомостей, определенные в соответствие с формулой (9), равны: W01 = 0,27; W02 = 0,73, W11 = 1,076.
Оптимальные значения подачи и скорости резания, рассчитанные в соответствие с формулами (11) и (12) равны:: SО = 0,116 мм/об, VО = 145 м/мин.
Для тонкого точения, также как и для чистового, оптимальная подача SО увеличивается с увеличением шероховатости поверхности Ra и радиуса при вершине r; оптимальная скорость резания VО увеличивается с увеличением радиуса при вершине r и уменьшается с увеличением шероховатости поверхности Ra (рис.2).
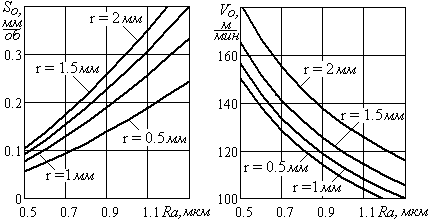
Из анализа установленных закономерностей изменения оптимальных режимов следует, что большие значения скорости резания и подачи для заданного уровня шероховатости могут быть приняты для больших радиусов при вершине, что при минимальной себестоимости обработки будет обеспечивать более высокую производительность.
Наличие аналитических зависимостей для определения оптимальных режимов резания существенно упрощает разработку рекомендаций по выбору рациональных условий обработки, что особенно актуально для чистового и тонкого точения.
Таким образом, представленная методика позволяет для любых условий чистового и тонкого точения выполнять расчеты оптимальных режимов резания, обеспечивающих минимальную себестоимость обработки.
С использованием МГП аналитически определены оптимальные режимы резания, обеспечивающие минимальную себестоимость обработки при заданном уровне качества обработанной поверхности при чистовом и тонком точении.
На основании разработанной методики установлены закономерности изменения оптимальных значений подачи и скорости резания от шероховатости обработанной поверхности и радиусов при вершине.
Разработанная методика определения оптимальных режимов резания может быть широко использована для любых видов обработки.