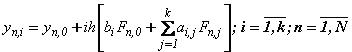Изоэффективный анализ параллельных методов решения задачи Коши на основе явных одношаговых методов

Автор: Назарова И.А., Фельдман Л.П.

Источник: Наукові праці Донецького національного технічного університету. Серія "Інформатика, кібернетика та обчислювальна техніка" (ІКОТ - 2009). Випуск 10 (153) - Донецьк: ДонНТУ. - 2009. - 316 с., 21-26 с.

В докладе представлены параллельные неявные многоточечные методы решения нелинейной задачи Коши с контролем погрешности на шаге и схемы их отображения на параллельные вычислительные структуры топологий гиперкуб, 2D-решетка/тор и линейка/кольцо. Данные методы обладают высокой устойчивостью и являются изначально параллельными, так как позволяют получать решение одновременно в нескольких точках сетки интегрирования.

Множество точек равномерной сетки : разбивается на N блоков [1]. Каждый блок содержит k точек и при этом N?M. Предполагается, что в пределах блока все точки равноудалены друг от друга:

где номер точки в блоке, ; n - номер блока, ; - точка с номером i, принадлежащая блоку n; - начальная точка n-го блока; – конечная точка n-го блока. Множество точек n-го блока из k точек обозначается . При этом имеет место равенство: (рис. 1).

Уравнения одношаговых блочных разностных методов в применении к ОДУ для блока из точек могут быть записаны в виде:

Разложением в ряд Тейлора входящих в невязку функций можно показать, что одношаговый k-точечный блочный метод имеет наивысший порядок аппроксимации, равный , следовательно, локальная ошибка в узлах блока имеет порядок . Блочные параллельные методы относятся к классу неявных, поэтому для вычисления приближенных значений решения задачи Коши необходимо разрешить систему нелинейных уравнений. Одним из способов получения решения является метод простой функциональной итерации:

где n – номер блока, n = 1,2,…,N; i – номер точки блока, ; l – номер текущей итерации ; L - максимальное число ненулевых итераций.

В отличие от явных методов решения СОДУ, реализация альтернативных способов оценки апостериорной локальной погрешности на основе блочных методов связана с рядом особенностей:

нет соответствующих последовательных аналогов, следовательно, требуется разработать и обосновать метод оценки локальной погрешности;
варьирование шага интегрирования возможно только после вычисления всех значений в k узлах текущего n-го блока
при условии неудовлетворительной оценки локальной погрешности практически все вычисления для точек блока окажутся напрасными (некоторые обращения к правой части могут быть использованы вновь).

Так, идея вложенных форм, предложенная для оценки локальной погрешности численного решения обыкновенных дифференциальных уравнений методами типа Рунге-Кутты, может быть использована и для одношаговых блочных многоточечных методов на основе двух различных подходов:

комбинация независимых формул разных порядков точности
комбинация специально подобранных формул разных порядков точности

подход заключается в применении двух различных независимых блочных методов смежных порядков точности на одной и той же сетке интегрирования . При этом первый метод определяет аппроксимацию решения на основе -точечного одношагового метода, а второй - точечного, также одношагового метода. Второе приближенное решение в совпадающих узлах блоков и сетки используется для оценки апостериорной локальной погрешности. Второй подход к разработке блочных вложенных методов предполагает использование идеи последовательного повышения порядка точности [2] имеет своей целью сокращение вычислительных затрат на основе комбинации специально подобранных формул разных порядков. На основе численного эксперимента можно сделать вывод, что из двух рассмотренных методов вложенных форм для блочных одношаговых способов решения нелинейной задачи Коши для ОДУ, второй метод обладает несомненными преимуществами (см. рис. 2).

Для получения высокоточного решения на основе блочных методов предложены алгоритмы, использующие технологию локальной экстраполяции. Разработанные вычислительные схемы параллельных блочных методов для одного дифференциального уравнения обобщены на системы дифференциальных уравнений. Тогда, кроме параллелизма метода используется и системный параллелизм, который, как правило, значительно больше. В перспективе предполагается провести сравнительный анализ с полностью неявными методами типа Рунге-Кутты, которые имеют аналогичную область применения, а именно жесткие задачи.

Литература

Worland P.B. Parallel methods for the numerical solution of ordinary differential equations // IEEE Trans. Comp. C. – 25, 10(1976). – P.1045-1048.
Крылов В.И., В.В. Бобков В.В., Монастырский П.И. Вычислительные методы, том I. – М.: Наука, 1976. – 303с.