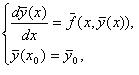Экстраполяционные одношаговые параллельные методы решения систем обыкновенных дифференциальных уравнений

Автор: Иванов А.В., Назарова И.А., Фельдман Л.П.

Источник: Материіали I всеукраїнської науково-технічної конференції студентів, аспірантів та молодих вчених – 19-21 травня 2010р., Донецьк, ДонНТУ. – 2010. – с. 202-205.

Общая постановка проблемы

Системы обыкновенных дифференциальных уравнений (СОДУ) большой размерности являются важнейшим инструментом для описания множества явлений и процессов различной природы. Высокая вычислительная сложность численного решения многомерных начальных задач требует построения эффективных параллельных алгоритмов для интегрирования таких систем.

Постановка задачи исследования

Современный эффективный алгоритм численного решения задачи Коши для СОДУ должен содержать механизм управления шагом интегрирования на основе информации о локальной апостериорной погрешности. Одним из известных способов оценки шаговой погрешности является технология локальной экстраполяции, обладающая высокой степенью внутреннего параллелизма, а, следовательно, преимуществами при реализации на параллельных компьютерах. Целью данной работы является разработка и анализ эффективности параллельных экстраполяционных одношаговых методов, а также программная реализация разработанных приложений.

Решение задачи и результаты исследований

Метод локальной экстраполяции Ричардсона (ЛЭР) является обобщением технологии удвоения шага по правилу Рунге [1-2]. Идея метода заключается в многократном измельчении шага интегрирования, и также в многократном применении процесса вычисления – локальная экстраполяция (рис. 1).

Рис.1 – Технология локальной экстраполяции

Решение задачи Коши для систем обыкновенных дифференциальных уравнений первого порядка

рассматривается при переходе из точки в точку , где H – базовая длина шага. Выбирается ряд натуральных чисел такой, что: и, соответственно, последовательность шагов интегрирования: , где . Задается опорный численный метод порядка и, вычисляется приближенное решение исходной задачи: . Выполнив вычисления для ряда последовательных значений i, по рекуррентному соотношению (2), определяют – экстраполированные значения для произвольных i, j (рис. 2). Процесс вычисления по (2) получил название полиномиальная экстраполяция Эйткена-Невилла [1-3]:

Здесь величина b равна единице в общем случае, в тоже время для симметричных опорных методов b равно двум.

Рис.2 – Вычисления по схеме полиномиальной экстраполяции, при k=4

На рисунке (3) – есть приближенное решение задачи Коши, полученное численным методом порядка с шагом . Экстраполяционные методы имеют то преимущество, что у них на каждом шаге можно менять не только длину шага, но и порядок метода. Следовательно, экстраполяцию можно рассматривать как метод с переменным порядком (столбцы таблицы) и переменным шагом интегрирования (строки таблицы).

Построим эффективный с точки зрения минимизации вычислительных затрат последовательный метод с использованием технологии Ричардсона.

Экстраполяционная технология включает:

опорный численный метод решения задачи Коши,
последовательность сеток,
рекуррентное правило вычисления значений приближенного решения.

Эффективность применения ЛЭР напрямую зависит от правильного выбора и сочетания всех трех составляющих. В качестве опорного метода был выбран метод Рунге-Кутта 4-го порядка. Данный метод является симметричным. Это значит, что он имеет асимптотическое разложение по степеням , и каждая экстраполяция исключает две степени . Тогда, количество строк экстраполяционной таблицы, определяется из следующего соотношения:

Рис.3 – Экстраполяционная таблица

Следовательно, если вычислены k строк экстраполяционной таблицы, то для симметричных опорных методов имеем в качестве аппроксимации наивысшего порядка точности, равного 2k, при этом точность аппроксимации составит – ( ). Для получения множества шагов интегрирования используется числовая последовательность: P={1,2,4,6,8,10,12,...}, воспользоваться свойством симметричности [3].

Потенциально вычисления по технологии локальной экстраполяции содержат три источника внутреннего параллелизма:

системный параллелизм (ограничен размерностью СОДУ, m);
параллелизм экстраполяции (ограничен размерностью таблицы экстраполяции, k);
параллелизм опорного метода (малая степень параллелизма).

Поскольку в основу вычислений положена явная численная схема, реально имеется возможность использовать системный и экстраполяционный параллелизм. В качестве способа соединения процессоров выбрана топология “звезда”.

Общая схема алгоритма локальной экстраполяции:

определяется размерность экстраполяционной таблицы на основе требуемого порядка экстраполяционного метода;
в соответствии с используемым типом параллелизма распределяются данные между процессорами;
вычисляется начальное приближение, на основе опорного метода (первый столбец экстраполяционной таблицы);
вычисляются значения экстраполяционной таблицы по формуле Эйткена-Невилла;
выполняются необходимые пересылки данных между процессорами через управляющий процессор в силу особенностей выбранной топологии.

Для разработки параллельных алгоритмов и оценки их эффективности использовалась поэтапная декомпозиционная методика, включающая применение графов влияния на разных уровнях детализации [4]. Определение теоретических характеристик параллелизма выполнялось с помощью пакета Mathematica? (Wolfram Research Inc.). Тестирование параллельных приложений производилось средствами библиотеки MPICH-2.2 для OS Windows.

На основе полученных данных построены зависимости ускорения и эффективности от размерности СОДУ и длины экстраполяционной таблицы (рис. 4).

Рис.4 – График характеристики ускорения для различных типов распараллеливания

Данный график позволяет сделать вывод об эффективности методов распараллеливания. Однако поскольку опыты проводились на системах небольшой размерности, а именно 2, 4, 6, 8, 10 уравнений, то значительную часть времени занимает пересылка сообщений между процессорами. Поэтому для получения более точных результатов необходимо провести ряд опытов на системах большой размерности.

Выводы

Сравнительный анализ динамических характеристик параллельных алгоритмов локальной экстраполяции на основе явных методов Рунге-Кутты показал, что областью приложений ЛЭР является высокоточное решение, сложная правая часть и многомерные задачи, однако требуется тщательный учет всех составляющих параллельной системы для того, чтобы такое решение было эффективным. В дальнейшем планируется расширить исследования за счет использования разных топологий, варьирования числовых последовательностей для генерации сеток интегрирования, а также применения неявных опорных методов, пригодных для решения жестких задач. Полученные результаты будут использованы при разработке библиотеки параллельного численного анализа для кластера WCCS-2003 Донецкого национального технического университета.

Список литературы

Хайрер Э., Нерсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи.– М.: Мир, 1990. – 512с.
Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи: Пер. с англ. – М.: Мир, 1999. – 685с.
Холл Дж., Уатт Дж. Современные численные методы решения обыкновенных дифференциальных уравнений. – М.: Мир, 1999. – 311с.
Фельдман Л.П., Назарова И.А. Эффективность параллельных алгоритмов оценки локальной апостериорной погрешности для численного решения задачи Коши // Электронное моделирование, т. 29, № 3, 2007. - С.11-25.